Метод дискретных направлений в нелинейной задаче фитирования спектров некогерентного рассеяния

Определение параметров ионосферной плазмы по экспериментальным спектрам некогерентного рассеяния (НР) является некорректной обратной задачей, в которой искомые параметры входят нелинейным образом в выражение для теоретического спектра мощности [Faley, 1966]. Для задач такого типа используют численные методы решения – прямой расчет набора модельных спектров и выбор среди модельных спектров наиболее близкого к экспериментальному спектру. Такая процедура является стандартной в подобного рода задачах и называется фитированием, т. е. подгонкой модельной функции к экспериментальной. Спектры некогерентного рассеяния должны рассчитываться для разных значений электронной и ионной температур Т е , T i , относительной концентрации ионов атомарного кислорода N O + и скорости дрейфа плазмы вдоль луча зрения радара V_d . На начальном этапе исследований методом НР [Hagen, Hsu, 1974] в алгоритме фитирования использовалась библиотека таких модельных спектров, и экспериментальный спектр сравнивался с заранее рассчитанными библиотечными спектрами. Очевидно, такая библиотека требовала большой оперативной памяти компьютера и на тот момент не могла обеспечить достаточного мелкого шага поиска. С увеличением быстродействия компьютеров стало возможным [Swartz, 1978] рассчитывать модельные спектры непосредственно перед сравнением их с экспериментальным и выбирать произвольный шаг поиска. Для проведения фитирования обычно использовался один из методов, описанных в работах [Bard, 1970; Dennis, et al., 1983], основанных на использовании частных производных спектра мощности по каждому из искомых параметров, а производные, если это было возможно, упрощались аналитически, что позволяло ускорить вычисления. Экспериментальный спектр мощности представляет собой дискретный набор из N отсчетов с известным шагом по частоте. Для возможности сравнения отсчеты модельного спектра вычисляются в тех же точках частотного диапазона.

Развитие технологии фитирования в методе НР в последние десятилетия проводилось в двух направ- лениях. Первое – это улучшение качества статистических оценок при зондировании кодированными последовательностями импульсов на основе традиционных алгоритмов [Vallinkoski, 1988; Lehtinen, Huuskonen, 1996]. Используемые здесь классические методы минимизации до настоящего времени являются единственными алгоритмами, работающими в реальном масштабе времени. Второе направление – это оптимальный анализ [Holt, et al., 1992; Nikoukar, et al., 2008], при котором функционал невязки вычисляется не для отдельных точек пространства, а целиком для профилей температуры ионов и электронов, и далее производится минимизация этого функционала. Такой подход является более точным, поскольку позволяет устранить неоднозначности интерпретации спектров, вызванные одновременным изменением газового состава и температуры, которые приводят к одинаковым изменениям формы спектра [Erickson, 1998]. Однако время работы таких алгоритмов настолько велико, что в 90-х годах обработка часового эксперимента требовала более суток вычислений [Holt, et al., 1992], и даже при использовании современных вычислительных средств [Nikoukar, et al., 2008] работа этих алгоритмов в масштабе реального времени проблематична.

Описанный в настоящей работе алгоритм предназначен для классической обработки данных НР в реальном масштабе времени и должен обеспечить работу в условиях низкого отношения сигнал/шум (S/N). Причиной низкого отношения S/N для Иркутского радара НР являются два фактора. Во-первых, его частотный диапазон (~160 МГц) обладает относительно высоким уровнем естественных радиошумов. Во-вторых, для волноводно-щелевых антенн характерно наличие случайных искажений спектров в присутствии резких градиентов электронной концентрации. Суть этих искажений состоит в том, что для волноводно-щелевой антенны Иркутского радара НР изменение частоты принимаемого сигнала в полосе приема 10–15 кГц эквивалентно эффективному изменению угла наклона приемного луча на 0.05-0.08° (приблизительно 7-10 % от ширины луча). Это значит, что разные части спектра НР измеряются при разных углах наклона луча, и в присут- ствии значительных градиентов электронной концентрации спектр имеет характерную асимметрию, зависящую от знака градиента, поэтому основным требованием к алгоритму фитирования является его устойчивость к таким нестационарным шумам эксперимента.

Нелинейная задача о наименьших квадратах

Нелинейная задача о наименьших квадратах обычно возникает в приложениях, связанных с наилучшим приближением данных, где стараются наилучшим образом приблизить данные S(ωi) с помощью модели S(xk, ωi), которая нелинейна по x. С математической точки зрения задача фитирования есть поиск глобального минимума многомерного функционала невязки minФ(X1,x2...X—) = £(S(4.)-S(toi,X1,x2...X—))2, (1)

^{X 5} R i = 1

где S – экспериментальный спектр, S – модельный спектр, x k – набор параметров, по которым проводится минимизация, ω _i – сетка частот, m – число фитируемых параметров.

Поскольку в эксперименте присутствуют шумы, для описания экспериментальных данных часто используют статистические методы, считая экспериментальную функцию случайным процессом с нормальным законом распределения [Bard, 1970; Dennis, et al., 1983; Lehtinen, Huuskonen, 1996]. На основе центральной предельной теоремы опреде-ляяются вероятностная оценка среднего значения случайного процесса и его дисперсия. В таком подходе ищется минимум распределения:

A x² = 1. (3)

Иными словами, доверительной областью значений полученных параметров x k с заданной вероятностью будет кривая на поверхности χ², где значение невязки равно 2σ. Именно из статистических соображений в качестве меры для наилучшего приближения данных используют квадрат отклонения, для которого статистическая теория разработана лучше [Bard, 1970].

Основной задачей при обработке спектров некогерентного рассеяния является поиск электронной и ионной температур, от которых спектр сигнала зависит нелинейно, поэтому в первую очередь мы рассмотрим двухпараметрический функционал невязки Ф( T e , T i ). На рис. 1 приведены примеры функционалов невязки для реальных спектров, измеренных на радаре НР ИСЗФ [Жеребцов и др., 2002; Shpynev, 2004]. В данных примерах глобальный минимум очевиден, хотя доверительная область, описываемая второй от минимума изолинией, имеет несимметричный вид, характеризующий наиболее вероятные ошибки изме-

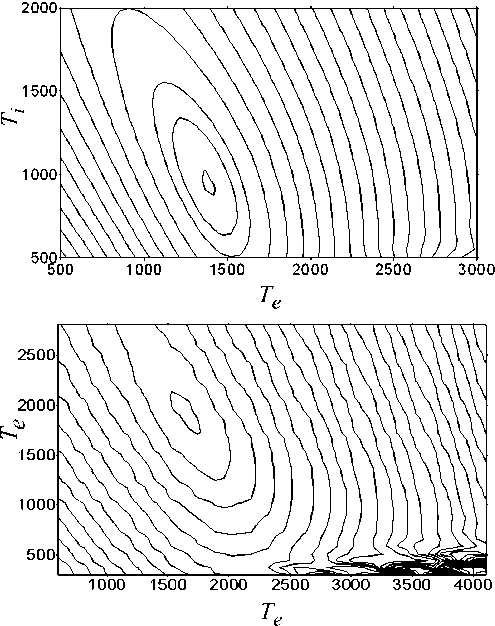
Рис. 1. Изолинии проведены с шагом, равным диспер- сии σ.

рений. На функционале, изображенном в нижней части рис. 1, положение глобального минимума не соответствует физической реальности T_e < T_i , и требуется привлечение дополнительных физических условий для корректного решения данной задачи. Большая протяженность доверительной области на функционалах (рис. 1) является следствием упомянутых выше больших шумов эксперимента.

В литературе [Dennis, et al., 1983, Hamming, 1972] рассмотрен ряд методов поиска решения нелинейной задачи о наименьших квадратах. Наиболее распространенными являются методы Ньютона, Гаусса– Ньютона, метод секущих и их вариации [Dennis, et al., 1983]. Основа этих методов состоит в определении первых частных производных от Ф( x 1 , x 2 , …, x m ) по каждому из параметров, построение линейной модели Ф( x ₁, x ₂, …, x _m) в окрестности текущей точки и спуск в направлении глобального минимума функционала. Иногда для оценки вклада вторых производных необходимо пользоваться квадратичной моделью функционала, что требует вычисления вторых производных по каждому из параметров.

Данные методы обладают хорошей локальной сходимостью для задач, которые не являются слишком нелинейными или имеют в решении достаточно малые невязки. Напротив, для задач, которые слишком нелинейны или имеют в решении достаточно большие невязки, методы не обладают локальной сходимостью и не гарантируют глобальную сходимость. Необходимость вычисления производных по параметрам xi является существенным недостатком данных методов, поскольку часто требует применения конечных разностей порядка выше первого, а иногда и вычисления вторых производных, что ведет к дополнительным (m2+3m)/2 вычислениям функционала Ф(x1, x2, … xm) на каждой итерации. Поскольку модель S(ωi, x1, x2, … xm) обычно имеет довольно сложный вид [Шеффилд, 1978], такие затраты бывают непозволительными, и пользователям алгоритмов приходится прибегать к дополнительной информации для ускорения работы.

Еще одной общей проблемой для методов решения нелинейной задачи о наименьших квадратах является критерий останова алгоритма. Во-первых, ноль производной может означать как точку минимума, так и точку перегиба функционала, тогда для определения минимума нужен расчет вторых производных. Во-вторых, если вблизи глобального минимума Ф( x ₁, x ₂, … x _m) невязка остается достаточно большой, в классических методах тяжело выработать критерий останова, который удовлетворял бы требованиям точности, хотя такая ситуация часто встречается в реальных измерениях.

Опыт других авторов [Erickson, 1998] и проведенные нами исследования показали, что для глобальной сходимости алгоритмов решения нелинейной задачи о наименьших квадратах применительно к спектральным измерениям в методе НР одним из самых важных моментов является выбор начального приближения параметров задачи. В некоторых случаях, встречающихся на практике, функционал Ф( x 1 , x 2 , … x m ) имеет множественные локальные минимумы, а глобальный минимум иногда представляет собой желоб (набор решений задачи с одинаковой невязкой). Такая неоднозначность решения в задаче НР чаще всего вызвана наличием в плазме ионов разного сорта или неопределенностью в значении T e / T i , видимой как сильная вытянутость функционалов на рис. 1.

Для выбора единственного решения из возникающего множества (или корректировки данных) необходимо использовать дополнительную информацию. Так, в программе обработки данных радара Миллстон-Хилл [Erickson, 1998] использовалась информация о температурах с ближайших высот, и в функционал невязки вносится ограничение, изменяющее его в пользу наиболее вероятных температур. С учетом указанных проблем, возникающих при обработке экспериментальных данных в методе НР, нами был разработан метод фитирования спектров НР, хорошо сходящийся в различных шумовых условиях и позволяющий избежать некоторых проблем стандартных алгоритмов.

Метод дискретных направлений

В данном методе не проводятся вычисления производных по параметрам функционала Ф( x 1 , x 2 , … x m ) и используется фиксированный шаг при спуске к глобальному минимуму. Поскольку в реальных экспериментальных данных шумы не позволяют определять положение глобального минимума с произвольно заданной точностью, величину начального шага поиска неразумно делать меньше типичной ошибки измерений. Лишь при нахождении (приближенно) минимума Ф( x 1 , x 2 , … x m ) можно уменьшить шаг и определить минимум более точно. При последовательном проведении минимизации Ф( x 1 , x 2 , … x m ) на серии однотипных спектров шаг поиска для каждого последующего функционала невязки может быть определен из предшествующих расчетов.

Суть метода дискретных направлений (ДН) заключается в том, что вместо вычисления производных по каждому из параметров функционала Ф( x 1 , x 2 , … x m ) и построения его линейной модели использован поиск минимального значения функционала на окружностях с радиусами Δ x i , соответствующими шагу поиска по каждой из переменных.

Для наглядности рассмотрим работу метода на двухпараметрическом функционале Ф( x 1 , x 2 ) с одинаковым шагом Δ x . На каждой итерации будем вычислять значения функционала Ф( x 1 , x 2 ) в дискретном наборе k точек плоскости ( x ₁, x ₂), расположенных симметрично вдоль окружности с радиусом Δ x , причем отсчет углов будем производить от направления на точку предыдущей итерации или от нуля при первой итерации. Выбирая из k точек ту, в которой функционал Ф( x 1 , x 2 ) минимален, переместимся в нее и продолжим процесс вычисления по данной схеме, пока значение функционала в центральной точке окажется меньше, чем где-либо на окружности.

При минимальном значении k =3, которое может быть использовано в данном алгоритме, плоскость параметров ( x ₁, x ₂) разбивается на шестиугольники (рис. 2), количество необходимых вычислений Ф( x ₁, x ₂) равно k –1, т. е. двум (третья точка определяется на предыдущей итерации). Таким образом, по мере спуска от начального приближения Φ ( x ₁⁰ , x ₂⁰) к минимуму процесс поиска продвигается по ломаной, показанной на рисунке стрелками.

Только в трех случаях ( k =3; 4; 6) точки плоскости ( x 1 , x 2 ) лежат в узлах равномерной сетки из правильных шестиугольников ( k =3), четырехугольников ( k =4) и треугольников ( k =6). Для других значений k >3 периодическая сетка не существует.

Для выбора значения k , обеспечивающего максимальную скорость работы алгоритма, обратимся вновь к рис. 2. Пунктирная линия показывает возможные пути движения алгоритма при k =6. Как видно из рисунка, для спуска к минимуму, при k =3 алгоритму требуется восемь итераций и расчет 16 значений Ф( x 1 , x 2 ). При k =6 алгоритму потребуется семь итераций и расчет 35 значений Ф( x 1 , x 2 ). Быстродействие алгоритма с k =3 оказывается более чем в два раза выше. Можно показать, что быстродействие алгоритма при k =4 и при k =3 совпадает при движении по прямой вдоль одной из осей x 1 или x 2 , в остальных случаях быстродействие при k =3 будет выше, т. е. при k =3 данный алгоритм обладает максимальной скоростью.

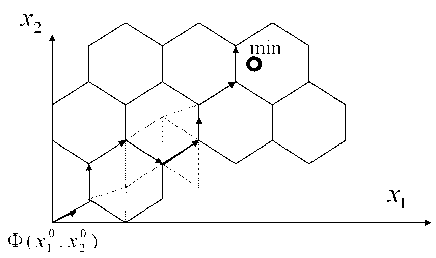
Рис . 2. Схема спуска в алгоритме дискретных направ лений .

Поскольку на каждой итерации при k =3 существует три возможных направления движения по плоскости ( x 1 , x 2 ), для каждого из этих направлений будет рассчитываться два значения функционала Ф( x 1 , x 2 ), третье значение известно из предыдущей итерации, и в любой итерации, кроме первой, оно больше текущего значения и может не рассматриваться.

Таким образом, в двумерном случае точка текущей итерации лежит в центре равнобедренного треугольника, а новые узлы являются его вершинами, которые можно определить, воспользовавшись тем, что равнобедренный треугольник является симплексом размерности 2. Пользуясь правилом построения симплекса размерности 2, поместим центр равнобедренного треугольника в начало координат, как это изображено на рис. 3, и положим длину его стороны Δ x =1.

Координаты вершин будут равны D(0,  3 /3 ),

B( - 1/2, - 73/6,) и C(1/2 - 73/6).

По мере движения алгоритма к точке с наименьшей невязкой центр треугольника перемещается в новую точку:

• 1)    при движении вверх вычисляются значения Ф( x i , x ₂) в точках ( x 1 - 1/2, x ₂ + 73/6) и ( x 1 + 1/2, x ₂ + V3 /6);

• 2)    при движении влево (вверх, вниз) – в точках ( x 1 , x ₂ ± 73/3) и ( x 1 - 1/2, x ₂ m 73/6);

• 3)    при движении вправо (вверх, вниз) – в точках ( x 1 , x ₂ ± 73/3) и ( x 1 + 1/2, x ₂ m 7376).

По аналогии можно построить правило расчета новых вершин для функционала типа Ф( x ₁, x ₂, x ₃). В этом случае новые точки будут вершинами симплекса размерности 3 – тетраэдра (рис. 4). Для построения общего правила определения координат узлов сетки, составленной из вершин симплексов, обратимся к рис. 5 и 6, которые описывают двумерный и трехмерный случай соответственно.

В двумерном случае (рис. 5) координаты новых узлов A1, B1, C1 определятся как отражение узлов A, B, C на предыдущей итерации относительно прямой

^

ОЕ, проведенной через середину вектора BB ¹ , проведенного из узла на предшествующей итерации в текущий узел. По условию построения, точки A, B¹, C являются вершинами равнобедренного треугольника, а точка B делит высоту MB¹ треугольника AB¹C в соотношении 1/2. Из рисунка видно, что для нахождения координат новых узлов необходимо к координатам узлов на предыдущей итерации доба- ^

вить вектор BB ¹ , умноженный на два.

В трехмерном случае (рис. 6) новые узлы находятся путем отражения старых узлов относительно плос- ^ кости, проходящей через середину вектора BB ¹ и перпендикулярной ему. Преобразования координат узлов будут представлять собой параллельный пе- ^

ренос на вектор BB ¹ с коэффициентом 5/3, равным отношению высоты тетраэдра к расстоянию от вершины до центра.

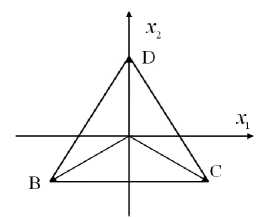
Рис . 3. Относительные координаты вершин равнобед ренного треугольника на плоскости .

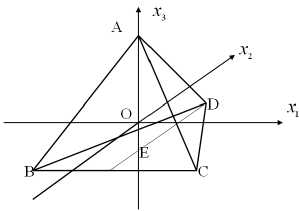
Рис . 4. Относительные координаты вершин тетраэдра в трехмерном пространстве .

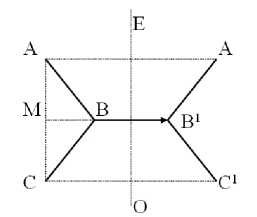
Рис . 5. Схема построения узлов сетки на плоскости .

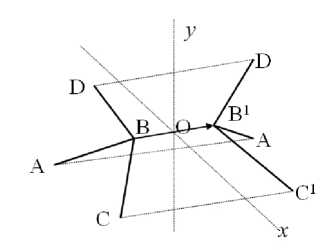
Рис . 6. Схема построения узлов сетки в объеме .

Данный метод можно обобщить на случай симплекса произвольной размерности порядка n , где n >1. При этом правильный ( n +1)-угольник (симплекс) строится из симплекса размерности n –1 по следующему алгоритму:

• 1)    рассчитывается длина высоты h n нового симплекса по формуле h n = 71 - h n - 1 , где h n - 1 - высота симплекса размерности n –1;

h

• 2)    симплекс размерности n -1 сдвигается на —- n вдоль новой переменной x n ;

• 3)    добавляется новая точка с координатами (0,0,0,...,1 - h^- ).

n

После построения симплекса размерности n определяются координаты вершин симплекса и ищется вершина с наименьшей невязкой. Строится вектор K из текущей точки в направлении точки наименьшей невязки, и координаты векторов A_; ( x 1 ,x 2 ,....,x n ) ( i = 1,..., n- 1) узлов в новой итерации определяются по формуле

—             n + 2 r

A i ( x 1 , x 2 ,...., x n ) = A i ( x 1 , x 2 ,...., x n ) +------ K ,      (4)

n где Ai (x1 , x2,...., xn ) – текущие координаты вершин симплекса.

Алгоритм ДН останавливается , если значение функционала в текущей точке ( в центре симплекса ) меньше , чем в какой - либо из вершин .

Поскольку сетка узлов является равномерной по всем переменным , при использовании метода на практике необходимо проводить соответствующее масштабирование , чтобы скорость движения по ка ждой из переменных соответствовала реально полу чаемой точности и диапазону изменения параметра .

Тестирование

Для двумерного функционала невязки метод ДН сравнивался с классическим алгоритмом градиентного спуска на одинаковом массиве теоретических и экспе риментальных спектров , соответствующих разным ионосферным условиям и разным отношениям сиг - нал / шум . При аппроксимации теоретических спектров мощности более высокую точность давал классиче ский алгоритм c приблизительно равной скоростью расчета . При обработке экспериментальных спектров алгоритмы давали одинаковые в пределах точности измерений результаты при S/N>1, а скорость работы алгоритма ДН была в 1.6–2.1 раза выше . При 0.1 новый алгоритм работал в среднем в 2–3 раза быстрее, причем классический алгоритм в нескольких случаях выходил из области анализа.

Алгоритм дискретных направлений тестировался также на функционалах с размерностью 3 и 4. Для функционала ФСГ, T, N _{O +} ) он также дает хорошую устойчивость и скорость работы и используется в настоящее время при регулярной обработке спек тров НР . При размерности 4 для функционала типа Ф ( Т_е , Т , N _{о +} , V d ) точность фитирования ухудшается ввиду упомянутых выше искажений спектра , де лающих задачу неоднозначной . Поэтому определе ние скорости дрейфа V d проводится нами по допле ровскому сдвигу частоты вне основного цикла фи - тирования . Возможно , в задачах , где функционал невязки не является сильно нелинейным , алгоритм ДН будет устойчив и для больших размерностей функционала невязки , однако такое тестирование в данной работе не проводилось и не предполагалось .

Выводы

Предложенный метод фитирования показал себя более эффективным по сравнению с традиционными в нелинейной обратной задаче в присутствии шумов. Он требует только n вычислений функционала невязки на каждой итерации (в сравнении с 2*n вычислений в методах, использующих первые частные производ- ные). Последовательное применение метода с разным значением шага сетки позволяет обеспечить необходимую точность, а возможность работы с большим шагом позволяет достаточно быстро проводить поиск глобального минимума на всей поверхности для функционалов, являющихся слишком нелинейными и имеющих большую невязку. Важным преимуществом нового алгоритма является простота и однозначность критерия останова, что обычно представляет определенную проблему в классических алгоритмах.

Описанный метод фитирования реализован в рамках комплекса вторичной обработки спектров мощности радара НР ИСЗФ . Высокая скорость ра боты и гибкость алгоритма в выборе шага сетки по зволяет проводить повторные или последовательные итерации поиска решения задачи минимизации (1) и эффективно корректировать точность фитирования . Для программирования алгоритм удобен , так как обладает простотой и единообразием построения симплексов высших порядков .

Работа выполнена при поддержке гранта РФФИ № 08-05-00618- а .