Метод главного фактора в оценке машин и оборудования

В конце 1990-х годов В. Быковой был предложен метод направленных корректировок для оценки машин и оборудования (далее – машины). В 2000 году он был изложен в работах [1, 2], а позднее – в ряде учебников и учебных пособий (см. [3–6]). Этот метод предназначен для оценки машин в ситуациях, когда известно много характеристик машины и ее аналогов, но неизвестно, как именно каждая из них влияет на стоимость. При применении этого метода предполагается, что различия в степени износа машины и аналогов учитываются отдельно, так что, по существу, этот метод ориентирован на оценку восстановительной стоимости (далее – ВС) машины по данным о ВС ее аналогов.

Суть метода продемонстрируем на простом примере, приведенном в работе [4]. Единицы измерения стоимости машин здесь и далее не указываются.

Пример 1

Оценивается стоимость пилорамы КРС75 (далее – машина М0) по данным ее «нижнего» и «верхнего» аналогов – пилорам РК63-2 и Р80-2 (далее – машины М1 и М2). Значения характеристик машин приведены в таблице 1 (в работе [4] – таблица 4.7). Предполагается, что увеличение значения любой характеристики повышает потребительские свойства машины и, следовательно, увеличивает ее стоимость.

Таблица 1

Значения характеристик оцениваемой машины и ее аналогов

Характеристика	Обозначение характеристики	Машина
		М0	М1	М2
Ширина просвета пильной рамки, мм	X 1	750	630	800
Ход пильной рамки, мм	X 2	360	400	500
Частота вращения главного вала, об/мин	X 3	285	285	250
Наибольшая длина распиливаемых бревен, м	X 4	7,5	7,5	10
Наибольшая подача на 1 оборот главного вала, мм	X 5	26	22	40
Наибольшее число пил в поставе	X 6	12	12	14
Мощность электродвигателей, кВт	X 7	52,4	44,4	64
Производительность, м3/ч	X 8	4	5	9
Стоимость	V	–	415,3	590,8

Суть метода состоит в подсчете количества повышающих и понижающих корректировок, которые необходимо внести в стоимости аналогов для получения искомой оценки.

Из таблицы 1 видно, что для «приведения» машины М1 («нижний» аналог) к М0 необходимо увеличить три характеристики ( X ₁, X ₅ и X ₇) и уменьшить две ( X ₂ и X ₈). Это позволяет (см. [1, 2]) определить количество «действующих повышающих корректировок»: 3 – 2 = 1. Точно так же, чтобы «привести» машину М2 («верхний» аналог) к М0, необходимо уменьшить семь характеристик ( X ₁, X ₂, X ₄, X ₅, X ₆, X ₇ и X ₈) и увеличить одну ( X ₃). Таким образом, здесь количество «действующих понижающих корректировок» составит: 7 – 1 = 6. На этом основании предлагается оценить стоимость V ₀ машины М0 как средневзвешенную из стоимостей машин М1 и М2, приняв в качестве весов указанные количества действующих корректировок в обратном порядке (то есть аналогу с меньшим количеством корректировок приписывается больший вес). В результате находим:

V 0 = (415 , 3 X 6 + 590 , 8 X 1) / (6 + 1) = 440 , 4.

В работах [2–4] этот метод обобщен на случай, когда имеются более двух аналогов и отдельным характеристикам можно придавать различные веса, однако мы пока не будем на этом останавливаться.

К преимуществам рассматриваемого метода, безусловно, следует отнести то, что для его применения не требуется информация о «степени влияния» отдельных характеристик на стоимость машины. Однако он имеет и недостатки, а именно:

• 1)    считается, что все характеристики влияют на стоимость машины примерно одинаково – на результат расчета влияет только количество отличающихся в ту или другую сторону характеристик машины и ее аналога. Поэтому в примере 1 результат не изменился бы, если у оцениваемой машины были бы, например, такие характеристики: X ₂ = 400, но X ₃ = 275;

• 2)    результат оценки не меняется, как бы ни менялись значения характеристик оцениваемой машины (и ее аналогов) в определенных интервалах. Так, в примере 1 результат оценки стоимости машины будет одним и тем же при любом значении X ₅ в пределах от 23 до 39;

• 3)    результат оценки меняется скачком , как только значения какой-либо характеристики у машины и ее аналога сравняются. Например, если бы у машины М0 значение X ₃ оказалось чуть меньше (скажем, 284 вместо 285), то результат оценки сразу уменьшился бы с 440 , 4 до 415 , 3. Другими словами, этот метод не обеспечивает непрерывную зависимость стоимости машины от значений ее характеристик;

• 4)    при наличии более двух аналогов возникают проблемы при выборе «нижнего» и «верхнего» аналогов. Их можно преодолеть, вводя дополнительные допущения, не связанные с сутью рассматриваемого метода.

Казалось бы, эти недостатки имеют формально-математической характер. Между тем они достаточно серьезные. Дело в том, что все характеристики машин взаимосвязаны. Об этом можно судить по коэффициентам корреляции между характеристиками машин из примера 1 (см. таблицу 2, в которой коэффициенты корреляции, превышающие 0 , 9, выделены жирным шрифтом).

Как видим, многие характеристики машин тесно связаны друг с другом. Так, высоким является коэффициент корреляции между X ₂ и X ₃ (-0,961). Тогда изменение X ₂, скорее всего, должно приводить к противоположному изменению X ₃. По этой причине повышающая корректировка стоимости М1 по характеристике X ₂ должна одновременно сопровождаться понижающей корректировкой этой стоимости по характеристике X ₃, что в рассматри-

Таблица 2

Коэффициенты парных корреляций между характеристиками машин

X1 X2 X3 X4 X5 X6 X7 X8 X1 1,000 0,508 -0,727 0,727 0,856 0,727 0,943 0,584 X2 0,508 1,000 -0,961 0,961 0,880 0,961 0,765 0,996 X3 -0,727 -0,961 1,000 -1,000 -0,977 -1,000 -0,914 -0,982 X4 0,727 0,961 -1,000 1,000 0,977 1,000 0,914 0,982 X5 0,856 0,880 -0,977 0,977 1,000 0,977 0,979 0,920 X6 0,727 0,961 -1,000 1,000 0,977 1,000 0,914 0,982 X7 0,943 0,765 -0,914 0,914 0,979 0,914 1,000 0,821 X8 0,584 0,996 -0,982 0,982 0,920 0,982 0,821 1,000 ваемом методе не учтено. Далее, коэффициенты корреляции между характеристиками X3, X4 и X6 равны единице, так что соответствующие корректировки «дублируют друг друга». Допустим, что с учетом этого мы исключили из рассмотрения характеристики X4 и X6. Тогда, чтобы «привести» машину М2 («верхний аналог») к М0, необходимо будет уменьшить только пять характеристик (X1, X2, X5, X7 и X8) и увеличить одну (X3). Из-за этого количество «действующих понижающих корректировок» составит уже 5 – 1 = 4, а результат оценки стоимости машины М0 изменится и составит (415,3 х 4 + 590,8 х 1) / (4 + 1) = 450,4. Конечно, такое изменение невелико, однако настораживает сам факт того, что устранение «дублирующих» характеристик влияет на результат оценки (ведь в других ситуациях изменение может оказаться и бо́льшим).

Высокие корреляции между характеристиками машин не случайны и не обусловлены тем, что для оцениваемой машины выбраны всего два аналога. Они наблюдаются и при рассмотрении трех и большего числа машин разных видов. Дело в том, что при проектировании аналогичных машин обычно исходят из небольшого числа основных ее характеристик, рассчитывая на их основе все остальные.

Но в таком случае возникает задача найти какой-то «главный фактор», с которым все остальные характеристики были бы наиболее тесно связаны какой-то зависимостью, и выяснить, как он влияет на стоимость машин. Казалось бы, решение такой задачи очевидно – технические специалисты давно используют классификации машин по их главным параметрам . Более того, в работе [4, с. 142] прямо указано, что «основной технологический параметр для лесопильных рам – ширина просвета пильной рамки», то есть X ₁. Увы, именно эта характеристика связана с остальными не очень сильно, во всяком случае слабее, чем X ₇ или X ₈. Мало того, стоимость машины в оценке обычно связывается с ее производительностью (в нашем случае – X ₈). Это значит, что при решении поставленной задачи ориентироваться на «главные технические параметры» машин не стоило бы.

Другой подход к выбору «главного фактора» можно вывести из применяемых оценщиками регрессионных стоимостных моделей.

Так, в работе [4, с. 150] построена зависимость стоимости листогибочных кривошипных прессов от номинального усилия пресса ( X ₁, кН) и длины рабочего стола ( X ₂, мм):

V = 0,76 х X О ⁷³²⁶ х X ₂ ^{0 1822}

■

Отсюда сразу же следует, что в качестве «главного фактора» пресса можно было бы принять, например, Х 0 ^,732 6 х X 0 ^,182 2 . К такой степенной комбинации характеристик мы еще вернемся, а пока заметим, что какого-то «технического» смысла она не имеет, хотя и связана со стоимостью машин прямой пропорциональной зависимостью.

В нашем случае у машин 8 характеристик и, комбинируя их, можно сформировать много разных «главных факторов». Более того, разным комбинациям могут отвечать одинаковые значения «главного фактора». Так, два разных фактора F = 0,5 X ₁ + 4,5 X ₆ + 22 X ₈ и G = 0,124 X ₂ + 0,6776 X ₃ + 10,74 X ₅ для машин М0, М1, М2 принимают одни и те же значения – 517, 479 и 661, поэтому подбирать подходящие линейные (или еще какие-нибудь) комбинации характеристик нет необходимости, достаточно лишь подобрать их подходящие значения для каждой машины.

Таким образом, мы приходим к тому, что в примере 1 надо найти некий набор из трех чисел ( F ₀, F ₁, F ₂), который можно трактовать как значения некоего «главного фактора» у машин М0, М1, М2, не придавая этому фактору какой-либо «технический» смысл. Разумеется, этот «главный фактор» должен быть возможно более тесно связан со всеми характеристиками машин. Если бы речь шла о тесноте связи между двумя факторами, то ее мерой естественно было бы считать коэффициент корреляции. Так, тесноту связи между «главным фактором» и X ₅ можно было бы измерить коэффициентом корреляции между набором ( F ₀, F ₁, F ₂) и набором (26, 22, 40), стоящим в строке X ₅ таблицы 1. При этом тесной надо было бы считать связь, у которой коэффициент корреляции близок к 1 или к -1 (в первом случае связь будет положительной, во втором отрицательной). На этом основании тесноту связи лучше характеризовать коэффициентом детерминации , который в данном случае совпадает с квадратом коэффициента корреляции. Но в нашем примере характеристик у машин много (8), поэтому мерой тесноты соответствующих связей естественно принять сумму коэффициентов детерминации между набором ( F ₀, F ₁, F ₂) и всеми наборами, расположенными в строках X ₁– X ₈ таблицы 1. Это значит, что «главному фактору» должен отвечать такой набор ( F ₀, F ₁, F ₂), для которого сумма коэффициентов детерминации с наборами, расположенными в строках X ₁– X ₈ таблицы 1, будет наибольшей.

Эта задача давно известна в статистике. Она является первым шагом так называемого метода главных компонент (Principal Component Analysis), предложенного Карлом Пирсоном в 1901 году и применяемого для отыскания наиболее важных факторов, определяющих характеристики объектов (подробнее см., например, [7–10]). Для нашей цели важно, что искомый набор определяется не однозначно. Дело в том, что коэффициенты детерминации не изменятся, если все числа в наборе ( F ₀, F ₁, F ₂) умножить на какое-либо отличное от нуля число (то есть изменить «масштаб» фактора) или увеличить на одно и то же число (то есть изменить «начало отсчета» фактора). Поэтому достаточно отыскать такой «подходящий» набор ( F ₀, F ₁, F ₂), для которого среднее значение из величин F_i будет равно 0, а их дисперсия будет равна 1. Не будем пока останавливаться на методе решения этой задачи, а посмотрим, как использовать полученное решение для оценки стоимости машины М0.

Итак, предположим, что мы нашли «главный фактор», наиболее тесно связанный с характеристиками машин. Естественно считать, что этот фактор будет достаточно тесно связан и со стоимостью машин. В таком случае мы можем построить зависимость стоимости машин V от «главного фактора» F и с ее помощью установить, какая стоимость V ₀ отвечает значению F ₀ – значению «главного фактора» для машины М0.

В нашем примере зависимость V(F) предельно проста – это прямая линия, соединяющая точки (415,3, F1) и (590, F2). Тогда искомая стоимость V0 находится путем линейной интерполяции, причем коэффициент детерминации между набором (F0, F1, F2) и набором стоимостей машин (V0, 415,3, 590) будет точно равен 1. Отсюда сразу же следует, что нет необходимости вначале подбирать «подходящий» набор (F0, F1, F2), а затем рассчитывать стоимость V0 машины. Вместо этого можно сразу же искать все 4 неизвестные величины F0, F1, F2, V0 так, чтобы их среднее значение стало равным 0, их дисперсия равной 1, а сумма коэффициентов детерминации между набором (F0, F1, F2) и наборами всех характеристик машин (включая их стоимости!) оказалась максимальной. Такой метод оценки можно назвать методом главного фактора 1.

Подобные задачи хорошо решаются в электронных таблицах. На рисунке показано решение рассматриваемого примера.

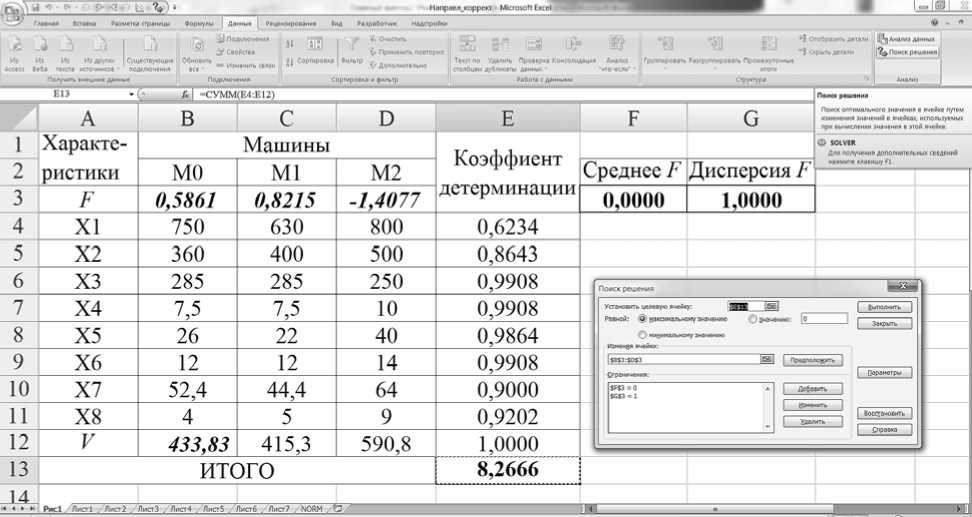
Рабочий лист Excel с расчетом стоимости машины

В ячейках B4–D12 записаны исходные данные (табл. 1), вместо стоимости машины в ячейке B12 проставляется любое число. Аналогично в ячейках B3–D3 проставляются любые числа. В ячейки F3 и G3 вставляются стандартные формулы для расчета среднего значения (функция СРЗНАЧ) и дисперсии (функция ДИСПР) из значений B3, С3 и D3. В ячейках Е4–Е12 вставляются формулы для расчета квадратов коэффициентов корреляции между набором (B3, С3, D3) и наборами, стоящими в тех же графах соответствующих строк таблицы (при этом используется стандартная функция КОРРЕЛ), в ячейке Е13 – сумма ячеек Е4–Е12. Затем используется опция «Поиск решения» (жирный знак вопроса со стрелкой). В раскрывающемся меню ставится задача: установить максимальное значение в ячейке Е13, изменяя ячейки B3–D3 и B12 (выделены жирным курсивом) при ограничениях F3 = 0 и G3 = 1. На рисунке показано полученное решение. Рассчитанная стоимость оцениваемой машины составила 433,83, что довольно близко к результату, полученному при применении метода направленных корректировок.

В изложенном виде метод главного фактора применим и при наличии трех или большего числа аналогов. Приведем подобный пример, построенный на данных примера 5.11 из работы [6].

Пример 2

Оценивается стоимость автоматической блочной котельной АМБК-0,4 (далее – М0) по данным о шести ее аналогах (с М1 по М6). Для характеристик машин используются следующие обозначения:

Характеристика	Обозначение характеристики
Мощность, МВт	X 1
КПД котлов	X 2
Отапливаемый объем, тыс. м3	X 3
Производительность, м3/ч	X 4
Давление газа, КПа	X 5
Потребление газа, м3/ч	X 6
Потребление электроэнергии, КВт/ч	X 7

Исходные данные и результаты расчетов в такой же, как на рисунке, форме представлены в таблице 3.

Таблица 3

Результаты оценки стоимости машины М0

Характеристика	Машина							Коэффициент детерминации
	М0	М1	М2	М3	М4	М5	М6
F	0,244	0,446	1,134	0,373	0,715	-0,924	-1,988
X 1	0,4	0,2	0,3	0,5	1,26	1,89	2,52	0,7283
X 2	0,91	0,91	0,91	0,91	0,92	0,92	0,92	0,3663
X 3	12	6	9	15	37,5	56,5	75,6	0,7313
X 4	3	0,5	1	3	5	9	12	0,8093
X 5	2,2	2,2	2,2	3,2	4,2	4,2	4,2	0,3620
X 6	48	24	36	61	152	228	304	0,7285
X 7	5,2	4	4.5	6.4	15	22.5	30	0,7422
V	2 336 , 5	1 043	1 248	2 086	2 970	4 076	5 404	0,7791
								5 , 2471

Таким образом, результат оценки стоимости машины М0 с использованием предложенного метода составляет 2 336 , 5 (в работе [6] результат оценки иной – 2 433 , 7). Эту оценку мы прокомментируем позднее, а пока отметим, что в ней отражено и влияние неучтенных непосредственно (случайных) факторов, поскольку коэффициент детерминации между главным фактором и стоимостью 0 , 7791 < 1.

Как видим, применение метода главного фактора дает разумные результаты. В отличие от метода направленных корректировок он не предполагает возрастающую зависимость стоимости машины от ее характеристик и учитывает вероятностный характер взаимосвязей между характеристиками. Его можно использовать, когда количество аналогов отно- сительно мало и построить надежную регрессионную зависимость стоимости машины от всех ее характеристик невозможно (обычно в подобных случаях стараются исключить из модели некоторые «несущественные» характеристики, что приводит к потере информации, которой и так недостаточно).

Тем не менее в рассмотренных нами примерах его применения игнорируется одно важное обстоятельство.

Выше мы привели зависимость стоимости листогибочных кривошипных прессов от номинального усилия пресса и длины рабочего стола из работы [4]. Степенной характер этой зависимости не случаен – как правило, стоимость машин связана с ее техническими характеристиками именно степенно ́ й зависимостью. Да и оценщики нередко связывают стоимость машины с ее «основной характеристикой» (производительностью, мощностью и т. п.) именно степенно ́ й зависимостью, именуя соответствующий показатель степени коэффициентом торможения или коэффициентом Чилтона (см. [3, 6]).

Между тем в методе направленных корректировок различия в значениях отдельных характеристик учитывались путем аддитивной добавки (такое же допущение нередко принимается, когда для оценки объекта используется регрессионная модель). Точно так же, оценивая тесноту связей между стоимостью и отдельными характеристиками, мы имели в виду, что наиболее тесной является линейная, а не степенна ́ я зависимость.

Однако степенна ́ я зависимость превращается в линейную, если заменить характеристики машин их логарифмами. Тогда уже описанная «линейная» версия метода главного фактора превращается в «логарифмическую». При этом таблица с исходной информацией о характеристиках и стоимостях машин становится вспомогательной, а в основной расчетной таблице помещаются логарифмы этих величин. Результаты подобного расчета применительно к примеру 2 представлены в таблице 4.

Результаты оценки стоимости машины методом главного фактора (логарифмическая версия)

Таблица 4

Характеристика	Машина							Коэффициент детерминации
	М0	М1	М2	М3	М4	М5	М6
F	0,667	1,307	0,989	0,304	-0,741	-1,127	-1,399
ln X 1	-0,9163	-1,6094	-1,2040	-0,6931	0,2311	0,6366	0,9243	0,9968
ln X 2	-0,0943	-0,0943	-0,0943	-0,0943	-0,0834	-0,0834	-0,0834	0,8895
ln X 3	2,4849	1,7918	2,1972	2,7081	3,6243	4,0342	4,3255	0,9967
ln X 4	1,0986	-0,6931	0,0000	1,0986	1,6094	2,1972	2,4849	0,8927
ln X 5	0,7885	0,7885	0,7885	1,1632	1,4351	1,4351	1,4351	0,9066
ln X 6	3,8712	3,1781	3,5835	4,1109	5,0239	5,4293	5,7170	0,9971
ln X 7	1,6487	1,3863	1,5041	1,8563	2,7081	3,1135	3,4012	0,9833
ln V	7 , 3210	6,9499	7,1293	7,6430	7,9963	8,3129	8,5949	0,9828
V = 1 511 , 6								7 , 6455

Как видим, на этот раз результаты расчета по разным версиям метода существенно различаются. Однако значение V = 1 511 , 6 предпочтительнее по трем причинам:

• 1)    зависимости стоимости машин от их характеристик обычно нелинейные;

• 2)    коэффициент детерминации между главным фактором и стоимостью машин в таблице 3 намного ниже, чем в таблице 4;

• 3)    как видно из таблиц 3 и 4, машина М0 по всем характеристикам является средней между машинами М2 и М3. Но тогда и ее стоимость ( V ) должна лежать в пределах между стоимостями машин М2 и М3, то есть от 1 248 до 2 086, как и получилось в таблице 4. В тех же пределах лежит и стоимость машины М0, оцененная методом направленных корректировок – она будет равна полусумме стоимостей М2 и М3, то есть (1 248 + 2 086) / 2 = 1 667. Однако расчет по линейной версии метода главного фактора (табл. 3) дает оценку V = 2 336 , 5, выходящую за указанные пределы.

При применении методов главного фактора и направленных корректировок предполагается, что зависимости стоимости машин от их характеристик точно не известны. По этой причине говорить о точности этих методов затруднительно. Однако ее можно оценить косвенно, применив тот или иной метод к оценке какой-либо машины в параметрическом ряду, стоимость которой известна. Представляется, что оценки методом главного фактора окажутся более точными.

В заключение отметим, что предложенный метод допускает обобщения, по крайней мере, в четырех направлениях.

Во-первых, выделив один главный фактор, затем можно выделить и второй, и третий, и т. д., что позволит полнее использовать имеющуюся у оценщика информацию об оцениваемой машине и ее аналогах. Процедура такого выделения и одновременного нахождения стоимости оцениваемой машины становится сложнее (для метода главных компонент эта процедура описана в работах [6–9]). Однако, когда аналогов не очень много, а различные их характеристики достаточно тесно связаны, обобщенный в этом направлении метод не сильно изменит получаемые результаты.

Во-вторых, этот метод удобен для того, чтобы одновременно оценивать несколько машин по данным об одних и тех же аналогов. Пусть, скажем, в условиях примера 2 надо оценить не только машину М0, но и машину М5. В этом случае аналогами будут выступать машины М1, М2, М3, М4 и М6. Порядок расчетов при этом не изменится, но результаты окажутся иными: оценки стоимостей машин М0 и М5 составят соответственно 1 518 и 4 401. Полученная стоимость машины М5 отклоняется от известной (4 076) на 7 процентов, что не так уж много, учитывая не слишком большой объем исходной информации. Кстати, если бы здесь требовалось оценить машину М2, то отклонение было бы меньше.

В-третьих, как и в методе направленных корректировок, здесь можно учесть важность, «весомость», отдельных характеристик машины. Для этого при суммировании коэффициентов детерминации отдельным слагаемым можно придавать те или иные веса. Правда, это, как отмечено в работе [2], внесет в результаты расчетов «некоторый субъективизм».

Наконец, в-четвертых, предложенный метод хорошо «комбинируется» с другими методами оценки, основанными на использовании регрессионных зависимостей. Покажем это на примере линейной версии метода.

Пусть, например, на основе какой-то (имеющейся или дополнительной) информации установлена регрессионная зависимость стоимости машин от одной из их характеристик (скажем, мощности) X1 : V ≈ a + bX1 (поскольку зависимость здесь регрессионная, а не точная, мы используем знак приближенного равенства). Отклонения стоимостей аналогов от рассчитанных по такой зависимости обычно объясняют влиянием «случайных», неучтен- ных, факторов. Однако в данном случае их можно объяснить и влиянием других учитываемых факторов. Это делается следующим способом.

Построим (используя только имеющуюся информацию о характеристиках машин) регрессионные зависимости каждой характеристики от X1: X2 ≈ a2 + b2X1, X3 ≈ a3 + b3X1,  Затем для каждой машины рассчитаем разности: Y2 = X2 – a2 – b2X1, Y3 = X3 – a3 – b3X1, ..., а для каждого аналога – еще и разности d = V – a – bX1, то есть отклонения стоимостей от рассчитанных по регрессионной модели. После этого применим метод главного фактора (в линейной версии), взяв в качестве характеристик машин величины Y2, Y3,.. , а в качестве их стоимостей – поправки к стоимостям, то есть величины d. Проведя расчеты, аналогичные представленным на рисунке или в таблице 3, мы получим поправку d к стоимости оцениваемой машины, после чего саму эту стоимость можно будет оценить суммой V = a + bX1 + d.

Представляется, что с учетом изложенного использование метода главного фактора позволит повысить обоснованность расчетов рыночной стоимости машин и оборудования.