Метод матричных пучков для оценки параметров векторных процессов

Автор: Генри Манус Патрик, Ибряева Ольга Леонидовна, Салов Данил Дмитриевич, Семенов Александр Сергеевич

Журнал: Вестник Южно-Уральского государственного университета. Серия: Математическое моделирование и программирование @vestnik-susu-mmp

Рубрика: Программирование

Статья в выпуске: 4 т.10, 2017 года.

Бесплатный доступ

В работе рассматривается один из современных параметрических методов обработки сигналов - метод матричных пучков (ММП). Метод позволяет по отсчетам сигнала, представляющего собой сумму комплексных экспонент, эффективно оценивать его параметры. Число экспонент не предполагается известным заранее и также может быть оценено с помощью сингулярного разложения матрицы, составленной из отсчетов сигнала. Объектом исследования данной работы служит векторный процесс - набор сигналов, имеющих одинаковые частоты и коэффициенты затухания (т.е. одинаковые полюсы сигнала), но, вообще говоря, различные комплексные амплитуды. Сигналы такого вида возникают, например, при рассмотрении фазированной антенной решетки, когда необходимо оценить параметры сигнала, генерируемого одними и теми же источниками, но приходящими от многих антенных элементов со своими амплитудами и фазами. Подобная задача возникает и при оценке параметров сигналов с двух пространственно-распределенных датчиков движения кориолисового расходомера. При обработке набора сигналов классическим ММП мы получаем наборы различных полюсов этих сигналов, которые далее приходится, например, усреднять, чтобы получить искомые значения полюсов, предполагаемых одинаковыми для этих сигналов. Предложенная в работе модификация ММП работает со всеми сигналами сразу, давая один набор полюсов сигнала, и при этом оказывается эффективнее и по быстродействию, и по точности определения параметров сигналов. В работе приведены алгоритмы классического ММП и его модификации для векторного процесса, а также численные эксперименты с модельными и реальными сигналами, снятыми с одного из серийно выпускаемых кориолисовых расходомеров Ду15. Эксперименты показывают, что предложенный алгоритм дает более точные результаты за меньшее (примерно в 1,5 раза) время, нежели классический метод матричных пучков.

Еще

Метод матричных пучков, параметрические методы оценки сигналов, сумма комплексных экспонент, сингулярное разложение, векторные процессы

Короткий адрес: https://sciup.org/147159462

IDR: 147159462 | DOI: 10.14529/mmp170409

Текст научной статьи Метод матричных пучков для оценки параметров векторных процессов

Преобразование Фурье является одним из самых изученных, универсальных и эффективных методов исследования сигналов [1, 2]. Это определяет его непрерывное совершенствование и появление методов, тесно связанных с ним, но превосходящих по некоторым характеристикам. Например, используя преобразование Гильберта [3], легко реализовать амплитудную и фазовую демодуляцию несущей, a. PRISM [4] позволяет эффективно работать со случайными сигналами, представленными суммой затухающих комплексных экспонент. Тем не менее, эти преобразования можно отнести к непараметрическим методам [1], имеющим принципиальное ограничение на разрешение частот, связанное со временем наблюдения соотношением неопределенности: Аш ~ ^Т, где Аш и AT - необходимое разрешение по частоте и время наблюдения, необходимое для его обеспечения, соответственно. Это соотношение накладывает жесткие требования на длительность наблюдаемого участка при требованиях повышенного разрешения, что, в свою очередь, ухудшает динамические характеристики алгоритмов обработки и затрудняет работу с нестационарными сигналами. Преобразование Гильберта - Хуанга [5] расширяет возможность работы с нестационарными нелинейными сигналами, однако к настоящему времени оно основано больше на эмпирических выводах, что затрудняет выработку рекомендаций по его конкретному применению.

Одним из способов преодолеть соотношение неопределенности является переход к параметрическим методам обработки сигналов, в которых предполагается, что сигнал состоит из суммы парциальных сигналов известной формы (обычно ортогональных по времени или частоте), а неизвестны только некоторые параметры сигнала. Например, если в качестве парциального сигнала используется комплексная синусоида, то параметрами являются комплексная амплитуда и частота каждой компоненты. Исходя из принципов решения систем независимых уравнений, это дает возможность снизить число отсчетов сигнала до числа неизвестных параметров, что может быть на порядки меньше числа отсчетов, необходимых для использования в преобразовании Фурье с теми же характеристиками по разрешению. Пожалуй, самыми известными методами этого класса являются алгоритмы, основанные на регрессионных процессах и процессах скользящего среднего [1]. Тем не менее, если сигнал можно представить в виде линейной комбинации экспоненциальных функций y ( t ) = ^ M =1 R _m e ⁽ ^a m + ^iUm ) ^t, достаточно широко используется метод Пропп, предложенный еще в конце 18 века [6]. Основной недостаток этого метода - необходимость точного знания числа экспоненциальных компонент, входящих в сигнал, и достаточно сильная чувствительность к аддитивным шумам [7]. Стремление преодолеть эти недостатки привели к появлению одного их самых эффективных методов спектрального анализа - метода матричных пучков (ММП) [8]. При этом число экспоненциальных компонент M определяется в ходе работы метода. Кроме того, как показывают исследования, ММП обладает существенно большей устойчивость к аддитивным шумам, чем метод Прони, и приближается по этому параметру к оценке Рао - Крамера [9].

В классической постановке метод предполагает использование SVD разложения матрицы, полученной из отсчетов сигнала для оценки всех параметров (амплитуды, частоты, фазы, затухания) парциальных экспонент. Это означает, что, в соответствии с классификацией алгоритмов по числу входов и выходов [10], он относится к классу SIMO (Single In, Multiple Out). Несмотря на широкое распространение систем такого вида, все больший интерес, связанный, прежде всего, с развитием теории обработки пространственно-временных сигналов, вызывают системы MIMO (Multiple In, Multiple Out). Типичным представителем систем такого вида является фазированная антенная решетка, в которой необходимо оценить параметры сигнала, генерируемого одними и теми же источниками, но приходящими от многих антенных элементов со своими амплитудами и фазами [11].

Еще одним примером подобного рода является кориолисов расходомер, в котором необходимо обрабатывать сигналы, приходящие от двух пространственно разнесенных датчиков. Использование классического метода для сигналов подобного типа предполагает раздельную обработку сигналов с каждого выхода. Однако при этом в каждом канале обработки, в общем случае, могут быть получены собственные оценки параметров, не совпадающие с остальными. Поэтому возникает проблема дальней- шей обработки оценок параметров. В случае близких значений параметров компонент эта проблема усугубляется необходимостью решения задачи группировки параметров идентичных компонент, то есть выделения в каналах оценок, принадлежащих одной и той же моде.

Таким образом, встает задача модификации ММП, с сохранением его преимуществ, применительно к задаче оценки параметров векторных сигналов. Этой проблеме посвящена настоящая статья. Под векторным сигналом (процессом) мы понимаем набор из K сигналов у i( t ) ,у 2( t ) ,...,ук ( t ). г.те yk ( t ) = ^ M =₁ Rmke ⁽ ^a m ⁺ i^ m ) t, k = 1 ,... ,K, имеющих одинаковые частоты ш ₁ ,ш ₂ ,...,ш _м и коэффициенты затухания а ₁ , а ₂ ,..., а _м (т.е. одинаковые полюсы сигнала), но, вообще говоря, различные комплексные амплитуды R ₁ _k , R ₂ _k ,..., R _Mk, k = 1 ,..., K.

Структура работы такова. В первой главе содержится описание классического алгоритма ММП. Его модификация на случай векторного сигнала приведена во второй главе. Так как аналитическое исследование предложенного алгоритма представляется затруднительным, далее в работе приведены результаты моделирования классического и модифицированного методов на модельном и реальном сигналах, показывающие эффективность предложенного метода. В заключении работы указаны возможные направления будущих исследований.

1. Классический метод матричных пучков

Метод матричных пучков используется для оценки параметров сигнала:

y ( t ) = Rke ^ a k + i^ k ) t

k =1

по его N отсчетам:

у (n ) = у (nT ) = £ Rke ⁽ ^a k ⁺ i- k ) ^nT = ^ Rk Zk. k =1 k =1

Здесь T - период дискретизации, R _k = A _kе^г ^фк - комплексныe амплитуды, a _k - коэф-
фициенты затухания, w _k = 2 nf _k - частоты и z _k - полюсы сигнала		у ⁽ t ) .
На первом шаге ММП находит полюсы z_k с помощью решения задачи на обоб-
щенные собственные значения пучка матриц, составленных из отсчетов сигнала у ( n ) .
Далее по найденным полюсам ММП находит оценки для R _k . Изложим подробнее алгоритм ММП.
Определим две матрицы Ya, Yb размеров ( N — L ) х L следующим образом:
Ya =	/ у ⁽ L ^— 1) ... у ⁽¹⁾ у ⁽⁰⁾ \ у ⁽ L ) ... у ⁽²⁾ у ⁽¹⁾	,
	• • • • • I I • • • • • у ⁽ N ^— ²⁾ ... у ⁽ N ^— L ) у ⁽ N ^— L ^— 1) ) / у ⁽ L ) ... у ⁽²⁾ у ⁽¹⁾ \ у ( L + 1) ... у (3) у (2)
Yb =	• • • • • I I • • • I • ^ ^у ⁽ N ^— 1) ... ^у ⁽ N ^— L + 1) ^у ⁽ N ^— L ) у	. (4)

Здесь M < L < N — M - параметр метода. Покавано [8]. что при выборе N < L < NN дисперсия оценки полюсов zk будет минимальна, т.е. ММП будет наименее чувствителен к шуму. В этой работе мы положили L = floor (N3) . (Функция floor в Matlab округляет до ближайшего целого.)

Для матриц Y„Yb справедлива следующая факторизация [8]:

Ya = ZlRZr, Yb = ZlRZZr. (5)

Здесь

Zl =

z 1

1 .

z 2 .

.. 1

. . zM

•

5 ZR =

_z ₁ L- 1 _z ₂ L- 1

L- 2 z ₁ . .

. 1

•

L-z ₂

N -L- 1 z ₁

N-L- 1 z ₂ .

•

N-L-. . z _M

”¹ 7

L- 1 z _M

L-z _M

•

. 1

R = diag ( R 1 , R ₂ ,..., RM ) , Z = diag ( z 1 , z ₂ ,..., z _M ) . (6)

Рассмотрим пучок матриц Y _b — XY _a = ZLR ( Z — XE ) Zr , где E - единичная матрица M -го порядка. Можно показать [8], что при M < L < N — M и X = zk, к = 1 ,..., M, ранг матрицы Y _b — XYa равен M. Однако, если X = zk, то k -ая строка матрицы Z — XE нулевая и ранг этой матрицы равен M — 1 .

Таким образом, полюсы zk = e ⁽ ^a k + ^k ) ^T могут быть найдены как обобщенные собственные значения пучка матриц Y _b — XY _a, т.е. как собственные значения матрицы Y^Yb. Здесь индекс f используется для обозначения псевдообратной матрицы.

В случае зашумленных данных матрицу Y _a для эффективной фильтрации шума необходимо подвергнуть операции сингулярного (SVD) разложения

Ya = USV^T.

Здесь U, V - унитарные матрицы, S - диагональная матрица, элементами которой являются сингулярные числа матрицы Y _a . (Верхний индекс Т означает операцию транспонирования.)

Заметим, что в случае отсутствия шума диагональная матрица S имеет ровно M ненулевых сингулярных чисел, все последующие равны нулю. В случае зашумленного сигнала ненулевых сингулярных чисел уже не будет, однако между первыми M и последующими сингулярными числами матрицы S будет наблюдаться ярко выраженный скачок, который и позволит определить число комплексных экспонент в сигнале.

Итак, сингулярное разложение матрицы Y _a позволяет определить число истинных экспонент сигнала M. Кроме того, оно может быть использовано для нахождения псевдообратной матрицы Y^. На практике используется усеченная до ранга M псевдообратная матрица:

M ₁

Ya = ^ vmum = V0S- 1UT5 (8) m=1 σm где ст 1, ...,стм - ’ это M наибольших сингулярных чисел матрицы Ya, vm 11 um -соответствующие им сингулярные векторы, V0 = (v о, ...,vM), U0 = (u 0, ...,uM), S0 = diag (ст 1,..., стм).

После нахождения матрицы У^ для оценки полюсов zk, к = 1 ,...,M, сигнала остается только найти M собственных чисел матрицы У^У_ь, или, в силу следующей

цепочки равенств: У У qk = zk qk, V) S-1UT Уь qk = zk qk, (9) S-1UTYbV) (VTqk) = zk (VTqk), найти M собственных чисел матрицы

Ze = S- ¹ UTYbV ) .

(Ю)

Далее в методе матричных пучков по известным M и zk находятся комплексные амплитуды Rk из решения следующей задачи:

y (0)

/ 1 1 .

.. 1

R 1

y (1) •

₌

z 1 z 2 .

• • .

. . zM

R 2

•

\ y ⁽ N ^-

1) /

• I

• •

( z NN^- ¹ zN^- ¹ .

•

• 1

N - ¹

. . z _M

•

R _M

(П)

Подведем итог описания классического ММП [8] в следующем виде:

Алгоритм 1. Классический метод матричных пучков

Вход: Отсчеты сигнала

MM y (n) = ^ Rke('+iyk) t = ^ Rkzn, n = 0, 1 ,...,N - 1.

k =1 k =1

Выход: Параметры сигнала Rk,z _k ,k = 1 ,... ,M.

1. Формируем матрицы У _а ,У _ь (3), (4).
2. Находим SVD-разложение матрицы У _а .
3. Оцениваем число M полюсов сигнала.
4. Находим усеченную до ранга M псевдообратную матрицу У^ (8).
5. Оцениваем z _k , вычисляя собственные значения матрицы ZE (10).
6. Оцениваем Rk, решая задачу (11) методом наименьших квадратов.
2. Метод матричных пучков для векторных процессов

Конец

Заметим, что данный алгоритм был уже многократно модифицирован под различные задачи. Например, в [12] предложен вариант ММП для незатухающих синусоид, улучшение ММП с помощью сохранения ганкелевой структуры матрицы, собственные числа которой дают полюсы сигнала, предложено в [13], версия ММП для квантовых компьютеров разработана в [14], в [15] предложен рекурсивный ММП и т.д.

Пусть у нас имеется K сигналов y 1( t ) ,y ₂( t ) ,... ,y _K ( t ) , имеющих одинаковые полюсы z 1 , z ₂ ,..., z _M , но, вообще говоря, различные комплексные амплитуды R i k,R 2 k,...,Кмь к = 1 ,...,K.

Запишем матрицы Yak,Y _bk, соответствующие сигналам yk ( t ) , k = 1 ,... ,K.

	^ yk ( L ^— 1)	... yk (1)	yk ⁽⁰⁾
	yk ( L )	... yk (2)	yk ⁽¹⁾
Yak =	• •	• • 1 •		, (12)
	• yk ( N — 2)	. . . ^yk ⁽ N ^— L )	* yk ⁽ N ^— L ^— 1)	/
	/ yk ( L )	... yk (2)	yk ⁽¹⁾	\
	yk ( L + 1)	... yk (3)	yk (2)
Ybk =	• •	• • 1 • 1		. (13)
	• yk ( N — 1)	. . . ^yk ⁽ N ^— L + 1) ^yk ⁽ N ^— L )
Напомним, что каждая из этих		матриц допускает факторизацию:

Yak = ZlR ⁽ ^k ) Zr, Ybk = ZlR ⁽ ^k ) ZZr. (14)

Здесь ZL, Zr, Z - те же матрицы, что и в (6), а матрица R ⁽ ^k ) определяется:

R ⁽ ^k ) = diag ( R 1 _к ,R 2 k ,...М ) . (15)

Из матриц Yak, Ybk составим бло^тшые матрицы YaE,Y _b E размеров ( N — L ) x LK следующим образом:

YaE ⁼

( Ya ¹

Ya 2

YaK

YbE ⁼

Yb 1

Yb 2

•

YbK

Легко видеть, что полюсы z _k являются обобщенными собственными значениями пучка матриц YbE — XYaE. Действительно, справедливо следующее разложение данных матриц:

YaE =

/ Ya 1 \ / ZlR ⁽¹⁾ Zr \

Ya 2 ZlR ⁽²⁾ Zr

YaK

YbE =

\ ZlR ⁽ ^K ) Zr / Yb 1 \ / Zl

Yb 2 0

I•

YbK0

« «

/ Zl0

••

••

••

... 0 \

... 0

«•

♦•

••

. . . ZL

... 0

«•

♦•

••

. . . ZL

/ R ⁽¹⁾ \

R ⁽²⁾

•

\ R ⁽ K ) )

/ R ⁽¹⁾ \ R ⁽²⁾

•

_R ( K )

ZZR.

Тогда, YbE — XYaE =

0 •

« «

понижающими ранг этой матрицы.

_R (1) R ⁽²⁾

_R ( K )

( Z — XE ) Zr 11 41 ката zk являются

Тогда, аналогично ММП для скалярного процесса, полюсы zk могут быть найдены как M собственных чисел матрицы YEY _bE , где YE = ^ M =1 Е v _m um = V Q S- ¹ U Q T - усеченная до ранга M псевдообратная матрица к Y _aE и число M определяется на основе скачка в сингулярных числах матрицы Y _aE.

Аналогично, как в предыдущем параграфе, получаем, что zk могут быть найдены как M собственных чисел матрицы:

ZE = S 0 ^- ¹ U 0 ^TYbEV 0 .

решения K задач:

Комплексные амплитуды Rmk находятся затем из yk(0) yk(1)

• yk(N - 1)

/ 1 1. .. 1 \ / R1k z1 « z2 . • 1 . . zM R2k « I z1N-1 1 N-1 z2 . • • 1 N-1 . . zM « « RMk / k= 1,...,K.

Подведем итог в виде следующего алгоритма:

Алгоритм 2. Метод матричных пучков для векторных процессов

Вход: Отсчеты K сигналов

Ук ( n ) = ^ Rmke ⁽ ' + i ^) t = ^ Rmkzm, k = 1 ,...,K,n = 0 , 1 ,...,N - 1 . k =1 k =1

Выход: Параметры сигналов R _mk , z _m ,m = 1 ,..., M, k = 1 ,..., K.

1. Формируем матрицы Y _aE ,Y _bE (12), (13).
2. Находим SVD-разложение матрицы Y _aE .
3. Оцениваем число M полюсов сигнала.
4. Находим усеченную до ранга M псевдообратную матрицу YE-
5. Оцениваем zk, вычисляя собственные значения матрицы Z _E (18).
6. Оцениваем R _mk , решая задачи (19) методом наименьших квадратов.
3. Моделирование работы алгоритмов

Конец

Далее с помощью численных экспериментов мы покажем, что нахождение полюсов z 1 , z 2 ,..., z _M , как обобщенных собственных значений пучка матриц YbE — XY _aE эффективнее (и по времени, и по точности определения), чем нахождение классическим ММП обобщенных собственных значений пучков Ybk — XY _ak, k = 1 ,..., K, с их последующим усреднением.

В этом параграфе рассмотрены результаты исследования двух алгоритмов при использовании модельного и реального сигналов.

Пример 1. Рассмотрим сигналы у 1 ,у 2 с одинаковы ми полюсами z 1 = 0 , 8070 + 0 , 5863 j, z 2 = 0 , 8484 + 0 , 5199 j и разными амплитудами и фазами:

у 1 = j e ¹⁰ t sin (2 п ■ 400 1 + 45) + 3 e ²⁰ t sin (2 п ■ 350 1 + 9Q) , у 2 = e- ¹⁰ t sin (2 п ■ 400 1 + ⁿ ) + 4 e^- ²⁰ t sin (2 п ■ 350 1 — 4 ^ ) .

Были обработаны 30 отсчетов сигналов у 1 и у2, полученные с частотой дискретизации Fs=4000 Гц. В качестве аддитивного шума были взяты значения нормальной случайной величины с нулевым мат. ожиданием и ст = 0, 005. Были рассмотрены двадцать зашумленных реализаций данных сигналов.

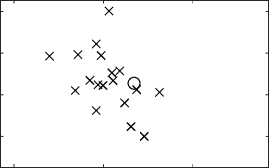
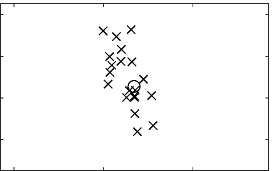
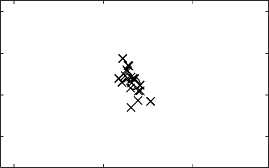
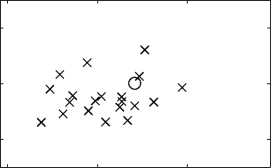
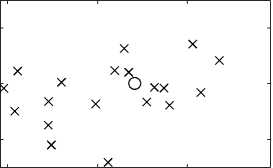
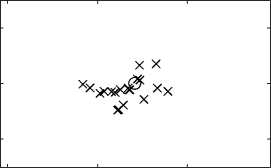
При помощи двух изложенных методов, были оценены полюсы z 1 , z 2 . На рис. 1 показано истинное значение полюсов сигналов и оценки параметров каждого из сигналов у 1 и у 2 , полученные классическим и модифицированным ММП, который обрабатывает два сигнала одновременно. Как можно видеть оценки для полюсов в первом случае имеют больший разброс относительно истинных значений полюсов, чем во втором.

0.595

0.59

0.585

0.58

0.78 0.8 0.82

Действительная

0.595

0.59

0.585

0.58

0.78 0.8 0.82

Действительная

0.595

0.59

0.585

0.58

0.78 0.8 0.82

Действительная

0.54

(X со

0.52

0.5

0.82 0.84 0.86

Действительная

0.54

сх со

0.52

0.5

0.82 0.84 0.86

Действительная

0.54

сх со

0.52

0.5

0.82 0.84 0.86

Действительная

Рис. 1. Оценки и истинное значения полюсов сигнала при помощи классического и модифицированного метода матричных пучков (реальное значение полюсов z 1 = 0 , 8070 + 0 , 5863 j и z 2 = 0 , 8484 + 0 , 5199 j отмечено кружком, а оцененное - крестиком)

Среднее значение получившихся (по 20 реализациям) полюсов сигнала £1, £2, их разница с истинными значениями z 1 , z2, среднеквадратичное отклонение (СКО), а также время работы приведены в таблице.

Таблица

Сравнение методов

	ММП, для у 1	ММП, для у 2	Векторный ММП
Ср. значение Z 1	0,8066 + 0,5864 i	0,8062 + 0,5876 i	0,8069 + 0,5866 i
CKO z i	0,0050	0,0042	0,0017
Разница z 1 — z 1	4,43е-04 — 5,80e-05 i	0,0008 — 0,0013 i	6,88е-05 — 2,46e-04 i
Ср. значение z ₂	0,8473 + 0,5199 i	0,8420 + 0,5192 i	0,8479 + 0,5197 i
CKO z 2	0,0076	0,0169	0,0037
Разница z 2 — z ₂	0,0011 — 0,0 001 i	0,0064 + 0,0007 i	5,04e-04 2,14e-04 i
Время работы, с	0,0571		0,0418

Как можно видеть, модифицированный метод матричных пучков, используя совместную оценку двух сигналов, дает более точную оценку полюсов, а также выигрывает по быстродействию.

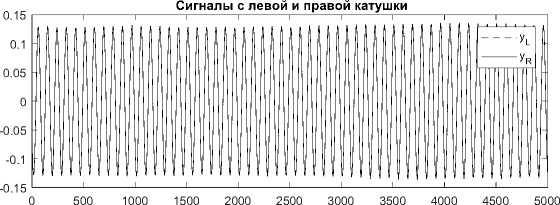
Пример 2. Далее рассмотрим сигналы, полученные с двух пространственно разнесенных датчиков движения измерительных трубок кориолисового расходомера. В соответствии с принципами работы кориолисова расходомера, сигналы должны иметь одинаковую частоту, но разные фазы (при наличии потока измеряемой жидкости) и амплитуды (в силу не возможности абсолютной идентичности правой и левой частей расходомера). Сигналы представлены на рис. 2.

0.15

0.1

-0.15

Сигналы с левой и правой катушки (вблизи)

0.05

-0.05

-0.1

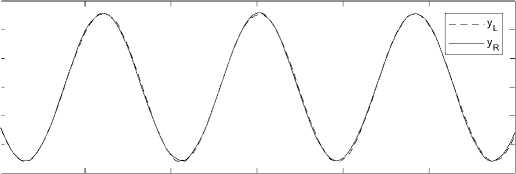
Рис. 2. Сигналы с кориолисового расходомера

Данные реальные сигналы были обработаны с окном в N = 100 и частотой дискретизации Fs = 8192 Гц при помощи классического и модифицированного метода матричных пучков. Для частоты сигналов было получено значение 90,3 Гц с СКО, равным 0,25 для классического и 0,11 для модифицированного ММП. Разность фаз составила 0,015 с СКО, равным 0,0164 и 0,0029 соответственно.

На рис. 3 приведены значения амплитуды сигналов расходомера с левой и правой катушек. Как можно видеть, модифицированный ММП дает существенно меньшую дисперсию и в оценке этого параметра.

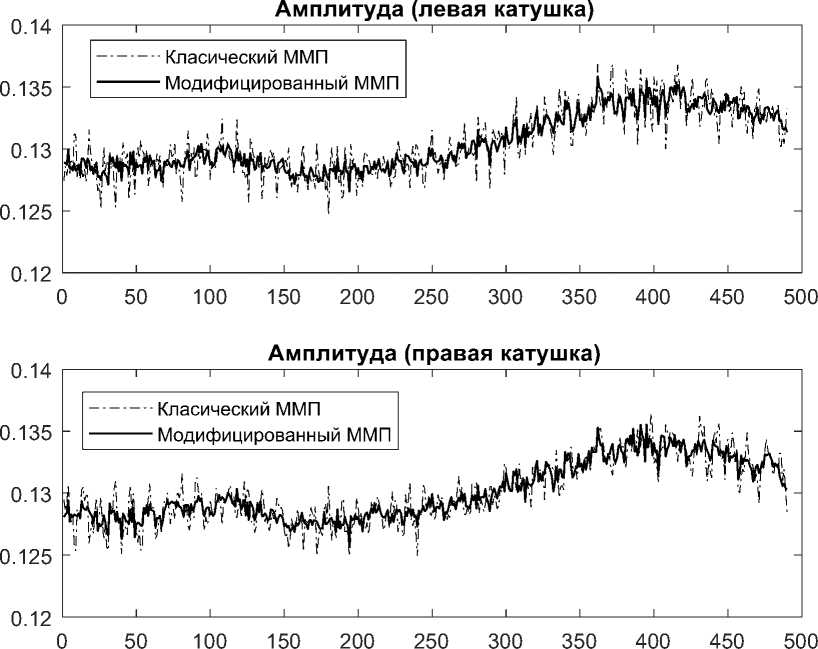
Рис. 3. Значения амплитуды сигналов с правой и левой катушек

Итак, при определении всех параметров (частота, амплитуды, разность фаз) дисперсия оценки данного параметра в случае применения модифицированного ММП меньше, чем для классического. Кроме того, модифицированный ММП при нахождении данных параметров выигрывает и по быстродействию (примерно в 1,5 раза быстрее, чем классический ММП).

Заключение

В данной работе предложена модификация метода матричных пучков для векторных процессов. Результатами моделирования работы алгоритмов подтверждено, что модифицированный ММП быстрее и точнее находит параметры векторного процесса, чем классический ММП. Дальнейшие исследования предполагают разработку рекуррентного ММП для векторных процессов, т.е. на обобщение статьи [15].

Работа проводилась при финансовой поддерэюке Министерства образования и науки Российской Федерации прикладных научных исследований ^Разработка отечественного массового кориолисового расходомера для нефтегазовой промышленности с функцией измерения расхода многофазных потоков». Соглашение № 14.578.21.0191 от 03 октября 2016 года. Уникальный идентификатор прикладных научных исследований RFMEFI57816X0191.

Список литературы Метод матричных пучков для оценки параметров векторных процессов

Marple, S.L. Digital Spectral Analysis: with Applications/S.L. Marple. -Upper Saddle River: Prentice-Hall, 1987.
Сергиенко, А.Б. Цифровая обработка сигналов/А.Б. Сергиенко. -СПб.: Питер, 2002.
Rabiner, L.R. Theory and Application of Digital Signal Processing/L.R. Rabiner, B. Gold. -Upper Saddle River: Prentice-Hall, 1975.
Henry, M.P. Prism Signal Processing for Sensor Condition Monitoring/M.P. Henry, O. Bushuev, O. Ibryaeva//2017 IEEE 26th International Symposium on Industrial Electronics ISIE 2017 (Edinburgh, UK, 19-21 June 2017). -2017. -P. 1404-1411.
Huang, N.E. A Review on Hilbert -Huang Transform: Method and Its Applications to Geophysical Studies/N.E. Huang, Z. Wu//Reviews of Geophysics. -2008. -V. 46, № 2. -P. 1-23.
Prony, G. Essai experimental et analytique: sur les lois de la dilatabilite de fluides elastiques et sur celles de la force expansive de la vapeur de l'еau et de la vapeur de l'alkool, a differentes temperatures/G. Prony//Journal de l'Ecole polytechnique floreal et plairia. -1795. -V. 1, № 2. -P. 24-76.
Kumaresan, R. A Prony Method for Noisy Data: Choosing the Signal Components and Selecting the Order in Exponential Signal Models/R. Kumaresan, D.W. Tufts, L.L. Scharf//Proceedings of the IEEE. -1984. -V. 72, № 2. -P. 230-233.
Hua, Y. Matrix Pencil Method for Estimating Parameters of Exponentially Damped/Undamped Sinusoids in Noise/Y. Hua, T.K. Sarkar//IEEE Transactions on Acoustics, Speech, and Signal Processing. -1990. -V. 38, № 5. -P. 814-824.
Sarrazin, F. Comparison Between Matrix Pencil and Prony Methods Applied on Noisy Antenna Responses/F. Sarrazin, A. Sharaiha, P. Pouliguen//Loughborough Antenna and Propagation Conference. -Лафборо, 2011. -P. 1-4.
Patton, R. Fault Diagnosis in Dynamic Systems: Theory and Application/R. Patton, P. Frank P, R. Clark. -Upper Saddle River: Prentice-Hall, 1989.
Воскресенский, Д.И. Активные фазированные антенные решетки/Д.И. Воскресенский, А.П. Канащенков. -М.: Радиотехника, 2004.
Enrique, J. Comparison between the Matrix Pencil Method and the Fourier Transform Technique for High-Resolution Spectral Estimation/J. Enrique, F. Rio, T.K. Sarkar//Digital Signal Processing. -1996. -V. 6. -P. 108-125.
Lu, B. Improved Matrix Pencil Methods/B. Lu, D. Wei, B.L. Evans//Asilomar Conference on Signals, Systems, and Computers. -1998. -V. 2. -P. 1433-1437.
Steffens, A. An Efficient Quantum Algorithm for Spectral Estimation/A. Steffens, P. Rebentrost, I. Marvian//New Journal of Physics. -2017. -V. 19. -Article ID 033005. -14 p.
Ibryaeva, O.L. Recursive Matrix Pencil Method/O.L. Ibryaeva//IEEE Explore, II International Conference on Measurements, Chelyabinsk, 16-19 October, 2017.

Еще

Статья научная