Метод парных продаж. Еще раз о границах применимости

* первоначально материал статьи был размещен на портале « вестник оценщика» (url: http:// ), опубликован (с сокращениями) в журнале «Оценочная деятельность» (2014. № 1/3. С. 83–86. URL: и в журнале «Регистр оценщиков» (2014. № 17. С. 17–22). URL: html

Авторам не удалось найти в доступных источниках конкретных рекомендаций 9 относительно числа пар цен, используемых в МПП. Более того, в широко распространенных источниках, указанных ранее, описывается как корректный расчет корректировок именно по одной паре цен. Тем не менее отметим, что авторы ряда других публикаций (см., например [5, 14–16]) предупреждают о ненадежности расчета поправок, полученных по одной паре продаж, либо ставят под сомнение практическую пригодность метода расчета по одной паре или демонстрируют расчет поправки как средней по нескольким парам цен.

Проверка метода на нескольких парах цен

Представляется интересным продолжить исследование точности расчета корректировки в рамках МПП для случаев усреднения ее по двум и трем парам цен. Методология оценки неопределенности (погрешности) поправки аналогична использованной в работе [1], к которой мы и отсылаем заинтересованного читателя.

Сфокусируемся на отличиях, в частности на числовом примере, вызвавшем много вопросов при обсуждении. Чтобы решить их, сформируем «модельный» пример, отвечающий типичной оценочной ситуации – расчет величины поправки к цене, отражающей небольшое отличие двух сравниваемых объектов. С помощью датчика случайных чисел в MS Excel сгенерируем две группы (А и В) по пятнадцать чисел из нормального распределения, задавая статистики распределения, близкие к наблюдаемым на рынке 10 (см. с. 8).

Каждое число в двух группах (по 15 чисел) принято за цену реального товара, отличающегося от второго каким-то одним свойством. Согласно общепринятым представлениям считается, что цены в группе А (с меньшим средним значением) соответствуют товару с худшим значением (или отсутствием) свойства, по которому различаются товары. Далее группы цен А и В считаются генеральными совокупностями (всеми ценами на каждый товар на рынке). При этом «истинной» считается поправка, полученная как разность средних цен по

	А		В
	а1	19 036	b1	18 913
	а2	20 648	b2	18 912
	а3	17 995	b3	21 184
	а4	17 254	b4	19 531
	а5	19 192	b5	22 395
	а6	17 825	b6	17 944
	а7	17 876	b7	19 605
	а8	17 152	b8	18 004
	а9	18 409	b9	21 022
	а10	21 325	b10	21 537
	а11	18 495	b11	18 870
	а12	16 006	b12	19 226
	а13	17 170	b13	18 899
	а14	17 591	b14	22 536
	а15	18 387	b15	20 115
Среднее значение	18 291		или	19 913
Минимальное значение	16 006			17 944
Максимальное значение	21 325			22 536
Стандартное отклонение	1 317			1 436
Коэффициент вариации, %	7			7
Коэффициент осцилляции, %	29			23
Количество элементов	15			15
«Истинная» поправка В ср – А ср	1 622			9% 11

группам ( В _ср – А _ср = 1 622). В дальнейших расчетах она будет служить базой для оценки погрешности (неопределенности) расчета остальных поправок.

На основе сгенерированных генеральных совокупностей цен рассчитаем все возможные поправки по одной, двум и трем парам цен. Ограничение числа усредняемых разностей пар цен на уровне трех прежде всего объясняется условиями рынка. Для большинства оцениваемых объектов на реальных рынках подбор большего числа

«согласованных пар» аналогов, различающихся лишь по одному свойству, представляется нереальной задачей. Кроме того, использование большего числа пар, скорее, могло быть названо методом статистической обработки, нежели методом парных продаж.

Поправка по одной паре цен

Всего в нашем примере имеется 15 х 15 = = 225 пар цен 12, поэтому может быть получено 225 поправок, рассчитанных по каж- дой паре. Часть из них будут отрицательными и, следовательно, восприниматься как лишенные экономического смысла 13. Отбрасывая такие значения, получим 184 положительных значения поправки и гистограммы, представленные на рисунках 1 и 2.

Минимальные и максимальные значения отношения «положительной» поправки, полученной по одной паре цен , к «истинной» составляют 0,006 и 4,03 соответственно.

Иными словами, в каждом отдельном расчете по одной паре цен относительная погрешность 14 оценки «истинной» поправки может составлять -99,4–303 процента.

Поправка по двум парам цен

Если поправку получать как среднее значение разности цен по двум парам, то всего в нашем примере может быть полу-

H 35

30 T

■ IIIIIH

CD i- CM Tt CO

UD О UD О ^ ^ CM

CM co

CM UD

CM

CM

CM UD

UD CM О

UD

CM UD

UD

CD CM О

CO

UD

CO

поправка (разность цен), р.

Рис. 1. Распределение поправки по одной паре цен 15

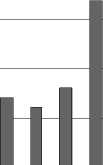
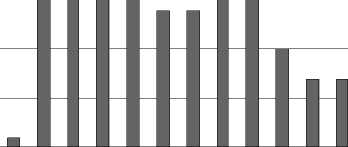
поправка /«истинная» поправка

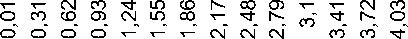
Рис. 2. Распределение отношения поправки по одной паре к истинной поправке

чено С2225 =25200 «двоек», где Сnm – число сочетаний из n по m. Мы помним, что экономически обоснованными считаются лишь положительные поправки (которых всего 184), поэтому рассматриваются лишь те «двойки», в которых обе пары дают положительные значения. Если хотя бы в одной из двух пар цен поправка отрицательная, то такая «двойка» игнорируется и на результат анализа не влияет 16. В результате такого отбора получим С1284 = 16836 положительных значений средней по двум парам поправки и гистограммы (см. рисунки 3 и 4).

” 400

о

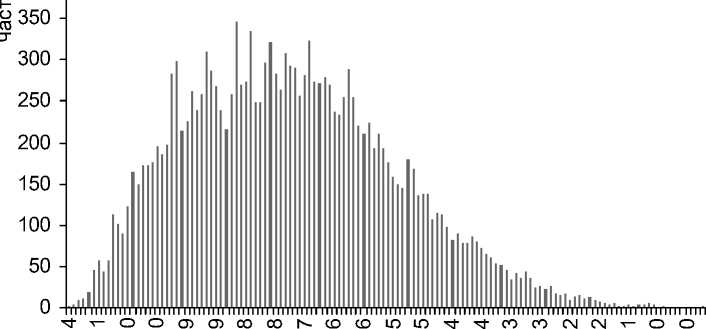
^COCDO)(NLOCO^^SOCOCDO)MIOCO^^SOCO

^^^(NCNCNCOCOCOCO^’xT'xr LO LO LO CD CD поправка (средняя разность цен), р.

Рис. 3. Распределение значений поправки по двум парам

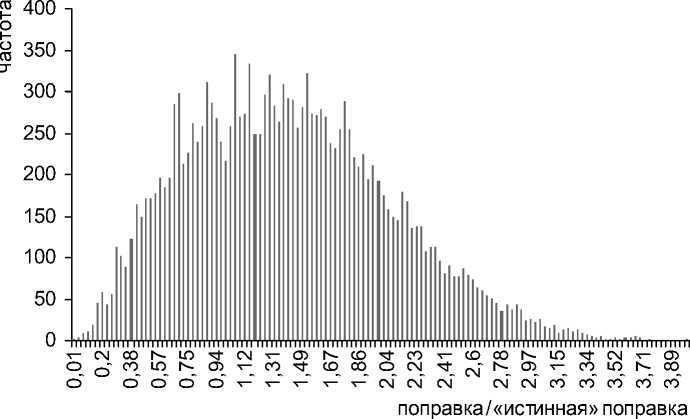
Рис. 4. Распределение отношения поправки по двум парам к истинной поправке

Минимальные и максимальные значения отношения средней поправки, полученной по двум парам цен, к «истинной» составляют 0,013 и 3,98 соответственно. По сравне- нию с поправками, полученными по одной паре цен, возможная погрешность расчета с точки зрения практики оценки не изменилась (-98,7–298% против -99,4–303%).

Поправка по трем парам цен

Для расчета средней по трем парам цен поправки число возможных «троек» в нашем примере будет С2325 = 1 873 200. Как и для случая двух пар, средняя по трем парам поправка вычисляется лишь тогда, ког- да вся «тройка» пар дает положительные значения поправок. То есть любая «тройка» пар хотя бы с одной отрицательной поправкой игнорируется 17. В результате получены С1384 = 1 021 384 тройки положительных поправок и гистограммы вычисленных средних значений (см. рисунки 5 и 6).

3 500

3 000

2 500

2 000

1 500

1 000

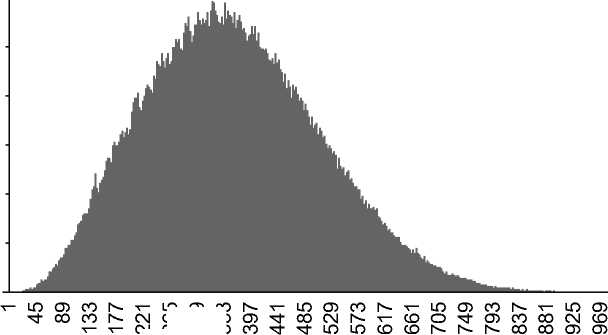
Ю CD СО (О О Ш CXI CXI СО СО поправка (средняя разность цен), р.

Рис. 5. Распределение значений поправки по трем парам

3 500

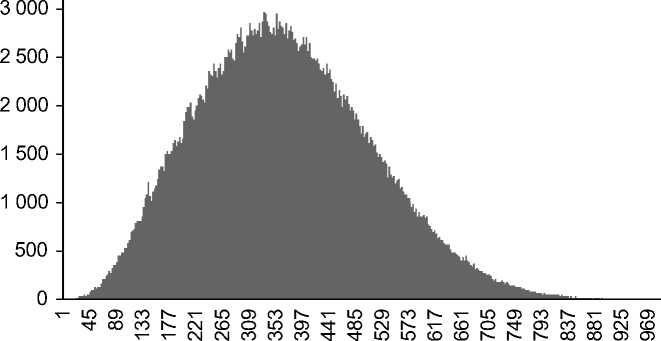
поправка/«истинная» поправка

Рис. 6. Распределение отношения поправки по трем парам к истинной поправке

Минимальные и максимальные значения отношения средней поправки, полученной по трем парам цен, к «истинной» составляют 0,023 и 3,79 соответственно. И в этом случае уменьшение возможной по- грешности расчета по сравнению с расчетом поправки по одной паре цен не имеет практического значения (-98–279% против -99–303%).

Эмпирические статистики распределе-

¹⁷ Результаты расчета по игнорируемым «двойкам» пар цен и отдельным их парам, дающим положительные поправки, рассмотрены ранее.

Параметр	Поправка
	по одной паре	по двум парам	по трем парам
Среднее	2 251	2 251	2 251
Стандартная ошибка	111	8	1
Медиана	1 913	2 180	2 200
Мода	Н/Д	123,4	Н/Д
Стандартное отклонение	1 510	1 062	865
Эксцесс	-0,50	-0,27	-0,19
Асимметричность	0,59	0,41	0,33
Интервал	6 521	6 438	6 113
Минимум	9	21	37
Максимум	6 530	6 460	6 150
Коэффициент осцилляции, %	290	286	272
Коэффициент вариации, %	67	47	38
Минимум/истинная поправка	0,006	0,013	0,023
Максимум/истинная поправка	4,03	3,98	3,79
Счет	184	16 836	1 021 384

ния значений поправок, рассчитанных по трем рассмотренным алгоритмам, представлены в таблице.

Погрешность на одном уровне

По сути, рассматривается задача об исследовании распределения средних (по двум и трем элементам) значений из конечной генеральной совокупности (см., например, [18]), в нашем случае состоящей из 184 элементов. Такой подход открывает путь к количественному анализу возможного разброса поправки в зависимости от доли отбора, то есть в нашем случае для отношения числа пар, по которым берется поправка, к общему числу доступных пар, дающих неотрицательные поправки.

Как видно из таблицы, увеличение объема обрабатываемых данных ожидаемо сказывается положительно на точности расчета поправок – снижаются интервалы их значений, а также коэффициенты вариации и в меньшей степени осцилляции.

Однако усреднение поправок по двум и даже трем парам цен существенно не меняет картину. Сужение интервала значений поправок с 6 521 (9–6 530) до 6 113 (37– 6 150) при «истинном» значении поправки 1 622 практического значения не имеет – неопределенность (погрешность) расчета неприемлемо велика во всех рассмотренных случаях.

В рассмотренном примере существенное отклонение рассчитанного по одной-трем «парным продажам» значения поправки от истинного прежде всего обусловлено тем, что интервалы распределения цен сравниваемых товаров пересекаются. В такой ситуации (а она является типичной на реальных рынках) увеличение числа парных продаж до трех не устраняет недопустимо большую погрешность (неопределенность) величины поправки.

Таким образом, основной вывод публикации [1] в отношении метода парных продаж остается в силе, по крайней мере для наиболее распространенной на практике ситуации. И этот вывод справедлив как для «неправильного» (по одной паре цен) при- менения метода, так и для «правильного» (по трем парам цен). В обеих ситуациях погрешность (неопределенность) расчета поправки сохраняется практически на исходном уровне (сотни процентов).

Существует ли какая-либо область корректного применения метода парных продаж?

Авторам настоящей статьи представляется, что там, где выполняется основанная предпосылка МПП – отсутствие или пренебрежимо малый разброс цен на товары «сравнимой пары», применение этого метод может давать адекватные результаты. Например, такое возможно при расчете поправки по отпускным ценам одного завода-изготовителя, или, в более общем случае для гомогенных товаров, по ценам «сравниваемой пары» у одного продавца. Другое дело, что подобные случаи не делают погоды в оценке.

МПП и рынок недвижимости

В заключение рассмотрим еще один аспект, в отношении которого у участников обсуждения возникли противоположные мнения. Речь идет о признании возможного разброса цен на один и тот же объект недвижимости. В пользу наличия такого разброса высказывается Макс Каммероу в своей публикации [20], а также Юджин Па-симовски в работах [21–22].

Авторы настоящей публикации разделяют эту точку зрения. Они исходят из того, что пока не сформулированы гипотезы и, следовательно, нет оснований полагать , что выявленное на рынке гомогенных товаров явление разброса цен на идентичные товары не могло бы быть распространено на другие сегменты рынка, включая рынок недвижимости.

Экспериментально подтвердить наличие такого, по выражению М. Каммероу, «виртуального» 18 разброса цен на недвижимость не так просто, и над этим еще предстоит поработать. Пока же можно сослаться на результаты локального опроса риелторов и оценщиков города Омска, проведенного в июне 2013 года 19, согласно которым разброс цен сделок при продаже квартир и объектов индивидуального жилищного строительства, не зависящий от характеристик недвижимости, может достигать 20–30 процентов. Эти результаты близки к мнению Ю. Пасимовски о наличии «внутреннего» разброса цен на недвижимость (до 30 процентов) вследствие того, что рынок недвижимости не является совершенным.

Конечно, необходимо проводить подобные опросы с привлечением большего числа участников, равно как и пытаться непосредственно выявлять разброс цен на «почти одинаковые» объекты недвижимости там, где это возможно. Однако уже имеющиеся данные позволяют сделать вывод о том, что метод парных продаж, широко описываемый в оценке недвижимости, не может претендовать на корректное использование в качестве количественного метода расчета корректировок.