Метод синтеза особого управления для автономных динамических систем

К настоящему времени существует достаточно разработанная общая теория оптимального управления, которая позволяет решить задачу «в принципе». Однако известно, что от общих воззрений до конкретного результата зачастую лежит достаточно большая дистанция, в том числе и в случае численного решения поставленной задачи. Причина заключается в проблемах устойчивого решения краевой задачи, «машинного нуля», вычислительной устойчивости используемых методов и т.д. Поэтому требуется искать подходы, основанные на иной интерпретации известных теорий. Одному из них и посвящена данная статья.

• 1. Постановка задачи

Рассмотрим автономную динамическую систему вида:

= fj (x) + Bj (x)uj, j=1, K• m, dt dx

—— = Ji(x),              г = m +1, ... n, dt где: t - действительная переменная; t e3 (t); 3(t) - открытое множество вещественной оси t; 3(t) = (-го, • • , + ^ ); x = (x1, . •, xn) - вектор состояния действительного n -мерного пространства; f = (J1, • K , fn ) и B = (B1, • K ,Bm ) - заданные вектор-функции; Bj Ф 0, j = 1, • к , m; u = (u1, • к ,um ) - m -мерный вектор управления; u e U; U - заданное множество допустимых управлений; m < n .

Задан терминальный функционал:

J = F [ xJT), i = m + 1, к. ,n ] ,               (2)

определенный на решениях системы уравнений (1). F - некоторая функция; T e 3 (t) .

В момент t = T могут быть заданы дополнительные условия вида h, = h; [ x(T) ] , i = 1, к. , n,               (3)

которые могут быть включены в функционал (2) через дополнительные множители Лагранжа.

Так как система уравнений (1) автономная, то множество 3 (t) допустимо сузить до отрезка [ t₀,T ] , где t₀ - начальное значение аргумента t, t₀ e3 (t) . Момент времени T не фиксирован.

Значения x(t₀) = x₀ полагаются известными.

Сформулируем задачу оптимального управления следующим образом: среди всех допустимых на отрезке [ t₀, T ] управлений u e U , переводящих точку (t₀,x₀) в точку (T ,x(T)) , найти такие, для которых функционал (2), определенный на решениях системы уравнений (1), принимает наименьшее значение при выполнении условий (3).

Введем вектор-функцию множителей Лагранжа p = (p 1 , • • , p_n ) и составим гамильтониан задачи оптимизации H :

nm

H = Ё Pif ⁺ Е P j B j u j .              ⁽⁴⁾

i = 1             j = 1

С использованием функции H в пространстве переменных D"(x,p), x e D"(x,p), p e D"(x,p), уравнения для x и p запишутся в следующей канонической форме:

dx _ д H dt д p’ dp _ д H --- — — ----. dt      д x

Отметим, что H и p на оптимальном решении непрерывны и к этому же приводит аналог условия Эрдмана–Вейерштрасса классического вариационного исчисления. Непрерывность сохраняется и в том случае, когда правые части уравнений (1) терпят разрыв.

Для оптимального управления u(t) и фазовой траектории x(t) в рамках принципа максимума необходимо существование такого ненулевого вектора p , что выполняются следующие условия [1, 2]:

• 1)    Функция H переменного u е U при каждом t е [ t₀,T ] , т.е. при

фиксированных x, p , достигает при u — u_opt (t) минимума:

^H(x opt , u opt ^, p ^{) —} mmH^(x,^u,p) . и е U

Таким образом, оптимальное управление определяется как: u_oPt — arg min H(x,u, p) .

^p          и е U

2) Выполняются условия трансверсальности:

n

H St -Z pi 5xi i — 1

T

+

t0

Г д h - д F ^ „ Z Mi— + — 5xi д xi д xi J

n

. i — 1 V

1T

— 0 , J t o

где S t, 5 x i - произвольные вариации соответствующих переменных;

M — ( M i , • к , M _n ) — вектор констант.

Обобщенные условия трансверсальности в силу независимости вариаций приводят к соотношениям:

[H ] To — 0, p i—

д F      д h i

—^{+ M} i^— д x j       д x i

i — 1, • , n .

Непосредственным следствием системы уравнений (5) и условия (6) dH д H является выполнение соотношения:---—---.

dt     д t

С учетом (9) для автономных динамических систем при незаданном явно аргументе имеем :

H — const — 0.                      (10)

Из выражений (6) для внутренних точек множества допустимых управлений получим:

5 H      ~

= Pj = °’ d uj j = °,1,K, m

Из чего следует, что формально любое управление удовлетворяет условию первой вариации функционала. Такая неопределенность порождает особый случай нахождения оптимального управления. В работе [2] доказывается, что особое управление для динамических систем вида (1) может быть найдено из соотношений:

dk faн' dtk [duj,

= 0,

k = 0,1, к ,2p s

( p s - порядок сингулярности) при выполнении следующих

необходимых условий оптимальности:

_z d d^2p s f а н )

( — 1)

5 uj ^ dt p [duj ,

P s = 0,1,2, к

> 0,

если

det

<

a ² н a u i a u j

У* °,

i , j = 1, к , m .

Из системы уравнений (11) с учетом соотношений (12) следует, что особое оптимальное управление определяется как u j osob = u j osob (x,p).

Отметим, что если в начальный момент времени значения x известны (или могут быть оценены), то вектор p определен (с точностью до констант) лишь на правом конце фазовой траектории. Возникает специфическая краевая задача, после решения которой («в принципе») тем или иным способом можно найти p(t) , а, следовательно, и u jo_{s ob} . Однако, вычислительные трудности, стоящие на этом пути, методические ошибки численных методов и ошибки округлений делают процесс нахождения достоверных значений весьма трудным, а зачастую (например, при выполнении требования реального масштаба времени) и невозможным. Поэтому представляется желательным использовать нетрадиционные методы синтеза оптимального управления, одним из которых, в частности, является метод огибающих.

Сначала докажем, что оптимальная траектория динамической системы в фазовом пространстве, определяемая в смысле минимизации функционала (2), является огибающей семейства мгновенных решений, проведенных из каждой ее точки, и что оптимальное управление может быть найдено на семействе мгновенных решений.

Представим уравнение (10) в следующем виде:

H [ x,u_opt(x, p), p ] = H(x,p) = 0 .         (13)

Введем непрерывную функцию W(x) такую, что г , 1          dW

W(x(T)) = J = F [x(T)] и p = —, и d x приведем уравнение (13) к

уравнению Гамильтона-Якоби:

H(x,p) = H

f d W ) x,—- ( d x )

= 0.

Так как функция W входит в уравнение (14) только своими частными производными, то она определяется с точностью до аддитивной постоянной W0., т.е.: W = Wp(x,a) + W0, где a = (a1, .к, an) - вектор независимых параметров, а Wp(x,a) - решение уравнения (14). Запишем уравнение гиперповерхности [3]

S = W - W_p(x, a ) - W₀

в (п + 1) -мерном пространстве переменных W,x 1 , к. ,x_n . Из-за наличия

(п +1) независимых параметров W0,a1, к.,an эта гиперповерхность является (п +1) -параметрическим семейством гиперповерхностей.

Параметр W₀ вызывает лишь сдвиг вдоль оси W , поскольку

----= - 1 * 0 . Примем:

d W o

W 0 = W 0 ( Y 1 , к , Y n )

av = av( У1.-к-Yn) V = 1, к. ,п где        y 1, - к, Yn        - параметры, такие, что dW    да

* 0, —^v ^ 0, i = 1, к. ,п, v = 1, к. ,п .

dYt

Построим огибающие относительно параметров y 1 , - к , Y _n :

д s      d W da dW^dWP да dW_{0 п}

----= >---L-> ------'---- = 0, v = 1, к. ,п.(17)

dYv Т"1! dai дYv       dai dYv

Выбором

( det

'a1-d Yv )

* 0,

функций i,v = 1, к., n .

добьемся,

чтобы

Тогда уравнения (17) будут иметь решения:

∂W

βν =     , ν =1, K, n.∂aν

С другой стороны, если W - полный интеграл уравнения (14), то по теореме Якоби имеем:

β=∂W, ∂a

∂ W p =

∂x

.

Потребуем, чтобы a и β удовлетворяли преобразованию гамильтониана H(x, p) в гамильтониан H(a) , а также каноническим уравнениям, которые, ввиду (14), запишутся как da -- dt

Из (16-20) следует,

∂ H     d β ∂ H

-    = 0,      =    = 0 .

∂β      dt  ∂a

что оптимальные траектории являются

огибающими n -параметрического семейства поверхностей.

Представим функцию W_p(x, a ) в виде суммы функций, каждая из которых зависит только от одной из переменных x ν , ν = 1, K , n , т.е.:

W = ∑ ⁿ W ν ^κ (x ν , a ) + W 0 .

ν = 1

Определим канонические переменные p ν , ν = 1, K , n :

∂ W ∂ W ^κ (x , a )

• p _ν =      = ^{ν ν} , ν = 1, K , n .

∂xν       ∂xν

Согласно выражениям (22), переменные   pν , ν = 1, K , n оказываются функциями только одной xν и a, в то время, как уравнения (1), (5), (19) говорят о том, что pν , ν = 1, K , n в общем случае должны быть функциями всех x1 , K , xn и остальных pi , i = 1, K ,n, i ≠ν . Это противоречие может быть устранено, если приравнять aν , ν = 1, K , n некоторые определенные комбинации переменных x1 , K , xn , «замороженных» в данный момент времени, т.е.:

a_ν = a_ν (x₁, K ,x_n), ν = 1, K ,n .             (23)

Из выражений (16), (19), (22), (23) следует, что p1 , K , pn и управление uopt, можно определить на параметрическом семействе поверхностей, которое огибает оптимальная траектория, если в качестве параметров γ1 , K ,γn соответствующим образом взять фазовые координаты, а уравнения (17) будут разрешимы относительно частных производных Wp по параметрам a1 , K , an . Фиксируя в качестве параметров «замороженные» в текущий момент времени значения фазовых координат, мы тем самым на семействе поверхностей определим семейство кривых. Назовем их мгновенными решениями, поскольку они определяются функцией Wp, являющейся решением уравнения (14).

В рамках решения уравнения (14) можно использовать в качестве мгновенных решений произвольные заданные функции, удовлетворяющие условиям (17), (19) - (23).

С другой стороны, соотношения (18)-(23) говорят о том, что для построения мгновенных решений можно следующий подход, а именно производить условное разделение переменных в уравнении Гамильтона-Якоби (см. [3]).

Отметим, что мгновенные решения должны удовлетворять условию минимизации функционала (2) относительно используемых параметров.

Таким образом, оптимальная траектория динамической системы в фазовом пространстве является огибающей семейства мгновенных решений, проведенных из каждой ее точки.

Представим уравнения (5) для p = (p 1 , ..., p n ) в следующей форме:

dp _v _ д H dt д x _v

(д f 8 B_v ) + ^v • u _v

₍ 8 x_v 8 x_v     ,

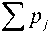
j _ 1 J * v

^д f /^B

8 xv   8 xv

-

2 p. f i _ m + 1 д X v

n

v _ 1, ... , m

Преобразуем это уравнение к виду:

dp ' ⁺ Ф у p _v ^_ G v    ^{v _} 1, ... ,m ,

dt где: Фу

'f + ^- • u.), О,           + • ul- £ p.^f-

(д xv 5 xv J 1 j (5 Xv 6 Xv j J . _m++1 5 Xv j *v

Проинтегрировав уравнение (25), получим:

p v _ exp( - J Ф v dt) | J G v exp( J Ф v dt) - C v J v = 1, -к ,m , (26)

Постоянные     Cv , v = 1,. к, n находятся из условий трансверсальности (9).

Первоначально рассмотрим случай, когда порядок сингулярности равен единице. Тогда особое управление можно найти из системы уравнений (см. [2]):

dpd pj_ 0,       _ 0,        _ 0, j _ 1, K. ,m.(27)

j dtdt

Из первых двух уравнений системы (27) следует, что G j = 0 .

Разрешим это уравнение относительно переменной xj . Если корень существует, то:

X j = n j (X v ,P v ; V = 1,... ,n; v * j) .           (28)

Тогда третье уравнение системы (27) после преобразований запишем как:

dGj dt

5 Gj

—- \ f. + В и ^)+

5 X ^j j josob'

d G j d n j ------------------•---------------- dn j dt

= 0.

Из последнего соотношения можно найти особое управление:

u. _K = j osob

f) +

G jn J/d G d n j dt J/ d x j

при выполнении необходимых условий оптимальности в следующей форме:

d G, Bj     j d xj

< 0, j = 1,..., m .

^x j = n j

Отметим, что корень уравнения G j = 0 необязательно может быть единственным. Тогда каждый корень проверяется на выполнение необходимых (30) и достаточных (2) условий оптимальности.

Отметим также, что на мгновенном решении X j = const = n j .

В случае нулевого порядка сингулярности pj (см. (26)) либо сохраняет знак, либо становится равным нулю лишь в одной точнее на конце отрезка. Дополнив условие pj = 0 условиями первого порядка сингулярности, мы приходим к аналогичному выражению.

В случае, когда порядок сингулярности превышает единицу, то, выделив условие сингулярности первого порядка Gj = 0, или, соответственно, xj = nj, а затем, продифференцировав его 2 ps -1 раз, можно найти особое управление как:

u j osob

= f ^x-n_] v

d n j       d² p 1 n j

,1^, K ’ dt² p -¹

A

)

Следовательно, особое оптимальное управление в рамках заданного терминального критерия оптимальности можно найти на семействе мгновенных решений.

Заключение

Обобщая полученные выше результаты, можно сделать следующие выводы:

• 1)    оптимальную траекторию динамической системы в фазовом пространстве можно представить как огибающую семейства мгновенных решений, проведенных из каждой ее точки;

• 2)    оптимальное управление может быть найдено на семействе мгновенных решений из конкретных соотношений, складывающихся на тот или иной момент времени.