Метод соединения внутренних и внешних асимптотик в задачах математической физики

Введение1

Принципиальной особенностью асимптотических методов является локальность получаемых с их помощью решений [1–3]. При этом в сложных задачах зависимость от малого параметра редко бывает линейной. Источники нелинейности, как правило, локализованы. Места концентрации сильных нелинейных эффектов усиленно изучаются в теории разрушения, гидродинамике обтекаемых тел, гиперзвуковой аэродинамике и других областях прикладной математики [4–7]. Неравномерность асимптотических разложений в окрестности таких мест значительно затрудняет оценку и анализ локальнонелинейных асимптотик.

Публикация подготовлена при финансовой поддержке Минобрнауки (базовая часть государственного задания по научным исследованиям высших учебных заведений № 2014/66, код проекта 1281, рег. № 114123040133).

^∗ Статья написана по материалам международного симпозиума "Дифференциальные уравнения. Сто лет математической науке Урала". Пермь. 16–19 мая 2016.

Использование асимптотического ряда в качестве приближения в окрестностях особенностей всегда приводит к необходимости определения числа членов разложения адекватно приближающих искомое решение. Существует много подходов к этим задачам [8]. Метод аналитического продолжения (например, преобразование Эйлера £ = £ (1 + £ ) ^{- 1}, или растяжения координат в локальной области) требует знания области единственности разложения искомой функции малого параметра ε [9–12]. Эти методы полезно применять, когда известно большое количество членов ряда разложения. Тогда становится возможным выполнить, зная области единственности разложения, аналитическое продолжение, пользуясь, например, диаграммой Домба–Сайкса [8, 13].

Для применения методов обобщенного суммирования [8] необходимо также знать значительное количество членов ряда разложения. На практике в этих рядах обычно известны 3–5 компонентов и именно из этого сегмента ряда приходится извлекать имеющуюся информацию. Для этой цели может быть очень полезен метод Паде-аппроксимант [1, 2, 12–17]. Паде-аппроксиманта (PA) выполняет мероморфное продолжение функции, заданной в виде степенного ряда и по этой причине позволяет достичь успеха в случаях, когда аналитическое продолжение применить нельзя. Если РА сходится к заданной функции, то корни в его знаменателе стремятся к сингулярным точкам.

В математической литературе исследовались, главным образом, одноточечные дробно-рациональные PA [16, 19]. Двухточечные аппроксимации Паде (TPPA), соединяющие асимптотики в переходных слоях, использовались лишь в отдельных прикладных задачах [2, 13, 14]. Ранее в работах [4, 5] был предложен и эффективно применен на примерах функций Эйри и Блазиуса метод соединения внутренней и внешней асимптотик с помощью кусочно-монотонной интерполяции [6] и с условиями гладкости в переходной области [7]. Затем в работах [10, 11] данный метод был использован для немонотонной интерполяции, в качестве которой применяется TPPA с условием тривиальности для кривизны в точке максимума.

В настоящей работе систематизируется и методологически обосновывается процедура применения соединения асимптотических разложений в задачах математической физики и обтекания плоской пластины гиперзвуковым потоком реагирующего газа.

• 2.    Применение двухточечных Паде-аппроксимант в краевых задачах

Для решения краевых задач будем использовать гипотезу о существовании двух асимптотик, для двух предельных значений параметра. Наиболее часто при этом используется метод сращиваемых асимптотических разложений (Matching method) [8]. При этом оперируют понятиями внутренней и внешней асимптотик, действующих в областях £ ^ 0 и £ ^ да . Однако для корректного применения метода сращивания необходимо знать точку сращивания или, по крайней мере, область перекрытия асимптотик. Точное описание всего переходного слоя 0 <  £ < да существует лишь в тех случаях, когда имеются специальные функции типа функции Эйри, связывающие в один узел разное поведение решений по обе стороны слоя.

Для соединения неперекрывающихся асимптотик в последнее время интенсивно разрабатывается метод, опирающийся на TPPA [6, 7, 13, 18, 20, 21]. В работах [1, 5, 7]

таким путем построены температурные профили в пограничном слое газа. В последующих работах [10, 11] метод хорошо зарекомендовал себя при исследовании теплообмена в гиперзвуковом пограничном слое.

В работах [6, 17] метод соединения асимптотик применяется к пограничному слою в реагирующем газе, а в работах [4, 15] – к слою Кнудсена в разреженном газе. Метод соединения использовался в исследовании устойчивости развивающегося слоя Экмана на вращающейся пластине [22].

Двухточечные Паде-аппроксиманты вводятся следующим образом:

пусть существуют внутренняя асимптотика

^(£) = 2 а£, £ ^ 0

i = 0

и внешняя асимптотика да ре(£) = 2ei£-, £ >z .(2.2)

i = 0

Тогда функция mn фтп (£) = 2а£ 2bk£k(2.3)

к=0

будет называться двухточечной Паде-аппроксимантой асимптотических разложений (2.1), (2.2). Коэффициенты α _л , β _k определяются так, что первые р коэффициентов правильной части разложения функции (2.3) в ряд Лорана совпадают с коэффициентами (2.1), а (m+n+2-p) коэффициентов главной части ряда Лорана совпадают с коэффициентами (2.2). Рассмотрим в качестве примера применения TPPA краевую задачу Эйри [8]:

у " - Л² xy = g ( x ) y , у (0) = 1, у ( да ) = 0, Л >>  1.

(2.4)

Асимптотическое решение имеет вид [14]

у ( x ) = U ( $ )1 + O ( Л -¹) ] , $ = хЛ\ ⁽².5)

U ( ξ ) – функция Эйри, определяемая из

U"- $U = 0,

U (0) = 1, U ( да ) = 0, Л >>  1.

(2.6)

Переходный слой задается областью 2

x = cЛ ³ , c * = const .

Внутренняя область переходного слоя:

x e [ 0, x - ( Л ) ], x - = o ( Л ) .

Внутренняя асимптотика функции Эйри:

У + у у" = 0; T " + ayT' + а а = 0;

U = 1 - a£ + ¹ £ ³ + O ( £ ⁴), £ ^ 0, 6

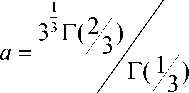
0.7290.

(2.7)

Внешняя область переходного слоя:

-2/ x e [x +, w),x + = O(A /3).

Внешняя асимптотика функции Эйри:

-V          3/^

U = b£ ^/4exp l- -£ ² lx

5 —3/         a x1 -   £   + O(£ ), £

_   48               _

Паде-аппроксиманта:

(2.8)

У + 2 —T 'X J = 0; J J- yc ‘= 0;

i = 1                                        (3.¹)

J = - —с; ; X c = 1, a      i = 1

где y ⁽ Q ) = ^T/ xx ; q = ^{n 2} V x ; ^ ⁽ ? ) = dy ; ;

0 T

T = T ( q ) ; a = M\к - 1)/4 ; T- функция тока, T ( q ) - безразмерная температура, Ji - безразмерная плотность диффузионного потока концентрации компоненты i , c i - без

1 - a£ + 2 £¹ - 2 a£ ³ + ³² a£⁴

33  5

U                    a 17/

1 + 32 a £ /4

5 b

x

(2.9)

x exp

-

к

Э 3 A з £2.

Аппроксимация функции Эйри (2.9) сохраняет по три члена асимптотик (2.6)–(2.8) на обоих концах и обеспечивает хорошую точность внутри слоя. Специфика краевой задачи учитывается в форме модифицированной TPPA – умножая ее на добавочную функ- 2³

цию exp( - у £ ²) , мы обеспечиваем "мягкий" выход на асимптотики при 0 <  £ < w вплоть до полного совпадения с ними в граничных точках области.

размерная концентрация компоненты i , а - число Прандтля, Le – число Льюиса, М – число Маха, к - показатель адиабаты. Граничные условия на поверхности пластины:

у (0) = у' (0) = 0 ; T (0) = T s ;

С 1⁽ О ) = c S ; y ^{( w )} = 2 ; ^{T ( w )} = 1 ;    (3.2)

^C 1^{( W )} = ^c 10 ; c 2^{( w )} = c 20 .

Внутренняя асимптотика при q ^ 0 :

у = a 2 Q ² + O ( q ⁴) ;

T = T_s + T 1 Q - 2 aaa 22 q ² + O ( q ) ;    (3.3)

^C 1 = ^C 1 S ^{+ C} 11 ^{Q +} O ^{( q} ).

Внешняя асимптотика при q ^ w : ln(y”) = -q 2 + CQ + ln A + О(1) , ln( - C ) = -2 — + ln B{ + o (1).

¹          Le ₁        ¹

(3.4)

Решение краевой задачи (3.1)–(3.2) аппроксимируем, соединяя асимптотики (3.3) и (3.4) Паде-аппроксимантами:

ϕ _a

3. Теплообмен в пограничном слое реагирующей смеси газов

Рассмотрим установившееся ламинарное течение в сверхзвуковом пограничном слое бинарной смеси газов в условиях отсутствия массовых сил, термо- и бародиффузии и излучения. Будем предполагать, что течение смеси является "химически замороженным", т. е. изменение концентрации компонент в пограничном слое происходит за счет их конвекции и диффузии. Тогда автомодельные уравнения при ^ = T имеют вид [6, 17]

= ²¹

к

T = a

—

⁽¹ + A Q ^3)ex p ^{( -} Q ² + ^C Q )

1 + a1Q + a2q2 + 4q4 7

ς _m

- Q

в 0 + вб

exp ( - — ( Q ² - c q ) ) ,

,

(3.5)

c

= C ,, ^{1 +} / ^{+ YQ 2}2 exp( - 2 ^— q ).

^{1 +} Y 2 Q          L^

(3.6)

Следуя методике [6, 10, 17], определим параметры Паде-аппроксимант (3.5)–(3.7), используя асимптотические разложения (2.3), (2.4)

a1 = a 2 + c;a2 = a 2 + ca 2

—

ςm     cσςm в0 = T ; P1 =  „

T ₁           T ₁

-

c ²

^T 1 ^,

—

1;

2 a ( Le, - a )           2o²

—²—¹---- , Y 2 =---5------- .

Le 1 - 2o        Le₁(1 - 2a )

(3.7)

При g ^» три члена в асимптотике (3.4) обеспечиваются, если положить в = .

1 B

Граничные условия (3.2) удовлетворяются, если принять ςς

Ф а = J Ф ‘ dQ; T a = T S + J T a dQ ^;

00 ς c1 a = cS 1 + J cidS'; c2a = 1 - c1 a •

(3.8)

Интегральные условия (4.8) дополним нормирующими соотношениями

Ю                         TO

• ¹    = TS + J T a ds; c 10 = c S 1 + J c [ a^d S •    (3.9)

и интегральными соотношениями, полученными на основании совпадения Паде-аппроксимант (3.6) с точностью до трех членов во внутренних разложениях (3.3), (3.4):

• 1    TO           'V 7Л_ 'V

a 2 = 2 { Ф [ ^{2 -} Ф Л’c = { [ ^{2 -} Ф Г • (3.¹⁰⁾

Используя внешнее разложение, получим интегральное соотношение для А : умножим первое уравнение системы (3.1) на exp( g ² - cg ) , проинтегрируем от 0 до to , вычисляя интеграл от первого члена уравнения по частям с учетом (3.4), получим

A = 2 a ₂ - j ( p - 2g + cф '' exp( g ² - cg ) dg. (3.11) 0

Аналогично из второго уравнения системы (3.1) с учетом (3.4) получим интегральное соотношение для B :

B = a J T ( ф - 2 g + c ) exp( a ( g ² - cg )) dg 0

+ TO ( aa^ '' ² - Tc ‘ ( Le , - Le ₂)) x             (3.12)

• ^exp^{( a (} g ^{2 -} cg )) dg ^- T

Интегральное соотношение для B ₁ получим, умножая третье уравнение (3.1) на величину _exp ( ^{2 σ} _ς ) и интегрируя полученное Le ₁

выражение от 0 до to , с учетом (3.4):

о f ^f 2 a p   _z2 a

B 1 =J ф ,    ^c 1 ^exp⁽—) dg.

Le       Le

(3.13)

Априори при больших значениях числа Маха известно, что распределение температуры имеет максимум вблизи стенки в точке ς _m .

Таким образом, из уравнений (3.1) сле- дует очевидное условие:

T "(g_m ) = - aap"²(g_m ) . (3.14) Подставляя в (3.14) производную аппрокси-манты из (3.6), получим условие для определения точки экстремума ς _m . Так как через величину В распределение концентраций оказывает влияние на распределение температуры, а вычисление В показывает зависимость от верхнего предела интегрирования, то условие, полученное из (3.14) служит средством контроля при выборе верхнего предела интегрирования для В.

Полученные результаты

Обсуждение. Задача была решена для эффективной бинарной смеси газов CO + O ₂ + N ₂ + CO ₂, причем ввиду близости молекулярных масс CO , O ₂ , N ₂ эти компоненты объединялись в одну группу (сопровождаясь индексом 1), а компонента CO ₂ представляла вторую группу (с индексом 2). В предположении химически замороженного течения предполагалось, что концентрация азота остается постоянной, а гомогенная реакция протекает по схеме Вулиса: 2 CO + O ₂ = 2 CO ₂ .

Расчеты проводились при числах Маха М =5; 10, числе Прандтля a = 0,72, числах Льюиса Le₁ = 1,2 ; Le ₂ = 1,3 .