Метод согласования результатов оценки стоимости, основанный на нечеткой логике

Значение НЕ-факторов в оценке стоимости объектов

Профессиональные оценщики постоянно сталкиваются с проблемами недостаточной адекватности получаемых оценок, причины которых кроются в значительной доле дефектов в имеющихся данных, а также в том, что зачастую информация об объектах оценки не является исчерпывающей. «Белые пятна» в исходной информации и возможностях ее обработки с помощью различных методов оценки, по существу, являются НЕ-факторами.

Термин «НЕ-факторы» был предложен А.С. Нариньяни для комплекса свойств, характерных для реальной системы знаний, но плохо представленных в формальных системах (неполнота, неточность, недоопределенность, некорректность, нечеткость и т. д.) [19, 20]. Учет НЕ-факторов при оценке стоимости дает возможность более полного использования информации, не явно содержащейся в исходных данных, за счет преобразования ее в форму, доступную для обработки, что позволяет увеличить точность и согласованность результатов оценки, а также повысить степень доверия к этим результатам.

В настоящее время в области оценки стоимости объектов принято учитывать только неопределенность, неточность, недоопределенность и нечеткость . Другие виды НЕ-факторов учитываются редко, среди них такие, как «неполнота» и «противоречивость» (не-непротиворечивочивость), без учета которых зачастую невозможно повышение качества оценивания. В таблице 1 представлены примеры учета НЕ-факторов в оценке стоимости.

Рассмотрим некоторые НЕ-факторы более подробно.

Термин « неопределенность » наиболее часто используется в публикациях, посвященных оценке стоимости объектов, в двух смыслах. В узком смысле он означает, что значение некоторой величины может быть получено с некоторой вероятностью. В широком смысле под неопределенностью подразумевается наличие одного или нескольких НЕ-факторов. Например, в Методических рекомендациях по оценке эффективности инвестиционных

Таблица 1

Учет НЕ-факторов в оценке стоимости

НЕ-фактор	Примеры исследований
Неопределенность (в узком смысле)	По мнению Л.А. Лейфера, «В зависимости от метода, используемого в процессе оценки, от характера исходных данных и источника их получения интервал неопределенности может определяться по-разному. Он может основываться как на статистической методологии, если факторы неопределенности имеют вероятностную природу (по аналогии с расширенной неопределенностью типа А), или на методологии нечетких множеств или методах интервальной математики, если природа факторов неопределенности такова, что не может быть описана вероятностными моделями (по аналогии с неопределенностью типа В)» [16] П.Л. Виленский, В.Н. Лившиц и С.А. Смоляк отмечают, что «неопределенность нельзя трактовать как отсутствие какой бы то ни было информации об условиях реализации проекта, речь может идти только о неполноте и неточности имеющейся информации. Соответственно, учет неопределенности подразумевает сбор и наиболее полное использование всей имеющейся информации о возможных условиях реализации проекта и «степени их возможности» (не будем пока конкретизировать этот термин, укажем лишь, что мы применяем его и тогда, когда неопределенность не носит вероятностного характера). Иными словами, упор делается не на отсутствие, а на наличие информации» [9]
Недоопределенность
Нечеткость
Неточность	По мнению И.Д. Грачева и Е.В. Елисеевой, «уровень случайной составляющей ошибки оценивания рыночной стоимости недвижимости можно определять согласно общей теории измерений – методом параллельных измерений. Авторами исследованы разные данные (отчеты) об оценке одних и тех же объектов недвижимости, выполненные разными агентами. Получены среднеквадратическое отклонение и средняя погрешность оценок» [10] П.Л. Виленский, В.Н. Лившиц и С.А. Смоляк полагают, что «неопределенность нельзя трактовать как отсутствие какой бы то ни было информации об условиях реализации проекта, речь может идти только о неполноте и неточности имеющейся информации» [9].
Неполнота	По мнению Г.Г. Азгальдова и Н.Н. Карповой, «Качество тех немногочисленных квалиметрических методик, которые реально используются на практике, в подавляющем большинстве случаев является чрезвычайно низким. В основном это связано с тем обстоятельством, что из-за незнания теории квалиметрии разработчики квалиметрических методик зачастую недопустимо упрощенно решают стоящую перед ними задачу. В связи с этим полученные на основе их разработок количественные оценки качества имеют крайне низкую степень достоверности, не позволяющую использовать их в сколько-нибудь серьезных техникоэкономических расчетах» [5] (см. также [9])
Противоречивость	По мнению А.В. Нестерова, «сегодня законодательство, регулирующее оценочную деятельность в России, представляет собой пять противоречивых и не очень ясных документов, а именно: •    Федеральный закон Российской Федерации «Об оценочной деятельности в Российской Федерации» •    Федеральный закон Российской Федерации «О лицензировании отдельных видов деятельности». 1998 г. •    Постановление Правительства Российской Федерации от 11 апреля 2001 г. № 285 «О лицензировании оценочной деятельности» •    Постановление Правительства Российской Федерации от 6 июля 2001 г. № 519 «Об утверждении стандартов оценки» •    Федеральный закон Российской Федерации «О лицензировании отдельных видов деятельности». 2001 г. » [21]

проектов [17] под неопределенностью понимается неполнота и неточность информации об условиях реализации инвестиционных проектов. Другим примером является трактовка неопределенности Ф.Х. Найтом [18], которая включает в себя неполноту и неоднозначность рыночных отношений.

Неточность значения означает, что его величина может быть получена с точностью, не превышающей некоторый порог, определенный природой соответствующего параметра объекта.

Недоопределенность величины означает, что она по своей природе является более точной, чем позволяет установить доступная в конкретный момент времени информация об объектах.

Нечеткость предполагает отсутствие точных границ множеств объектов. Для формализации этого НЕ-фактора Л. Заде предложил использовать нечеткие множества [2], которые позже легли в основу нечеткой логики [3]. В настоящее время термин « нечеткая логика » используется в двух смыслах:

• 1)    в узком (формально-логическом) – как специальный раздел многозначной логики;

• 2)    в широком (инженерном) – как конкретный набор теорий, включающий лингвистические переменные, нечеткие множества, приближенные рассуждения, нечеткое управление, а также обобщенные ограничения, гранулярные вычисления и вычисления со словами, играющими роль меток гранул.

Понятие « неполнота » может трактоваться по-разному. Чаще всего неполнота характеризуется отсутствием необходимой для решения задачи информации [23]. При формальном исследовании этого НЕ-фактора с использованием классических логических систем рассматривают свойство полноты , которое обычно формулируется следующим образом [14]: для множества формул с заданными свойствами исходная система аксиом и правил вывода должна обеспечить вывод всех формул, входящих в это множество.

В области искусственного интеллекта применяются формулы в виде конструкции предикат – аргумент [11], синтаксис которых можно представить так:

<утверждение> :: = <предикат>(<аргумент>, … ,<аргумент>).

Здесь применима следующая формулировка свойства полноты в терминах системы утверждений [12]:

• •    все истинные утверждения, которые формулируются на языке некоторой системы утверждений, могут быть доказаны в этой системе (семантическая полнота);

• •    присоединение к некоторой системе утверждений в качестве аксиомы какого-то недоказуемого в ней утверждения ведет к противоречию (синтаксическая полнота).

Также существуют различные трактовки понятия « непротиворечивость ». Как отмечено в работе [12], закон противоречия впервые сформулировал Аристотель, который утверждал: «Невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении» [6]. С формальной точки зрения, противоречия – это аналитически ложные положения, представляющие собой «логическую ложь» при произвольной предметной интерпретации логических переменных, а поэтому неспособные выражать объективные истины. В классических логических системах свойство непротиворечивости сводится к тому, что исходная система аксиом и правил вывода не должна давать возможность выводить формулы, не принадлежащие заданному множеству с выбранными свойствами [14].

В логике формулируют четыре смысла непротиворечивости:

• •    непротиворечивость относительно отрицания;

• •    тривиальная непротиворечивость;

• •    непротиворечивость в смысле Поста [1];

• •    семантическая непротиворечивость.

Следует отметить, что непротиворечивость может рассматриваться как частный случай полноты, которая в этом случае понимается как неполнота в широком смысле [14].

Также известны различные более узкие трактовки полноты и непротиворечивости.

Следует отметить, что НЕ-факторы связаны между собой. Например, в работе [20] связи между НЕ-факторами рассмотрены на примере неоднозначности , которая рассматривается как группа НЕ-факторов, сходных по своей форме. В этой работе А.С. Нариньяни выделено три группы оценок, связанных с неоднозначностью, а именно:

• •    адекватность альтернатив;

• •    возможность/вероятность правильного выбора;

• •    модальные оценки альтернатив (желательность, допустимость, необходимость и т. д.).

Традиционно в области оценки стоимости используются вероятностные модели, которые, по существу, способны учитывать связи НЕ-факторов «неопределенность», «неточность» и «недоопределенность». При этом учитываются только явные или скрытые свойства исходных данных, которые имеют вероятностную природу. В случаях когда исходные данные не полностью достоверны, вероятностные модели требуется дополнять другими, способными учитывать степень уверенности оценщика в имеющихся у него исходных данных.

Применение нечеткой логики в процессе оценки стоимости позволяет не только учесть достоверность исходных данных, но и связи между нечеткостью, неточностью и недоо-пределенностью. Такие связи могут быть учтены в процессе построения функций принадлежности [2]. В тех случаях когда известна информация о стоимостных ограничениях, выраженных путем указания некоторых пороговых значений или в виде интервалов, возможно использование этой информации для построения кусочно-линейных функций принадлежности.

Кусочно-линейная функция – это функция, определенная на множестве вещественных чисел, линейная на каждом из интервалов, составляющих область определения. Примерами кусочно-линейных функций принадлежности являются треугольная и трапециевидная функции принадлежности.

Треугольная функция принадлежности определяется тройкой чисел ( a , b , c ), и ее значение в точке x вычисляется согласно выражению:

(x - a)/(b - a) ,a < x < b pA (x ) = ■!( c - x)/(c - b) ,b < x < c

0 , в остальных случаях

Трапециевидная функция принадлежности определяется четверкой чисел ( a , b , c , d ), и ее значение в точке x вычисляется согласно выражению:

(x - a)/(b - a) ,a < x < b pA(x)=<

1 ,b <  x <  c

( d - x )/( d - c ) , c <  x <  d

0 , в остальных случаях

В случае использования треугольной функции принадлежности, чтобы получить результат оценки стоимости в виде диапазона стоимостей P ∈ [ P ₁, P ₂] или конкретного значения стоимости P , требуется провести операцию дефаззификации . При этом для определения диапазона стоимостей можно использовать информацию о том, с какой степенью достоверности k требуется получить результат. В процессе дефаззификации коэффициент k может быть использован для построения усеченной функции принадлежности так, как показано на рисунке 1. Результатом будет диапазон стоимостей, на котором усеченная функция принадлежности будет принимать максимальное значение, а именно P ∈ [ k ( b – a ) + a , c – k ( c – b )]. Для определения конкретного значения можно использовать метод «центра тяжести» («центра масс») (рис. 2). Результатом будет значение P = ( a + c )/2 + k( c – a )/4.

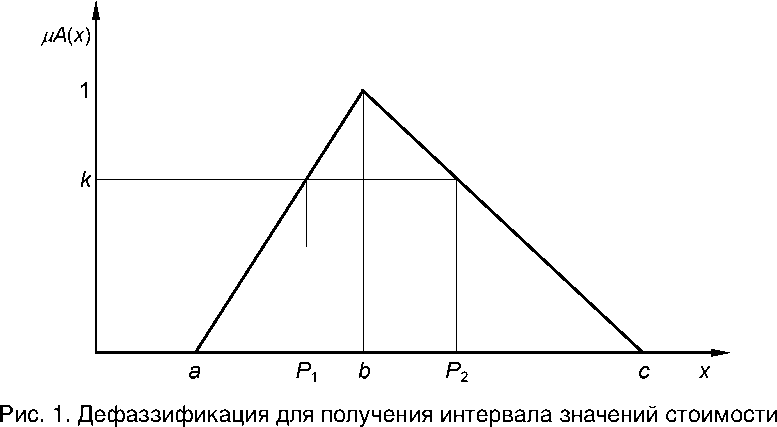
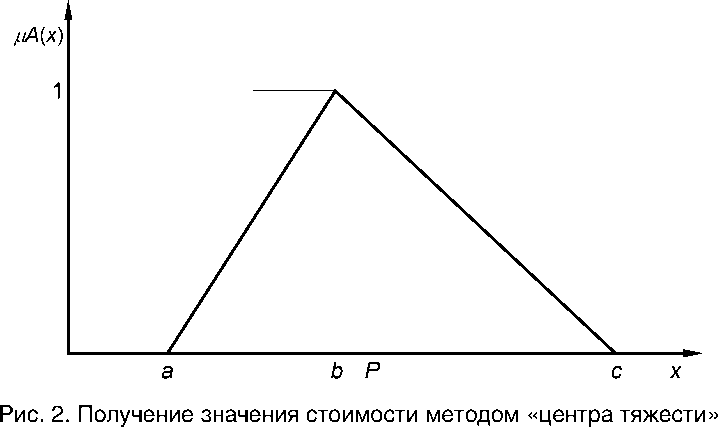
Аналогичным образом могут быть получены результаты оценки стоимости на основе ограничений в случае использования трапециевидной функции принадлежности, а также любой другой кусочно-линейной функции принадлежности. При этом информация о точности исходных данных выражается в виде ограничений, о достоверности исходных данных – с помощью коэффициента k при усечении функции принадлежности, а в процессе получения результатов используется скрытая информация о связи ограничений с достоверностью исходных данных.

Модель и методы оценки стоимости энергосберегающей технологии

Примеры моделей расчета рыночной стоимости энергосберегающей технологии¹ (далее – объект оценки) с использованием доходного подхода построены на основе реального отчета об оценке стоимости, выполненного одним из авторов. Доходный подход был выбран, поскольку он наиболее достоверно отражает действительную ценность нематериальных активов [13]. Классификация принципов формирования стоимости, представленная в работе [15], послужила основой для извлечения и анализа исходных данных об объекте оценке с целью определения параметров стоимостных моделей. Изменяемые во времени параметры моделей, которые необходимы, так как связаны с принципом ожидания и принципом изменения стоимости во времени, обладают наибольшей неопределенностью по причинам их нестабильного (слабо прогнозируемого) или неэкономического характера, отсутствия в достаточном объеме данных, требуемых для анализа значительного временно ́ го периода.

Рассмотрим особенности построения расчетных моделей стоимости объекта оценки. В рамках доходного подхода основными укрупненными параметрами стоимостных моделей явились ставка дисконтирования ( d ) и денежный поток ( CF ), которые основаны на фактических и прогнозных показателях доходов (выгод) и расходов от использования и (или) владения оцениваемой технологией. В качестве метода оценки стоимости был выбран метод дисконтированных денежных потоков (метод дисконтирования экономии затрат, метод выигрыша в себестоимости и метод «экстраполяции лицензионных платежей»), который в обобщенном виде может быть представлен следующим образом:

_w ^ -1    CF i      CF n + Rev

p      (1 + Dif°, 5 +(1 + Dn) n "0,5, где Vp – стоимость объекта оценки, рассчитанная на основе доходного подхода;

CF_i – поток выгод (денежный поток) в i -м году;

CF_n – поток выгод (денежный поток) в последний прогнозный период;

• i    – порядковый номер года получения выгод от использования нематериального актива;

• n    – количество прогнозных лет (периодов) – определяется экономическим сроком жизни объекта;

Rev – « реверсия» (или «терминальная стоимость») – капитализированный денежный поток в постпрогнозном периоде (если прогнозный период совпадает со сроком экономической жизни объекта, то Rev = 0);

D_i – ставка дисконтирования в i -м году.

По состоянию на дату оценки были выявлены три основные отрасли экономики, в которых оцениваемый объект использовался и приносил выгоды: строительная отрасль, энергетика и жилищно-коммунальное хозяйство (далее – ЖКХ). Анализ применения оцениваемой технологии показал, что эффекты от ее использования создаются за счет владения и (или) использования следующими участниками рыночных отношений (которые и являются потенциальными лицензиатами и (или) приобретателями прав на оцениваемую технологию):

• •    предприятия – производители тепловой и электрической энергии;

• •    строительные организации (инвесторы – девелоперы);

• •    предприятия – балансодержатели объектов строительства.

Прогноз денежных потоков был основан на результатах маркетинговых исследований, целевых ориентирах развития проекта, а также на прогнозах развития внешней среды, экономики страны и отраслей (строительство, энергетика, ЖКХ), в которых используется (или могла бы использоваться) запатентованная технология. Неопределенность в исходных данных и прогнозных показателях учитывалась с помощью построения нескольких сценариев развития внешней среды и деятельности компании-правообладателя. При этом мерами экономического дохода служили [22]:

• •    доходы, полученные за счет увеличения выручки, относящейся к объекту оценки (оцениваемая технология позволяет увеличить объем продаж тепловой энергии при тех же затратах на ее производство);

• •    доходы, полученные за счет сокращения расходов, относящихся к объекту оценки (снижение затрат на подготовку инженерной инфраструктуры – получение технических условий; снижение затрат на отопление введенных в эксплуатацию площадей; снижение затрат на производство 1 Гкал тепловой энергии);

• •    доходы, полученные за счет сокращения объема инвестиций, относящихся к объекту оценки (оцениваемая технология позволяет снизить инвестиции в строительство тепловых магистралей при уплотнительной застройке или реконструкции, особенно в исторических центрах крупных городов, где существует дефицит тепловых мощностей и физически невозможна или нецелесообразна прокладка новых тепловых магистралей).

При определении ставки дисконтирования были рассмотрены основные источники рисков (риск неудачного продвижения продукта на рынок; риск высоких расходов; риск неэффективных инвестиций; общеэкономические риски) и способы их минимизации. В результате были разработаны три расчетные модели стоимости объекта оценки (см. табл. 2), в которых денежные потоки были построены на основе реальных экономических эффектов.

Таблица 2

Расчетные модели стоимости объекта оценки

Модель 1 выгоды создаются за счет использования объекта оценки в строительстве, ЖКХ и ТЭЦ	Положительные эффекты и доходы в строительстве создаются за счет экономии затрат в инженерную инфраструктуру при снижении подключаемой мощности с 120 до 80 Гкал на 1 миллион квадратных метров В ЖКХ положительные эффекты и доходы получаются от снижения затрат на отопление объектов, построенных с использованием оцениваемой технологии, в размере 0,04 Гкал/м2; У ТЭЦ положительные эффекты и доходы получаются за счет снижения себестоимости производимого тепла, увеличения отпуска тепловой энергии при неизменных затратах на ее производство, а также за счет высвобождаемого условного топлива за счет увеличения удельной выработки электрической и тепловой энергии
Модель 2 генерирование выгод происходит за счет владения объектом оценки	Патентообладатель продолжает получать лицензионные платежи на тех же условиях, что и за исторический период. При этом базой для расчета лицензионных платежей являются результаты специальных маркетинговых исследований (прогноз вводимых площадей на период действия исключительных прав) и расчеты удельных паушальных платежей, определенных методом сравнения продаж на дату оценки из расчета за 1 квадратный метр строящегося или проектируемого по оцениваемой технологии здания (сооружения)
Модель 3 генерирование выгод происходит за счет владения объектом оценки	Патентообладатель продолжает получать лицензионные платежи на тех же условиях, что и за исторический период (не учитываются планы и прогнозы патентообладателя, а также возможность принимать управленческие решения). Денежные потоки построены на базе тренда исторических платежей

В зависимости от методов, используемых профессиональными оценщиками в процессе оценивания рыночной стоимости, от характера исходных данных и источника их получения итоговое значение стоимости и интервал неопределенности могут определяться по-разному. Интервал неопределенности может основываться на статистической методологии, если факторы неопределенности имеют вероятностную природу, или на методологии нечетких множеств, если природа факторов неопределенности такова, что не может быть описана вероятностными моделями [16]. Рассмотрим оба варианта.

Статистический метод согласования результатов

В результате проведенных расчетов для каждого сценария трех моделей получены тридцать два значения рыночной стоимости на дату оценки методом дисконтирования денежных потоков (далее – ДДП, см. рис. 3).

Как видно из таблицы 3, оценка в рамках доходного подхода с использованием метода экономии затрат и выигрыша в себестоимости (модель 1) показала, что стоимость объекта оценки находится в диапазоне от 103 до 189 условных единиц (у. е.).

Таблица 3

Результаты расчетов для модели 1

Описание параметра	Результаты оценки стоимости, у. е.
	для пессимистического сценария	для оптимистического сценария
Сценарий 1 (захват рынка – 0,19%, ежегодный рост доли – +15%, выделение эффекта – 25%, Dmin = 33%, D = 36%) max	103	115
Сценарий 2 (захват рынка – 0,30%, ежегодный рост доли – +16%, выделение эффекта – 25%, Dmin = 33%, D = 36%) max	169	189
Сценарий 3 (тренд-прогноз по фактическим данным, выделение эффекта – 25%, Dmin = 33%, Dmax = 36%)	152	170

Таблица 4

Результаты расчетов для модели 2

Описание параметра	Результаты оценки стоимости, у. е.
	для пессимистического сценария	для оптимистического сценария
Сценарий 1 (захват рынка – 0,19%, ежегодный рост доли – +15%, D min = 33%, D max = 36%)	232	256
Сценарий 2 (захват рынка – 0,30%, ежегодный рост доли – +16%, Dmin = 33%, Dmax = 36%)	381	422
Сценарий 3 (тренд-прогноз по фактическим данным, D min = 33%, D max = 36%)	344	381

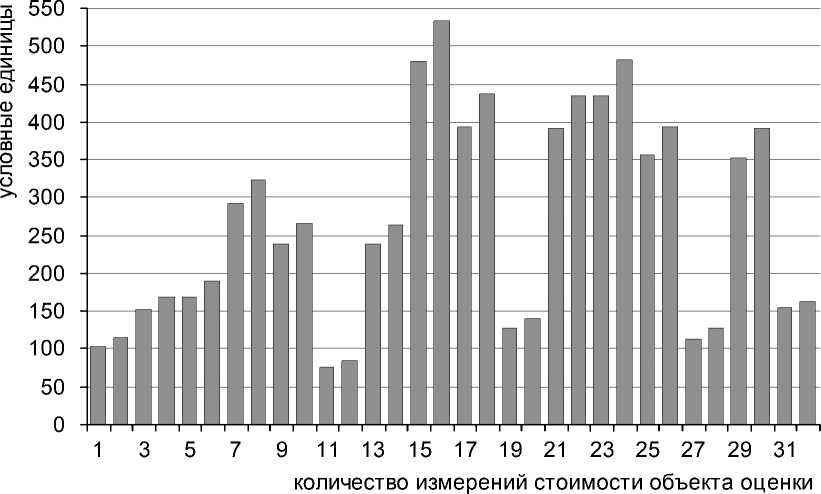
Рис. 3. Результаты измерений стоимости методом ДДП для последующей статистической обработки

Оценка в рамках доходного подхода с использованием комбинации нескольких вариантов (модель 2) показала, что стоимость объекта оценки находится в диапазоне от 232 до 422 условных единиц. Результаты расчетов представлены в таблице 4.

Оценка в рамках доходного подхода с использованием метода «тренд лицензионных платежей» (модель 3) показала, что стоимость объекта оценки находится в диапазоне от 155 до 163 условных единиц, а среднее значение составило 159 условных единиц.

При использовании каждого метода были применены различные сценарии, и в совокупности методом ДДП были рассчитаны 32 значения рыночной стоимости объекта оценки. Не отдавая предпочтение какому-либо методу (сценарию), оценщик принял допущение, что все 32 полученных результата являются достоверными и относятся к статистической выборке результатов измерения (оценивания) одной и той же величины – рыночной стоимости объекта оценки. На этом основании была проведена статистическая обработка полученных результатов и определены среднее значение (268 у. е.), стандартное отклонение (138 у. е.) и доверительный интервал [130; 406]. Значения, полученные в результате статистической обработки, представлены в таблице 5.

В известной монографии Д. Фридмана и Н. Ордуэя согласование результатов оценки стоимости называется «экзаменом совести» и при этом подчеркивается «что согласование – это не процесс механического усреднения результатов» [24]. В определенной степени статистическая обработка результатов дает именно механическое усреднение, но позволяет численно установить границы интервала значений рыночной стоимости объекта оценки. В нашем случае по состоянию на дату оценки расчетное значение рыночной стоимости прав на энергосберегающую технологию составило (268 ± 138) условных единиц.

Метод согласования результатов оценки, основанный на нечеткой логике

Анализ результатов расчетов стоимости, полученных методом ДДП для трех моделей, показал наличие НЕ-фактора «неоднозначность» в связи с тем, что итоговый интервал стоимости для модели 2, то есть [232; 422], не пересекался ни с одним из результирующих

Таблица 5

Статистическая обработка результатов оценки стоимости

Среднее 268,3606 Стандартная ошибка 24,40684 Медиана 251,3885 Мода н/д Стандартное отклонение 138,066 Дисперсия выборки 19 062,21 Эксцесс -1,314566 Асимметричность 0,278638 Интервал 457,3651 Минимум 75,93503 Максимум 533,3001 Сумма 8 587,538 Счет 32 Уровень надежности (95,0%) 49,77811 интервалов стоимости для моделей 1 и 3, которыми оказались, соответственно, интервалы [103; 189] и [155; 163]. Это означает, что при согласовании результатов, полученных для каждой из трех моделей, необходимо дополнительно учитывать информацию о скрытой связи достоверности исходных данных с явно заданными интервалами стоимости, определенными на основе исходных данных. Поскольку нечеткая логика позволяет учесть связи этого типа, она была использована при разработке метода согласования результатов оценки, позволяющего устранить неоднозначность в процессе согласования результатов для моделей 1, 2 и 3, а также в любых аналогичных задачах согласования.

Основными шагами метода являются:

• 1)    приведение к нечеткости (фаззификация) – представление значений стоимости оцениваемого объекта в виде функций принадлежности, определяющих нечеткие множества значений стоимости. Этот шаг выполняется путем обобщения существующих методов расчета стоимости, основанных на статистических методах, или путем обработки экспертных оценок, а также на основе другой информации, доступной на момент оценки стоимости объекта;

• 2)    нечеткое согласование . В зависимости от степени неоднозначности альтернативных результатов оценок стоимости и полноты исходной информации для определения критериев ранжирования альтернатив выполняется согласование результатов либо путем ранжирования, либо с использованием согласующего нечеткого множества, которое, в частности, может формироваться за счет объединения или пересечения нечетких множеств;

• 3)    приведение к четкости (дефаззификация) . На этом шаге получают значение стоимости в виде четкого числа на основе согласующего нечеткого множества.

При использовании рассматриваемого метода согласования в рамках доходного подхода было выполнено обобщение метода ДДП, представленного формулой (1). Как отмечено ранее, в тех случаях когда известна информация о стоимостных ограничениях, вы- раженных в виде интервалов, возможно использование этой информации для построения кусочно-линейных функций принадлежности. Особенности извлечения исходных данных об объекте оценки позволили определить только минимальные, максимальные и наиболее вероятные значения потоков выгод, ставок дисконтирования и капитализированного денежного потока в постпрогнозном периоде, поэтому обобщение метода ДДП было выполнено с использованием только треугольных функций принадлежности. Подробно этот метод рассмотрен далее.

При согласовании оценок рыночной стоимости, полученных методом ДДП, использованы нечеткие числа с треугольной функцией принадлежности . При этом нечеткое число определялось как выпуклое, нормализованное нечеткое множество A с R , чья функция принадлежности по крайней мере кусочно-непрерывна и имеет значение μA (x) = 1 на точно одном элементе. Для определения стоимости, полученной методами ДДП, в виде нечетких чисел было выполнено обобщения формулы (1), в результате которого стоимость стала определяться тройкой чисел ( Vpa , Vpb , Vpc ) со значением в точке x , вычисляющимся согласно выражениям (2):

(Vpa - x)/(Vpb - Vpa), Vpa < x < Vpb pA (x) = j (Vpc - x)/(Vpc - b), Vpb < x < Vpc

0, в остальных случаях n-1

Vpa = £ i=1

CFai

( 1 + Da iF, 5

CFa n + Reva.

\ n — 0 , 5 * ⁺ Da n )

n - 1

Vpb = £ i=1

CFbi

( 1 + Db , ) ' ^{- 0} , 5

CFb n + Revb ; ( 1 + Db n ) n ^{- 0} , 5 ;

n - 1

Vpc = £

= 1

CFc_i ( 1 + De , ) ' ^{- 0} , 5

CFc n + Re vc

О —   \n - 0 , 5

^{+ D}c n )

где Vpa_, Vpb_, Vpc – минимальная, наиболее вероятная и максимальная стоимость объекта оценки;

CFa_i, CFb_i, CFс_{i ,} – минимальный, наиболее вероятный и максимальный потоки выгод (денежный поток) в i -м году;

CFa_n , CFb_n , CFc_n – минимальный, наиболее вероятный и максимальный потоки выгод (денежный поток) в последний прогнозный период;

i – порядковый номер года получения выгод от использования запатентованной технологии;

• n    – количество прогнозных лет (периодов) – определяется экономическим сроком жизни объекта;

Reva , Revab , Revc – минимальное, наиболее вероятное и максимальное значения капитализированного денежного потока в постпрогнозном периоде (если прогнозный период совпадает со сроком экономической жизни объекта, то Reva = 0, Revb = 0, Revc = 0);

Da_i , Db_i , Dс_i – минимальная, наиболее вероятная и максимальная ставки дисконтирования в i -м году (для моделей 1 и 2 в первом прогнозном периоде – 33, 34,5 и 36% соответственно, а для модели 3 – 16% для любого из периода);

Da_n , Db_n , Dc_n – минимальная, наиболее вероятная и максимальная ставки дисконтирования в последний прогнозный период (для моделей 1 и 2 – 28,12; 28,97 и 29,82% соответственно, а для модели 3 – 16%).

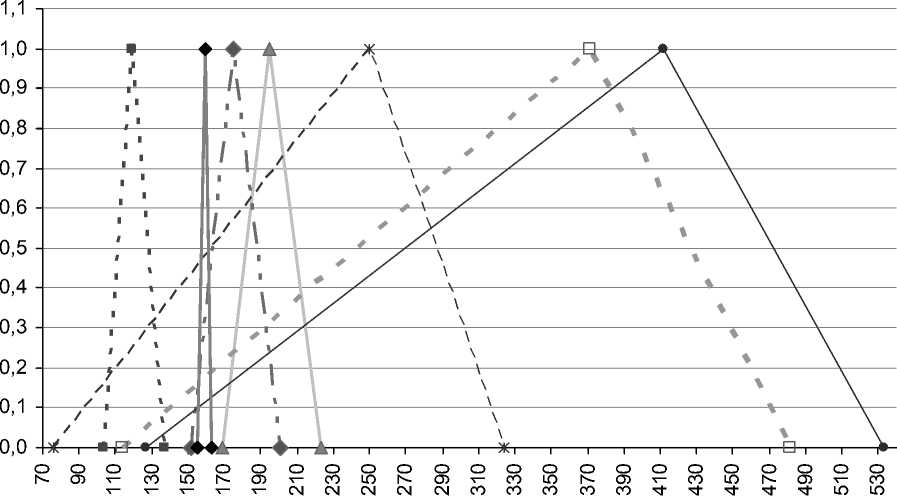
С помощью обобщенного метода, представленного формулами (2), для каждой из трех моделей стоимости объекта оценки были определены расчетные значения рыночной стоимости методом ДДП в виде треугольных функций принадлежности. Тройки чисел ( Vpa , Vpb , Vpc ), определяющих функции принадлежности для каждого сценария каждой модели, представлена в таблице 6. Графически полученные функции принадлежности представлены на рисунке 4.

Таблица 6

Значения стоимости, задающие функции принадлежности

Номер модели	Описание параметров модели в различных сценариях	Значения стоимости, определяющие треугольные функции принадлежности, у. е.
		Vpa	Vpb	Vpc
1	Сценарий 1 (захват рынка – 0,19%, ежегодный рост доли – +15%, выделение эффекта – 25%, D min = 33%, D max = 36%)	103	119	137
	Сценарий 2 (захват рынка – 0,30%, ежегодный рост доли – +16%, выделение эффекта – 25%, D min = 33%, D max = 36%)	169	195	223
	Сценарий 3 (тренд-прогноз по фактическим данным, выделение эффекта – 25%, Dmin = 33%, D = 36%) max	152	175	201
2	Сценарий 1 (захват рынка – 0,19%, ежегодный рост доли – +15%, Dmin = 33%, Dmax = 36%)	76	250	324
	Сценарий 2 (захват рынка – 0,30%, ежегодный рост доли – +16%, Dmin = 33%, Dmax = 36%)	127	412	533
	Сценарий 3 (тренд-прогноз по фактическим данным, D min = 33%, D max = 36%)	114	372	481
3	Ставка дисконтирования D = 16%	155	159	163

Как видно из таблицы 6 и рисунка 4, для модели 1 имеет место неоднозначность, поскольку нечеткое множество, определяющее результат для сценария 1, не пересекается с нечеткими множествами сценариев 2 и 3, что связано с отсутствием пересечений соответствующих интервалов [ Vpa , Vpc ]. Аналогичная неоднозначность присутствует, если сравнивать сценарий 1 модели 1 и модель 2. Однако в совокупности полученные нечеткие множества пересекаются, не оставляя в интервале между значениями стоимости 76 и 533 неучтенных промежутков, что соответствует качественно выполненной оценке, полноценно учитывающей доступные на момент оценки исходные данные.

Полученные решения могут рассматриваться как набор из семи альтернатив, среди которых следует выбрать наиболее предпочтительную, используя, например, слияние нечетких целей и ограничений [7], аддитивную свертку или другие методы ранжирования, рассмотренные, в частности, в работе [8]. Особенностью (допущением) рассматриваемых моделей оценки стоимости является отсутствие достаточной информации для формирования критериев, позволяющих отдать предпочтение одному из семи полученных результатов, что связано с большой неопределенностью параметров стоимостных моделей, из-

рыночная стоимость, у. е.

модель 1, сценарий 1          модель 1, сценарий 2         модель 1, сценарий 3

модель 2, сценарий 1          модель 2, сценарий 2         модель 2, сценарий 3

модель 3

Рис. 4. Треугольные функции принадлежности для трех моделей оценки стоимости меняющихся во времени. Тем не менее такие результаты оценки могут быть согласованы путем построения объединяющего нечеткого множества. Соответствующая согласующая кусочно-линейная функция принадлежности MS(x) определяется следующим множеством точек: (0,000; 76), (0,174; 106), (1,000; 119), (0,317; 131), (0,465; 157) , (1,000; 159) , (0,490; 161), (0,504; 164), (1,000; 175), (0,624; 185), (1,000; 195), (0,726; 202), (1,000; 250), (0,633; 277), (1,000; 372), (0,899; 383), (1,000; 412), (0,000; 533). Графически согласующая функция представлена на рисунке 5.

В процессе дефаззификации на основе согласующей функции принадлежности M_S ( x ) для получения итогового значения рыночной стоимости объекта оценки, в качестве которого принимается «центр тяжести» P_S , использован центроидный метод:

P = J xM s ( x ) dx S J M s ( x ) dx "

В результате расчета по формуле (3) было получено итоговое значение рыночной стоимости объекта оценки методом ДДП – 315 условных единиц. Это значение превышает результат, полученный статистическим методом согласования, приблизительно на 18 процентов, что объясняется тем, что значения, полученные для модели 2, в особенности для сценариев 2 и 3, связаны с наибольшими показателями рыночной стоимости и являются в меньшей степени взаимно неоднозначными, чем остальные согласуемые результаты. Также они компенсируют неоднозначность, возникающую из-за остальных согласуемых значений рыночной стоимости, полученной методом ДДП.

Таким образом, в работе показана перспективность методов, учитывающих НЕ-факторы, для оценивания рыночной стоимости различных объектов.

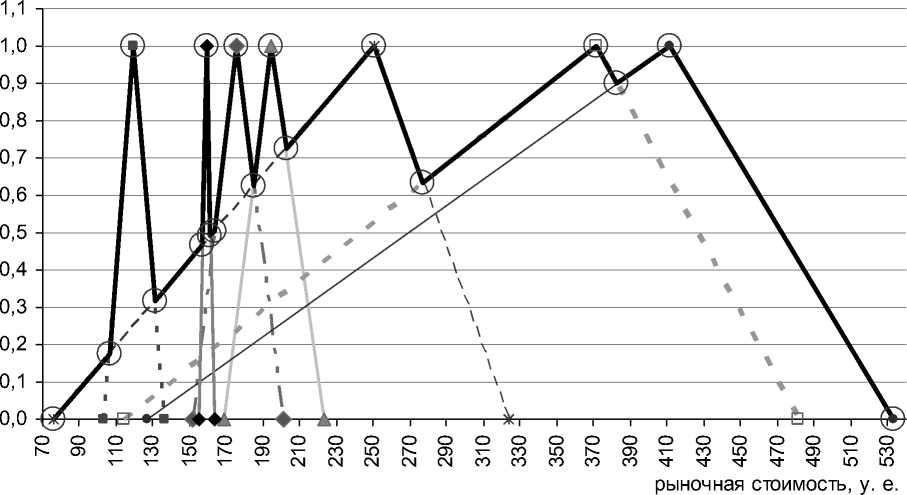
■ ■■ ■ ■ модель 1, сценарий 1     ▲   модель 1, сценарий 2  —♦■ - модель 1, сценарий 3

модель 2, сценарий 1  —•   модель 2, сценарий 2  - в - модель 2, сценарий 3

♦  модель 3           ^^  объединение

Рис. 5. Согласующая кусочно-линейная функция принадлежности