Метод суммарной аппроксимации для многомерного псевдопараболического уравнения третьего порядка

DOI:

Краевые задачи для псевдопараболических уравнений и более общего класса уравнений — уравнений Соболевского типа — возникают при изучении фильтрации жидкости в трещиновато-пористых средах [1; 5], движений почвенной влаги [8; 16; 20], а также при описании тепломассопереноса [6; 7; 12; 13; 19], волновых процессов и во многих других областях.

Широкий спектр результатов по исследованию начальных и начально-краевых задач для сильно нелинейных уравнений псевдопараболического типа, а также вопросов локальной разрешимости, условий разрушения решений и глобальной во времени разрешимости был получен в [10].

Краевые задачи для различных классов уравнений третьего порядка изучались в работах [4; 17; 18]. Разностным методам решения краевых задач для псевдопараболиче-ских уравнений третьего порядка посвящены работы [2; 3; 11]. Краевые задачи с общим нелокальным условием А.А. Самарского для псевдопараболических уравнений высокого порядка изучены в работе [15].

Данная работа посвящена рассмотрению локально-одномерной схемы (ЛОС) для псевдопараболического уравнения в р -мерном параллелепипеде. В предположении существования регулярного решения рассматриваемой задачи получена априорная оценка в дифференциальной форме, откуда следует единственность и устойчивость решения по правой части и начальным данным. Получена априорная оценка в разностной форме для решения локально-одномерной разностной схемы. Доказаны устойчивость и сходимость локально-одномерной разностной схемы. Проведены численные расчеты тестовых примеров, иллюстрирующие полученные в данной работе теоретические выкладки.

1. Постановка задачи

В цилиндре Q _T = G х (0 < t <  Т ], основанием которого служит р -мерный прямоугольный параллелепипед G = { х = (х 1 ,х ₂ , ...,х _р ) : 0 <  х _а < /_а , а = 1, 2, ...,р } с границей Г , G = G + Г , рассматривается задача

= Lu + р ^-Lu + /(x,t), (x,t) G Q t , (1) at at

и

= 0,  0 <  t <  Т,

г

и(х, 0) = и ₀ (х),  G = G + Г,

р где Lu = V Lau; Lau = а=1

9 ди

I к_а ^{( х)})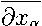

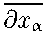
; 0 < с ₀ <  к_а (х) <  с 1 ; и = const > 0 ; с о , с 1 —

положительные постоянные; Q _T = G х (0 < t <  Т ] ; а = 1,р .

Как отмечено в работе [16], второе слагаемое в правой части уравнения (1) очень

мало при впитывании и велико при испарении.

Далее предполагается, что решение дифференциальной задачи (1)–(3) существует и обладает нужными по ходу изложения производными. Относительно коэффициентов задачи (1)–(3) предположим, что они обладают таким количеством непрерывных производных, которое необходимо для обеспечения нужной гладкости решения и(х, -) в цилиндре Q _T .

2. Априорная оценка в дифференциальной форме

Предполаг ая существование регулярного решения дифференциальной задачи (1)– (3) в цилиндре Q _T , методом энергетических неравенств получим априорную оценку для ее решения. Для этого умножим уравнение (1) скалярно на и и преобразуем полученное тождество:

(dt^) = (^Lu,u) ⁺ (и llt^Lu,U) ⁺ (^ ^{( х,t ) ,u})^, где скалярное произведение и норма вводятся следующим образом:

Г                                       Р

(^и,с) = ии.^х, ^(и,и) = И ^и ^ о , ^и х = 52

а=1

G

^и 1 с а ,    Н ^и Н ь 2 <0,/ а ) =

Z а

У u²(х,t)dх_a. о

Преобразуем интегралы, входящие в тождество (4), с учетом (2):

(|U,u) = / ^ = 2 д Л<

G

И = (² м (^{М х )} ii^ ) -^u ) = /t м„ (^ ^{( х )} м ) ^и*^х= а 1                                      g^ а1

= Е / ^Т; (^ <^х> di ; ) ^и*^х = ^- Е / X ^{( х}) (д| - ) *^х, а — 1 G                             а — 1 G

( ^ dl^Lu,^u ) = ( ^ 52 hix r. ( * « ^{( х )} д£ ) -^и ) = ^ц /^2 д1а1 а ( ^ - ^{( х )} дх ; ) ^и^^х = а=1                                g а=1

И- 9          , и(8и

= ^- 2 g-Mj М^х> (ах;)*¹.                   ¹

^; =1 G

Для оценки последнего слагаемого в правой части (4) применим неравенство Коши

(/ (X/t),!^ = У

G

1                    1

/ (X,tw <  2 ' / ' 0 + 2 м2 .

Подставляя (5)–(8) в тождество (4), получаем

1 d h d А Г , , J ди V , Ar, , d du V ,   1      1

2at'Mo + 2at t ka(x\mJ dx + АAaX") dx < 2”u”o + 2'”«• a1 G                       a1 G

Откуда следует неравенство dt ^'2 +

d dt

t / Mx) (   ) 2 ^dx + f / , . ( x ) (   )

a—1 G                      a—1 G

dx < M 1 ' u ' 2 + M ₂ ' / ' 2 , (9)

где M 1 , M 2 зависят только от входных данных задачи (1)-(3).

Проинтегрируем (9) по т от 0 до t, тогда получим llullo + IA IL + IAIl2,Qt < M3

/‘ ' и ' 0

2 dT + M 4

( У Н У 112 ^{d T +} I ^u o ( ^X ) 1 и ₂ ( G,) ,

где M3, M4 зависят только от входных данных задачи (1)-(3). Применяя лемму Грону-олла [9] к (10), находим неравенство у |u|2dT

где M5 зависит только от входных данных задачи (1)-(3). Учитывая (11), из (10) получаем априорную оценку

^|u|Wi(G) ^{+ |u}^'2,Q_t<^M(t)(y ^^{12dT + |u}0^(x)l2K2i(G)),            ⁽¹²⁾

где M(t) зависит только от входных данных задачи (1)-(3).

Из априорной оценки (12) следует единственность решения исходной задачи (1)– (3), а также непрерывная зависимость решения задачи от входных данных на каждом временном слое в норме пространства Ж₂1 (G).

3. Построение локально-одномерной разностной схемы

Пространственную сетку выберем равномерной по каждому направлению Ox_a с шагом h_a, h_a = t_a/N_a, a = 1, 2, ...,p. Совокупность ш^ точек (х1^г1),х(>^г2),..., xO^), •••, Xp^p)) пересечения этих плоскостей назовем узлами разностной сетки.

р шК        шНа,      шНа    {xa      iaha,   ^a 0, 1, •••, ^а,   ^aha    Гх,   a    1, 2, •••,p}.

α=1

Множество узлов, принадлежащих границе Г, назовем граничными узлами, yk =

= (x^ E Г), где Y

_а— левый граничный узел х_а = 0, а y_+- — правый граничный узел

^xа    ^а-

На отрезке [0,T] введем равномерную сетку ш_т = {t₃= jт, j = 0,1,

-,jo} с

шагом т = T/j_a. Каждый из отрезков [t₃, t₃₊₁] разобьем на р частей точками tj+а = t₃+

+ т-, а = 1, 2, ...,р — 1 и обозначим через А_а полуинтервал (t ■, а-1, t₃₊а], а = 1, 2, ...,р.

Р                                                                        ³+р-,    р^

Уравнение (1) перепишем в виде

^и =    — Lu — p-^-Lu — / (x, t) = 0, dt              dt v , ’

или

vP                  1 du           d

^-u = 0, K-u = -   — L-u — P-t^Lu- а=1                 р dt           dt

-

/а,

Р где /а(х,р — произвольные функции, удовлетворяющие условию нормировки ^ / а = /.

а=1

На каждом полуинтервале А_а, а = 1, 2, ...,р, будем последовательно решать задачи

V(-) = " ⁹^(7¹ р dt

-

L-d(-)

-

pl-Ld- — /а = 0, x EG, t E Аа, а =1, 2,...,р,   (13)

dt

^(а) = 0, полагая при этом (см.: [14, с. 522])

^x- ^{E Г}а,

^(1)(х, 0)=Ua(x), ^(_a)(x,t_j+ а-1) = ^(а-1)(x,tз ₊а-1), а =2, 3, ...,р, j = 0, 1,

...^,ja

— 1,

d(1)(x,t3) =^(p)(x,tj), j = 1, 2,...,ja, и Га — множество граничных точек по направлению ха.

Аппроксимируя каждое уравнение (13) с номером а на полуинтервале tj₊«-1< < t < tj₊а двухслойной неявной схемой с весами, получим цепочку р-одномерных схем (ЛОС):

У3 + р

-

3+— у ^р

τ

= Ла^аУ³^ + (1

-

^а)у^{3+ р} ) + рЛ-У^ ^Р + Ф-^{+ Р}

,

где

Л-У^3+р= (а_ау³а^р ) ;   О- = kа(x⁽ 0’^5а));

Жа

_х(-0,5а)

Будем считать σ_α

= (xi, ...,X--1, Xа

— 0, 5^_а, x_-+1,..., x_P), p = const > 0.

= -. Тогда получим У-а = ^Ла(^{0, 5}^У

У3 ⁺Р

= 0,

^Yh, а

+а     3+а-1\      3+а\     3 + а р + У р ) + РУ-ар) + Фа р ,	(14)
j = 0, l,-,ja, а= 1,2,...,р,	(15)
у(x, 0) = ua(x),	(16)

у3 + E где У-t а = -----

-

3+^а ' у р

τ

р

.

4. Погрешность аппроксимации

Пусть и = и(х^) — решение задачи (1)-(3), а у*^{+ р}, а = 1,2,

..

.,р — решение

задачи (14)-(16). Характеристикой точности ЛОС является разность z*⁺¹= у*⁺¹

-

u*⁺¹.

Промежуточные значения у* ⁺р будем сравнивать с и*⁺р = u(x,tj₊a), полагая z^j+р =

= у*⁺р

-

и*⁺р

.

Подставляя у* ⁺р грешности Z(_a) = z*^+р

= z*⁺р + и*⁺р в разностную схему (14)-(16), получим для по-задачу

или

z3+ р

-

τ

*+ ^—1

=Л.(о, 5(z* + р + z*+-- ) + ^zt+ Р ) +

+ Л_а (°, 5 (и*^{+ р}

+ ^и* ⁺   ) + Ц^и^^р )

и*⁺р

-

-

τ

*+ ^-1

-+ ф* ^{+ р},

z^ р

= 0, z(x, 0) = 0, ^Y^, а

^zt„ = ^Ла (⁰, ⁵(^z(a) + ^Z(a-1/) + ^^zt_а ^ + ^Фа ^р, Z(a) = 0, X G Yh,a, z(x, 0) = 0, Z(a) = z*^{+ р},

^Фа ^р=^Ла(^{0, 5}(^и(а) + ^и(а-1)) + ^^и4_а+ ^ф(а) - ^t^.

Вводя обозначение

Р °

1 ди *^+1/2

^фа = I La^u + ^La^ut + /а ^—рд^ )

Р

и замечая, что Е Ф_а = 0, если ^ f _а= f , представим погрешность ф'

а=1

*+

Фа ^р = °а + ^а, где

а=1

*+-

।_а^р в виде суммы

Ф*а = (0, 5Ла(и_М

-

(U(a-l)) - (^и)  2 +

°

*+-

+ (фа ^р

-

°

то есть фа = Фа + Ф£, Фа

/2 ⁾- ^ ^и(а) ^{- и}(а-1) Р °

(^Лаи_а— ^Laut ⁺ 2) +

1 / ди -\3 ⁺ 2 ⁾

- р dt      ¹

Итак, имеем цепочку

= о(1), £^а = о, фа

о(^а+^т).

а=1

одномерных схем при каждом а = 1, 2,

..

.,р. Каждое урав-

нение (14) номера α в отдельности не аппроксимирует уравнение (1), но аппроксимирует уравнение К_а^(_а) = 0 в обычном смысле, и сумма погрешностей аппроксимации ■ф = ф1 + Ф2 + ... + фр стремится к нулю при т ^ 0 и |^| ^ 0. Поэтому система разностных уравнений (14) является аддитивной схемой. Итак, для погрешности z = у — и имеем задачу

^zt _а = ^Ла (° ⁵ (^z(a) + ^Z(a-1/) + ^^zt _а ^ + Фа ^р,

z

= 0,   z(x, 0) = 0.

^Y^, а

5.    Априорная оценка в разностной форме Умножая уравнение (14) скалярно на 0, 5 (U(a) + U(a-1)) + WUta, получим

⁰, ⁵ (^yta , ^U(a) + ^U(a-1)) _а + ^WH^Uta II Ь2(а) ^—

— (Ла (° 5(у(а) + у(а-1)) + WIH^ , 0, 5(у(а) + у(а-1)) + WUta^ =

= (V+ Р , 0, 5 (^У(а) + U(a-1)) + WUta) ,                       (19)

где

(^V,V) = E ^nvН, жЕш_к

Н = П ha, а=1

Na-1            /          Na

{^М,У) = 52 ^M«a ^Via ^ha, (U,y| = ^Via Via^ha. ia = 1                             ia=1

Преобразуем слагаемые, входящие в (19), с учетом граничных условий и разностного аналога теоремы вложения (см.: [14, с. 120]). Получим:

^{0 5}^U(a) ^-U(a-1)^,U(a) + U(a-1))_а+ W^Uta ^|2т+ (^oa^,(^{0, 5}^U(a) ^-U(a-1)) + WUta) _ ) _a^T<

< 4; ll^^+РIIW + - 8

T, Л2(а)

(0 ⁵ (U(a) + U(a-1)) + WUta) xx         /      / Ж a

или

^{0 5|}U^J+P^t(a) + W^Uia HL(a)^T+ (^Со

-

12 - 8

)  (^{0, 5}(U(a) ^-U(a-1)) + WUt

It

О

' ж a

τ≤

Л2(а)

< 4; Цф^^+Р^L(a)^T+ ^{0, 5|}U^{J+ -pV} ^L(a)

После суммирования (20) по tg = Ч, в = 1, 2,

, Zq = max 1а.

ОС

Со

..

.,Р при Е =  2 получим

^4-о

^{0, 5|}U^J+aНь₂(_Шк) + WHUta л^г. ^т+ у

(0 ⁵(Ua) ^-U(a-1)) + WUta)

XX        /      / Ж a

Ь2(ш_к)

τ

≤

< -°ll^^+p HU_h)T + 0^, 5|U^⁺-- ||^_h).

^c0

Суммируем (21) сначала по a = 1, 2, ...,p

Р

^{0 5 |}U^{j + 1|}L2(w_h) + V ^ llUta IlL (W.)^T а=1

+ "2" ^  ^⁰>⁵^a) ^{— U}(a-1)) + ^WUt,

р

а=1

■)

Ж a Ь2(ш_к)

τ≤

7 2 Р

< -⁰E k^3+pii,<.₁)T+0,sbu^Bi₁₍„.),

^Соa=1

а затем по j‘ от 0 до j

' Р

^|y^,41|L₂(Wh) ⁺ ^ Е ^тЕ IW^h) ⁺

'‘=0 а=1

3 Р

^+с° Е^тЕ I^0,5С '‘=0 а=1

1/^+р + ,/' ^р ) + р,^ ^{+ р} )

≤

Ха L2(w_h)

< ²ЕтЕи^^+р12 (.,„ + HMx)^.^.

^С0'‘=0  а=1

Итак, справедливо следующее утверждение.

Теорема 1. Локально-одномерная схема (14)–(16) устойчива по начальным данным и правой части, так что для решения задачи (14)–(16) справедлива оценка (22).

6.    Сходимость локально-одномерной схемы

Решение задачи для погрешности Z(_a) = z^ р будем искать в виде суммы Z(_a) = = ^(_а) + П(_а), где П(_а) определяется условиями (см.: [14, с. 528]):

П(а)

-

τ

п(а-1)

------= -а, X G ^hа + Ya, а = 1, 2, ...,р,

п(х, 0) = 0.

Отсюда находим n'⁺¹= П(_Р) = П³+ т^—1 + —₂+ ... + ф_р) = п' = ... = П⁰= 0, для j = 0,1,...,j₀, так как п(ж, 0) = 0. Для п(_а) имеем П(_а) = т^—1 + —₂+ ... + ф_а) =

т(ф_а+1 + ... + фр) = О(т).

-

Функция и(_а) определяется условиями:

Via = Ла (0, 5 ^(а) + V(a-1)) + ^^ta) + - а, X G W_h, а = 1, 2, ...,р,

- а = -а + Ла(^П(а) + П(«-1)) + Р-Л_аП_а.

—              d ⁴и

Если существуют непрерывные в замкнутой области Q_T производные ₉ , а = 0x00x1

= в, то Л_ап(_а) = -тЛ_а(ф_а+1+... + ф_р) = О(т), так как П(_а) определяется из уравнения (23). Будем считать, что ц = ^(т) стремится к нулю как и т (то есть ц = О(т), ц G G (0,т]), тогда г-а = 0(^1 + т).

Решение задачи (24) оценим с помощью теоремы 1.

Так как п' = 0, П(_а) = О(т), то Iz'|| < ||г?||, тогда из оценки (22) следует утверждение.

Теорема 2. Пусть задача (1)-(3) имеет единственное непрерывное в QT решение u(x,t) и существуют непрерывные QT производные д 2и     д 4и      д 3и дt2, дх2адхв, dx2adt1

д2 / дх2,   а = 1,2,...,р,   а = 3, тогда локально-одномерная схема (14)-(16) сходится со скоростью O(|h|2 + т), так что ц^+1 - и^ <М ^|2 + т), |h|2 = h2 + h2 + ... + h2, j = 1, 2,..., где М = const > 0 не зависит от т и ha; р = О(т), р G (0, т];

j р ll^ 11l = II^IIm^) +2^ E т E ll^a llL(wh) + j'=0  a=1

j р

+=0 E т E j '=0  a=1

(0, 5(y^j'^+a

+ ^У '^{+ a-1} ) + ^^ ^P )  ]

' ZaJ

12(mh)

Замечание 1. Полученные в данной работе результаты справедливы и в случае, когда

T 8          ди\

- д_а(х,к)и(х,€),

L_au =      k_a(x,t)

дха        дха / если 1ка1(х,€),да(х,к)1 < =2.

7.    Результаты численного эксперимента

Коэффициенты уравнения и граничных условий задачи (1)-(3) подбираются таким образом, чтобы точным решением задачи была функция u(x₁,x₂,t) = е*(х1 — /1х²)(х3 — ^—^2^х2) •

Ниже в таблицах 1–3 при уменьшении размера сетки приводятся изменения максимального значения погрешности (z = у — и) и порядка сходимости ПС) в нормах |[-]|о и II • Нс(wt), где 1у1с(^т) = , ^та^х |у|, когда h = Vr ^ = 0,1 т, ^ = т, ^ =10т. (Xi,tj )Gw_hT

Погрешность уменьшается в соответствии с порядком аппроксимации O(|h|²+ т). Порядок сходимости определяется по следующей формуле: ПС= log^1   11k, где _2j— это

^2 ^|[z2^]|0

погрешность, соответствующая hi.

Заключение

Настоящая работа посвящена изучению первой начально-краевой задачи для псев-допараболического уравнения третьего порядка в р-мерном параллелепипеде. В предположении существования регулярного решения рассматриваемой задачи получена априорная оценка решения в дифференциальной форме, откуда следует единственность и устойчивость решения по правой части и начальным данным. Построена локальноодномерная разностная схема и для ее решения получена априорная оценка в разностной форме. Доказаны устойчивость и сходимость локально-одномерной разностной схемы. Проведены численные расчеты на тестовых примерах, иллюстрирующие полученные в данной работе теоретические выкладки.

Таблица 1

ц = 0.1т	h = VT	max l[zj]|o 0<3	ПСв |[.]|o	Нг11с(шкт)	ПСв II • llc^)
0,00025	1/20	0,057710797		0,189397602
0,0000625	1/40	0,016911749	1,7708	0,060197781	1,6536
0,0000156	1/80	0,004498392	1,9105	0,016556651	1,8623
0,0000039	1/160	0,001152122	1,9651	0,004296175	1,9463
0,0000009	1/320	0,000290934	1,9855	0,001091661	1,9765

Таблица 2

µ=τ	h = VT	max |[^]|o 0<3	ПСв IHlo	IHIc (w^t)	ПСв II • Ic(^.T)
0,0025	1/20	0,039455664		0,118419311
0,000625	1/40	0,015632359	1,3357	0,054218784	1,1270
0,000156	1/80	0,004821030	1,6971	0,018377096	1,5609
0,000039	1/160	0,001307758	1,8822	0,005188275	1,8246
0,000009	1/320	0,000336338	1,9591	0,001350971	1,9413

Таблица 3

µ= 10τ	h = л/т	max l[z3]|o 0<3	ПСв l['llo	h^hc (шнт)	ПСв II • llc(wht)
0,025	1/20	0,184385227		0,499145325
0,00625	1/40	0,131402676	0,4887	0,387724356	0,3644
0,00156	1/80	0,062711258	1,0672	0,205996093	0,9124
0,00039	1/160	0,021631656	1,5356	0,078851858	1,3854
0,00009	1/320	0,006199708	1,8029	0,023959349	1,7186