Методические особенности обучения методам математического анализа студентов педвуза в условиях бакалавриата

Общеизвестно, что чем больше методов освоил человек,тем большее количество разнообразных задач он может решить. В современной энциклопедической литературе метод (от греч. methodos – путь исследования, теория, учение) трактуется как способ достижения цели, решения конкретной задачи; совокупность приемов и операций практического или теоретического освоения (познания) действительности [Большой энциклопедический словарь 1998: 452; Всемирная энциклопедия 2001: 634].

Основатель аналитической геометрии, автор научного трактата «Рассуждение о методе, позволяющем направлять разум и отыскивать истину в науках» (1637 г.) Р. Декарт в другой своей работе «Правила для руководства ума» так раскрывает сущность метода: «Метод состоит в размещении и упорядочении того, на что должно быть направлено остриё ума в целях открытия какой-либо истины» (Правило V) [Декарт 1936].

В современной дидактике общепризнанным является то, что «всякий метод является системой осознанных последовательных действий человека, приводящих к достижению результата, соответствующего намеченной цели» [Дидактика средней школы 1982: 186]. Высказываются также суждения, что понятие способа не является родовым, то есть более общим по отношению к понятию метода. У понятия метода – два родовых понятия. Для субъективной стороны метода родовым служит понятие способа. Метод – это такой способ деятельности, который основан на познанной (относительно конечно) сущности предмета деятельности. Есть способы, основанные на чисто эмпирическом опыте. По отношению к объективной стороне метода родовым является понятие системы знания: «Знание объективных закономерностей, на которых основан метод, организовано в виде некоторой системы. Без системы знаний не может существовать метода. <…> Ни одна система знания полностью не реализуется в методе, она по своему содержанию богаче его, не сразу система становится методом» [Логика научного исследования 1965: 306]. «Метод – это такая система знаний, которая уже используется или для дальнейшего познания, или для преобразования объекта. Знание в процессе обучения переходит в метод. Одинаково ошибочны отождествление метода со способом деятельности или, напротив, отрыв сущности метода от способа и формы его реализации» [Шапоринский 1981: 155–156].

Известный педагог В. И. Андреев считал, что некорректно определять «метод» через понятие «способ», так как это слова одного синонимического ряда. «Способ не может быть родовым признаком по отношению к категории «метод», – отмечает В. И. Андреев, – таковым признаком является деятельность. Метод характеризует деятельность с позиции процесса, поэтому метод – процессуальная характеристика деятельности. Но не любой процесс есть метод. Метод выступает нормативной моделью процесса деятельности, определяя, как нужно действовать наиболее рациональным и оптимальным образом в процессе решения соответствующих задач» [см.: Шиянов, Котова 2000: 240].

На практике необходимым условием правильного применения метода является определенная система знаний, без которых метод не существует. Такая система должна содержать: 1) исходные знания об объекте, к которому применяется метод, его свойствах; 2) знания, полученные в ходе преобразования или изучения объекта; 3) знания о сфере приложения метода (круг задач, решаемых с помощью данного метода, их виды и т. д.); 4) знания об особенностях его использования в зависимости от сферы приложения.

К деятельностным компонентам метода относятся: 1) определенная система действий, реализация которой ведет к достижению результата, соответствующего намеченной цели; 2) средства осуществления деятельности, основу которой составляет эта система действий.

Таким образом, для того чтобы освоить какой-либо метод, необходимо овладеть соответствующей системой знаний и системой действий.

В педагогическом вузе одной из фундаментальных математических дисциплин является математический анализ. Качественное усвоение содержания этой дисциплины важно не только для дальнейшего обучения и формирования научного мировоззрения будущих педагогов, но и для их будущей профессиональной деятельности. Начала математического анализа изучаются в школе и цель его изучения не в том, чтобы выработать у школьников навыки дифференцирования и интегрирования, а в том, чтобы создать возможность для расширения области приложений школьной математики. Последнее достигается посредством решения задач. В качестве методов в этом случае выступают методы дифференциального и интегрального исчисления. К первым относятся методы исследования функций на монотонность, экстремум, наименьшее и наибольшее значения, выпуклость и точки перегиба. К методам интегрального исчисления относятся методы нахождения площадей, объемов, длин дуг и других величин с помощью определенного интеграла.

В школьных учебниках алгебры и начал математического анализа, а также геометрии имеются специальные разделы, в которых рассматриваются случаи применения интеграла к решению геометрических задач на вычисление площадей и объемов фигур. Поэтому одна из задач учителя – познакомить учащихся с перечисленными методами и научить правильно применять их при решении задач.

К сожалению, в условиях бакалавриата количество часов на фундаментальные математические дисциплины сократилось – некоторые разделы изучаются в рамках дисциплин по выбору. В частности, нами разработано содержание дисциплины «Геометрические и физические приложения определенного интеграла», позволяющее более глубоко изучить этот раздел, рассмотреть методы решения задач разных типов и видов. Для студентов подготовлено специальное учебное пособие, позволяющее систематизировать все полученные в этой области знания и формировать соответствующие умения. Например, методы вычисления площадей фигур делятся на три вида в зависимости от того, каким образом задана кривая: в декартовых координатах, в полярных координатах или параметрически.

Рассмотрим подробно методы решения задач на вычисление площадей, когда кривая задана в декартовых координатах. Деятельностный состав этих методов представлен на Рис. 1. Опишем особенности их применения.

• I.    Метод непосредственного применения формулы для вычисления площади криволинейной трапеции

S=S b f(x)dx           (1)

Здесь необходимо показать студентам, что этот метод непосредственно применяется в двух случаях:

• 1)    когда задана функция f(x) и пределы интегрирования;

• 2)    когда функция f(x) задана, а пределы интегрирования надо найти из условия задачи. Приведем пример.

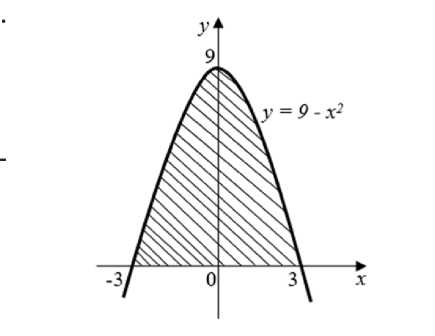
П р и м е р 1. Вычислить площадь фигуры, ограниченной параболой y= 9 - x² и осью абсцисс.

Для решения задачи необходимо выполнить три действия:

• 1)    построить фигуру по данным задачи (Рис. 2);

• 2)    найти пределы интегрирования (в данном случае найти точки пересечения параболы с осью абсцисс), то есть решить уравнение 9 - x² = 0 ;

Рис. 1. Деятельностный состав методов вычисления площадей фигур в декартовых координатах

• 3)    вычислить площадь фигуры, применяя формулу (1)

• II.    Метод, основанный на свойстве аддитивности площади.

Данный метод применяется в случае, когда заданы две функции, графики которых имеют точки пересе чения. В этом случае полученную фигуру приходится разбивать на части. Приведем пример.

П р и м е р 2. Найти площадь фигуры, ограниченной графиками функций y= 2 x², y=x²+ 1 , x = -2, x = 3.

Для решения задачи необходимо выполнить четыре Рис. 2. Фигура к примеру 1. действия:

• 1)    построить фигуру по данным задачи (Рис. 3) и установить, является ли она криволинейной трапецией; если не является, то ответить на вопрос: почему (ответ обосновать), и как в этом случае вычислить её площадь;

• 2)    разбить фигуру на части (в данном случае фигура состоит из двух криволинейных трапеций);

  

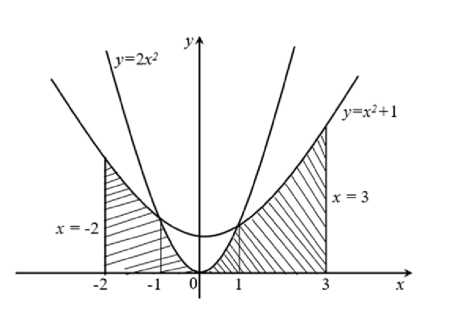
  Рис. 3. Фигура к примеру 2.

  
  

  3) найти пределы интегрирования, для этого найти абсциссы точек пересечения построенных графиков из уравнения x²+ 1 = 2 x² , откуда x = ±1 ;

  4) вычислить площадь фигуры как сумму площадей четырех составляющих её криволинейных трапеций.

  

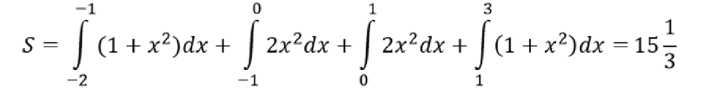
  2x²dx +

  2x²dx + I (1 + x²)dx

  
  

III. Метод, основанный на разности площадей двух криволинейных трапеций, ограниченных графиками функций f₁(x) и f₂(x) (Рис. 4).

Площадь фигуры в этом случае вычисляется по формуле

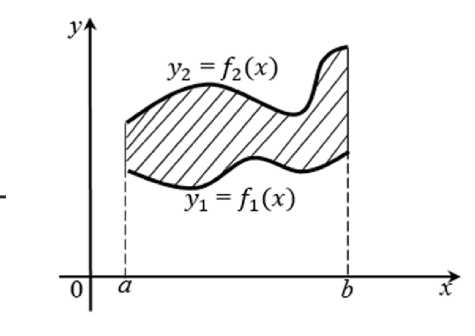
yi = №)

У2 =/2 to

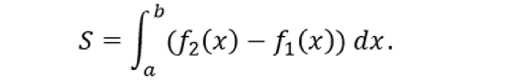
П р и м е р 3. Найти площадь фигуры, ограниченной графиками функций y=^x и y=x²

Для решения необходимо выполнить следующие действия:

• 1)    построить фигуру по данным задачи (Рис. 5) и установить, является ли она криволинейной трапецией; если не является, то ответить на вопрос: почему (ответ обосновать), и как в этом случае вычислить её площадь;

• 2)    найти пределы интегрирования, т. е. решить уравнение

x2=√x,откуда x1=0, x2=1;

• 3)    определить, какой из графиков расположен выше, а какой ниже;

  о                       1

  Рис. 5. Фигура к примеру 3.

  
  

• 4)    вычислить площадь фигуры как разность площадей двух криволинейных трапеций, применяя формулу (2):

s =

• IV.    Метод вычисления площади фигуры, когда функция f(x) на отрезке [a,b] удовлетворяет условию f(x)≤0.

В этом случае для вычисления площади фигуры используется её симметрия относительно оси , либо специальная формула

S = - Jb, f(x)dx

Если некоторые части кривой y=f(x) расположены выше оси Ox, а другие – ниже оси Ox, то площадь всей фигуры представляет собой алгебраическую сумму площадей тех частей фигуры, которые расположены над осью Ox и тех её частей, которые находятся под осью Ox, причем первые входят в сумму со знаком плюс, а вторые – со знаком минус. Поэтому площадь фигуры в данном случае можно выразить формулой

S = Jb, \f(x)\dx

• V.    Комбинированный метод – это метод вычисления площади фигуры, предполагающий сочетание всех предыдущих методов и включающий поэтому действия, входящие в их состав (см. схему на рис. 1). Приведем пример.

П р и м е р 4. Вычислить площадь фигуры, ограниченной графиками функций y=x3,y=(x-2)2,x=-1 и осью абсцисс.

Для решения задачи необходимо выполнить следующие действия:

• 1)    построить фигуру по данным задачи (Рис. 6);

• 2)    разбить фигуру на части (часть фигуры, которая находится над осью Ox, состоит из двух криволинейных трапеций);

• 3)    найти пределы интегрирования, т. е. решить уравнение

x3=(x-2)2,откуда x=1;

• 4)    вычислить площадь фигуры по формуле (4):

В случае, когда кривая, ограничивающая фигуру, задана в полярных координатах т=ф(9), а<9<р,

Рис. 6. Фигура к примеру 4.

5 (х — 2)2dx = -.

где ф(9) - непрерывная на отрезке [а,р] функция,то площадь фигуры вычисляется по формуле

1 гР

-  v2(e)d6.

Если фигура симметрична относительно полярной оси, то достаточно вычислить площадь верхней половины по формуле (5), а затем удвоить полученный результат. Рассмотрим пример.

П р и м е р 5. Найти площадь фигуры, ограниченной улиткой Паскаля r=2a(2+cosθ).

оси, то достаточно вычислить

Так как кривая симметрична относительно полярной площадь верхней половины.

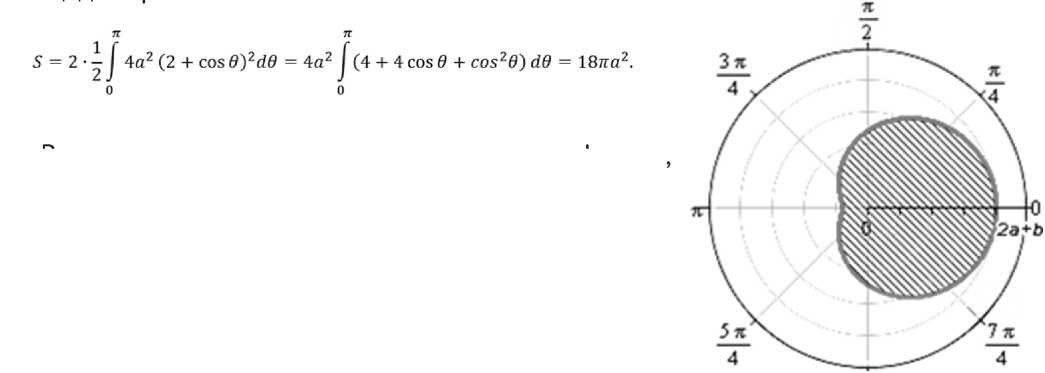
то площадь фигуры вычисляется по формуле

Рис. 7. Улитка Паскаля.

В случае, когда кривая, ограничивающая фигуру, задана параметрическими уравнениями

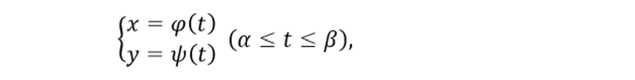
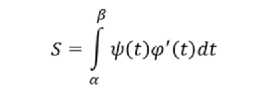
При вычислении площади фигуры, ограниченной замкнутой кривой по формуле (6), необходимо учитывать, что вся кривая обходится один раз по направлению вращения часовой стрелки, когда параметр t изменяется от α до β.

П р и м е р 6. Вычислить площадь эллипса х = a cost, у = b sint,

Для решения задачи необходимо выполнить следующие действия:

• 1)    построить фигуру по данным задачи (Рис. 8);

• 2)    установить симметричность фигуры (так как она ограничена замкнутой кривой); ввиду симметрии кривой относительно осей координат достаточно

вычислить площадь части эллипса, находящейся в первой четверти;

• 3)    найти пределы интегрирования, так как x=a cost изменяется в первой четверти от 0 до а, то , соответственно, будет изменяться от π/2 до 0;

• 4)    вычислить площадь фигуры по формуле (6):

  

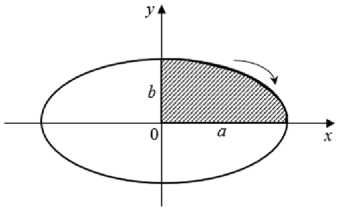
  Рис. 8. Эллипс.

  
  
  
  
  

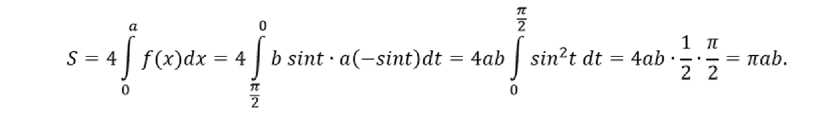
Состав действий методов вычисления фигуры в полярных координатах и при параметрическом задании кривой представлен в виде схемы на Рис. 9.

По такой же схеме, выделяя отдельные компоненты и рассматривая разные случаи, можно обучать студентов другим методам математического анализа, представленным не только в разделах дифференциального и интегрального исчислений, но и в других его разделах.

Усвоение студентами педвуза математических методов важно с разных точек зрения. С общеобразовательной точки зрения они выполняют функцию обобщения и

Рис. 9. Деятельностный состав методов вычисления площадей фигур, заданных в полярных координатах и параметрически.

8

ОС

Я

В

ч

д

о

о

к

Я

О

я

PQ

систематизации тех знаний, которые связаны с данным методом. Мировоззренческое значение методов заключается в том, что они выполняют интегрирующую функцию: с одной стороны, появляется возможность показать проникновение математики в другие науки, в практику, с другой стороны, выделить то общее, что объединяет все методы математики (единый подход в применении, этапы применения и т. д.). Кроме того, появляется возможность для раскрытия содержания понятия «метод» и выделения его компонентов, что очень важно для будущих педагогов в методологическом отношении.