Методические особенности организации лабораторных работ по физике на примере определения модуля юнга различных веществ в общеобразовательной школе

В процессе обучения в школе выполнение лабораторной работы учащимися является формой образовательных    технологий, способствующей формированию у учащихся комплекса компетенций:

• -    способность к познавательной деятельности;

• -    способность применять навыки работы с информацией из различных источников для решения задач и др.

Заметим, при выполнении лабораторной работы, учащийся должен понимать физический смыл процесса, представленного в лабораторной работе. Поэтому к выполнению работы нужно приступать только после изучения теоретического материала.

С учетом представленной к рассмотрению тематики в данной статье, отметим, что как кристаллические, так и аморфные твердые тела имеют свойство изменять свою форму под воздействие приложенной к ним силы, - деформироваться. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела есть предел приложенного усилия, после которого деформация перестает быть упругой, т.е. тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии.

Теория упругих деформаций была создана в конце XVII века ученым Р. Гуком и развита в трудах Т. Юнга. Модуль Юнга есть важная механическая характеристика вещества. Во время принудительного изменения формы предметов внутри них активизируются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел. Если тело не оказывает сопротивления изменению формы и остается в деформированном виде, то такое тело называют абсолютно неупругим.

Величина, которая характеризует сопротивление материала к растяжению, т.е. увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем упругости. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Обозначается как E; измеряется н/м2 или в Па.

Отметим, модуль Юнга показывает зависимость относительного удлинения от нормальной составляющей силы (F) к ее площади распространения (S) и упругости (Е). Модули упругости для различных материалов имеют разные значения, зависящие:

• -    от природы веществ, формирующих состав материала;

• -    от состава: моно- или многокомпонентный;

• -    структуры (вид кристаллической решетки, молекулярное строение);

• -    плотности материала;

• -    обработки, которой подвергался материал (обжиг, травление, и

• т.п.).

Так, модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Для отожженного алюминия модуль Юнга – 68,5 ГПа. Для железа показатель напряжения к деформации зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа. Для стали модуль упругости может достигать 235 ГПа. Заметим, на величины параметров прочности влияют также формы изделий..

Представим методику выполнению лабораторной работы на определение модуля Юнга. Цель работы - определить модуль Юнга стали.

Стальная проволока 1 растягивается под действием переменных грузов 4 (рис. 1). Длина проволоки ^ измеряется линейкой 2, ее диаметр d– микрометром, абсолютное удлинение А/ – индикатором 3.

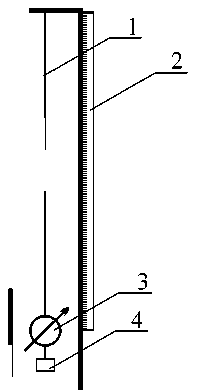
Рис. 1 Установка для измерения модуля Юнга стальной проволоки

Представим методику выполнения работы:

• 1.    Нагрузив проволоку грузами для ее выпрямления, сделать отсчет по индикатору длин.

• 2.    Провести контрольные измерения величин l,d,m, входящих в уравнение:

• 3.    Результаты измерений занести в таблицу 1.

• 4.    Оценить относительную случайную погрешность величины ^a методом наименьших квадратов.

• 5.    Определить модуль Юнга проволоки.

• 6.    Оценить полную относительную погрешность косвенных измерений модуля Юнга проволоки.

_ F M 4mql

E= — ; — = —

S 1 Kd2M

где d - диаметр растягиваемой проволоки, ^ - ее длина.

Таблица 1 - Результаты измерений и расчетов для определения модуля продольной упругости проволоки

Итак, мы представили методические указания к порядку выполнения лабораторной работы на определение модуля Юнга и обработки полученных результатов измерений.