Методика и результаты оптимизации параметров сложнонагруженных подшипников скольжения
Автор: Прокопьев Валерий Никифорович, Гаврилов Константин Владимирович
Рубрика: Расчет и конструирование
Статья в выпуске: 11 (83), 2007 года.
Бесплатный доступ
Приводится методика и результаты решения задачи оптимизации конструктивных параметров сложнонагруженных подшипников скольжения. Поле гидродинамических давлений в смазочном слое подшипников определяется интегрированием модифицированного уравнения Элрода. Показано, что выбором оптимальных параметров, прежде всего, вязкостно-температурной зависимостью масла, можно существенно улучшить все гидромеханические характеристики, определяющие износостойкость подшипников, усталостную долговечность антифрикционного слоя, потери на трение.
Короткий адрес: https://sciup.org/147151395
IDR: 147151395
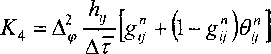
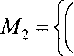
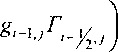
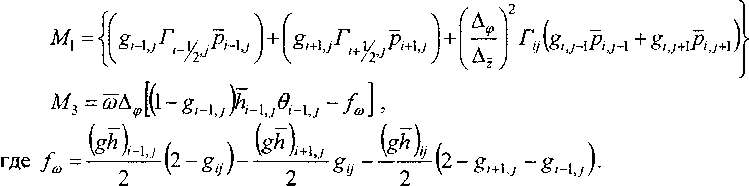
Список литературы Методика и результаты оптимизации параметров сложнонагруженных подшипников скольжения
- Соболь И.М. Выбор оптимальных параметров в задачах со многими критериями/И.М. Соболь, Н.Б. Статников. -М.: Наука, 1981, -285 с.
- Прокопьев В.Н. Повышение эффективности алгоритмов расчёта выходных параметров сложнонагруженных опор скольжения двигателей транспортных машин/В.Н. Прокопьев, Ю.В. Рождественский, Н.В. Широбоков//Вестник УМОАТ. -Курган, 1999. -№ 2. -С. 28-32.
- Элрод. Алгоритм расчёта зоны кавитации/Элрод//ТАОИМ. -М.: Мир. Серия Ф. Проблемы трения и смазки. -1981. -№ 3. -С. 28-32.
- Прокопьев В.Н. Модификации алгоритма Элрода и их применение для расчёта гидродинамических давлений в смазочных слоях сложнонагруженных опор скольжения/В.Н. Прокопьев//Вестник ЮУрГУ. Серия «Машиностроение». -2001. -Вып. 1. -№ 6 (06). -С. 52-60.
- Прокопьев В.Н. Применение алгоритмов сохранения массы при расчёте динамики сложнонагруженных опор скольжения/В.Н. Прокопьев, А.К. Бояршинова, К.В. Гаврилов//Проблемы машиностроения и надежности машин. -М.: Наука, 2004. -№ 4. -С. 32-38.
- Прокопьев В.Н. Применение при расчете гидромеханических характеристик сложнонагруженных подшипников алгоритма сохранения массы/В.Н. Прокопьев, К.В. Гаврилов//Труды международного научного симпозиума «Гидродинамическая теория смазки -120 лет». В 2-х томах. -М.: Машиностроение, Орел: ОрелГТУ, 2006. -Т. 1. -С. 330-339.
Статья научная
