Методика изучения физических эффектов, используемых для измерения давления

Четвертая промышленная революция [1] набирает ход, при этом особое внимание привлекают к себе датчики измерения физических величин (ФВ), в частности, датчики давления. Принцип работы таких датчиков основан на использовании различных физических эффектов (ФЭ), которые обладают определенной спецификой применения. Физический эффект – это закономерность проявления результатов взаимодействия объектов материального мира, осуществляемого посредством физических полей [2]. Исследования ФЭ являются одним из основных направлений в приборостроении при разработке, создании и изучении новых датчиков давления [3], а также в учебном процессе по направлению подготовки 12.03.01 «Приборостроение».

Однако описания физических эффектов в литературных источниках [4–6] с точки зрения их изучения характеризуются отсутствием четкой структуры изложения свойств и характеристик эффектов. Таким образом, актуальной является задача создания методики изучения ФЭ на примере датчиков давления.

Методика изучения ФЭ

Предложим следующую методику описания физических эффектов, используемых для создания датчиков измерения давления. Она имеет следующий вид:

• 1)    описание математической модели физического эффекта;

• 2)    описание физической реализации данного эффекта;

• 3)    представление зависимости выходного сигнала датчика давления от входной величины;

• 4)    графическое представление данной зависимости;

• 5)    конструктивная реализация физического эффекта в датчике.

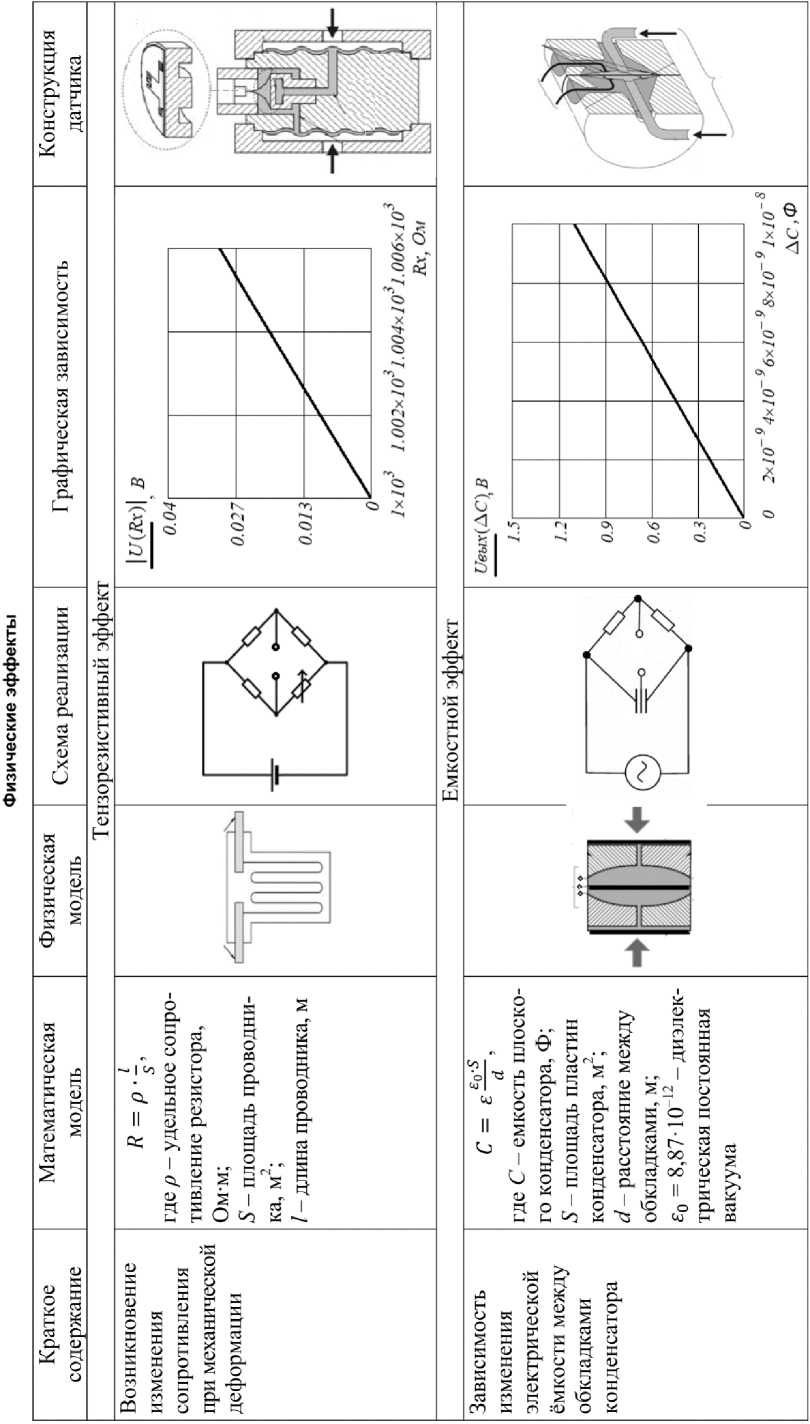
Данная методика имеет такие преимущества, как наглядность и простоту изложения. Проиллюстрируем данную методику на примере тензорезистивного и емкостного эффектов.

Тензорезистивный эффект

Тензорезистивный эффект основан на изменении сопротивления проводника при его механической деформации (растяжении) [7].

Сопротивление проводника определяется по следующей формуле [7]:

R = p--,

s,

где R – сопротивление проводника, Ом;

• ρ – удельное сопротивление проводника, Ом ⋅ м;

• S – площадь поперечного сечения проводника, м²;

l – длина проводника, м.

Рассмотрим проводник, на который действуют внешние силы F (рис. 1).

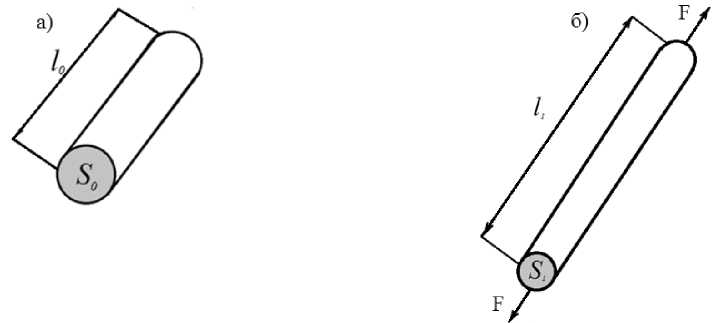
Рис. 1. Воздействие силы на проводник: а – проводник в исходном состоянии; б – проводник в деформированном состоянии

Проволочный тензорезистор, используемый в датчике, состоит из отрезка провода, согнутого в форме серпантина и смонтированного на подходящем материале подложки [5] (рис. 2).

Обычно для реализации тензорезистивного эффекта при измерении давления используется мост Уитстона [7]. Схема моста Уитстона представлена на рис. 3.

Выводы датчика к проволочным

Проволочный датчик

Бумажная подложка (изолятор)

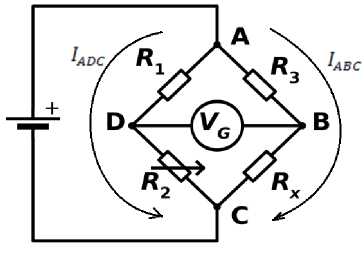
Рис. 3. Мостовая схема Уитстона, используемая в датчиках давления: R 1 , R 2 , R 3 – резисторы, номиналы которых известны; V G – гальванометр; R x – тензорезистор

Рис. 2. Тензорезистор

Тензорезистор Rx крепится на элемент, подверженный деформации при изменении давления, чаще всего путем наклеивания тензорезистора на мембрану датчика, которая прогибается под воздействием давления [7]. Полезным сигналом в данном случае является изменение напряжения на измерительной диагонали моста (между точками B и D). Если выполняется равенство (1), то мост находится в состоянии равновесия, следовательно, напряжение UDB на измерительной диагонали будет равно нулю:

^ = ^.

R2

Выразим напряжение измерительной диагонали U DB моста через сопротивления плеч и напряжение питания U_AC моста [7]:

Udb = Фо - фв = ^Фс + Ur2^- (фс + Urx^ = Ur2 - Urx;(2)

UDB = ^ADC • R2 - ^ABC • Rx;

UDb = "^ • R2 - -^^^ • Rx = Uc • ^^«^).(4)

^DB   R_±+R₂   ² R₃+R_x ^{х     AC}    R i +R₂   R₃+R_x

Для примера будем использовать тензорезистор ФКП-3-1000 (1000 Ом) [8]. Согласно паспортным данным ^R_MAX максимальное изменение сопротивления от номинального составляет 6 Ом [8, 9]. В соответствии с номиналом тензорезистора и условием равновесия подбираются остальные параметры моста: R 1 = 1000 Ом, R 2 = 1000 Ом, R 3 = 1000 Ом, и зададим напряжение питания U AC = 20 В.

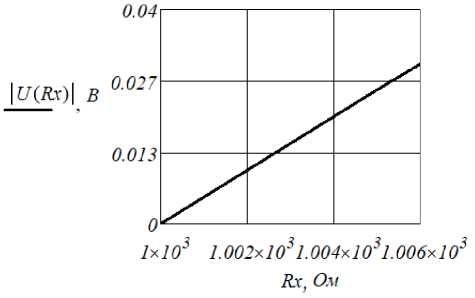
Рис. 4. График зависимости |U DB | = f ( R x )

Проверим правильность подбора элементов моста по выражению (4):

^U db

= 20 • ^

1000 +1000

-

1000 +1000

) = 0 В.

Получим зависимость напряжения измерительной диагонали как функцию от сопротивления тензорезистора U DB = f ( R x ):

^U db

= 20 • (

1000+1000

-

^R x 1000 +R x

).

Представим зависимость |U DB | = f ( R x ) графически (рис. 4).

Схема Уитстона реализуется в датчике [7], конструкция которого представления на рис. 5.

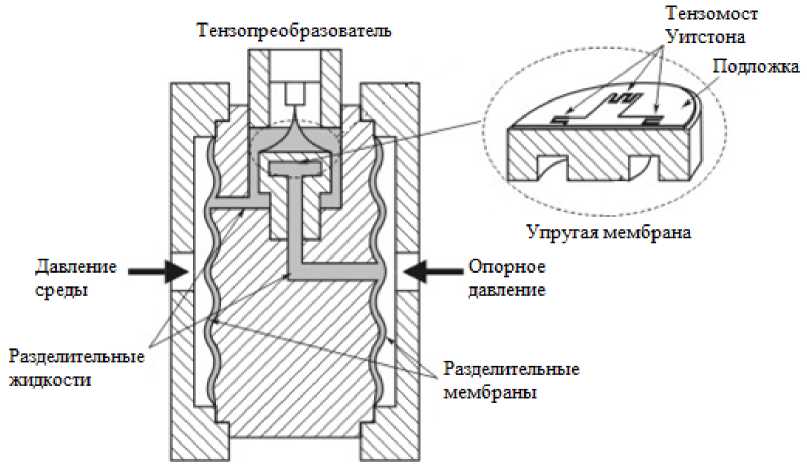
Рис. 5. Конструкция тензорезистивного датчика

Емкостной эффект

Емкостной эффект возникаетпри изменении емкости конденсатора вследствие изменения расстояния между обкладками либо их площади [10, 11].

Выражение для емкости плоского конденсатора [8]:

С=е^ ,                                                    (5)

где C – емкость плоского конденсатора, Ф;

S – площадь пластин конденсатора, м²;

• d – расстояние между пластинами, м;

• ε – относительная диэлектрическая проницаемость материала диэлектрика;

• ε 0 = 8,87·10^–12 – диэлектрическая постоянная вакуума, Ф/м.

На рис. 6 приведен чувствительный элемент датчика давления, использующий функциональную зависимость С ( d ) [10].

Рис. 6. Конденсатор: а – без воздействия сил на обкладки; б – под воздействием сил F на обкладки

Ключевым элементом в емкостном датчике давления является емкостная ячейка, которая имеет конструкцию, представленную на рис. 7.

Для измерения давления с использованием емкостного эффекта используем мост Саути [10], представленный на рис. 8.

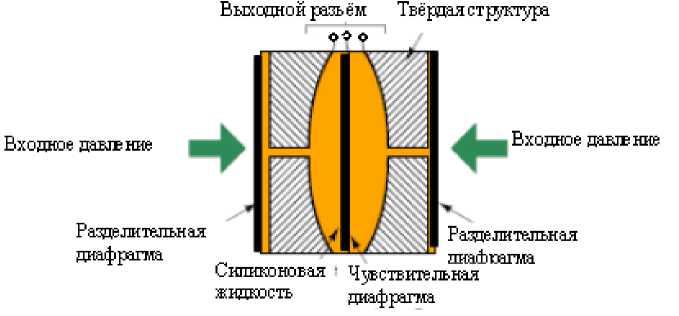
Рис. 7. Конструкция емкостной ячейки

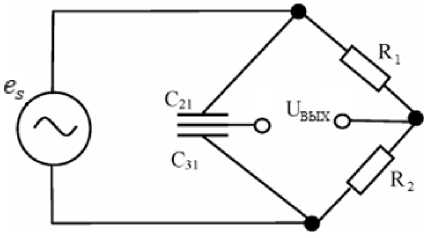
Рис. 8. Схема моста Саути: C ₂₁ , C ₃₁ – конденсаторы с неизвестной емкостью;

R 1 , R 2 – резисторы известных номиналов; e s – переменный источник питания

Для моста переменного тока условие баланса выполняется следующим соотношением импе-дансов:

£i _ £з z2    Z4’

где z ; - импеданс i -й ветви.

Напряжение на выходе измерительной схемы имеет вид [4]:

£ s ^С21 ^{— С}31

Ц зых = ₂ ■ _С21_{+ С 3} 1 ,

где C 21 , C 31 – емкости конденсаторов емкостной ячейки, Ф;

e_s - напряжение источника питания, В.

Зададим конкретные номиналы элементов электрической схемы: R ₁, R ₂ = 1 кОм, C ₂₁, C ₃₁ = 1 мкФ, e s = 220 В, w=100 рад/с.

Проверим условие равновесия моста по формулам (6) и (7) соответственно:

1              1

IWC21    bw^C3i

R 2    ~ Ri ’

1 = 1 - равенство выполняется,

U вых

S s • С 21 — С 31

2 С21 + С31

220 10 "⁶ —10 "⁶

2   10 "⁶ +10 "⁶

Получим зависимость U _аых = f ДС) по формуле (7):

Цвых

S_s С₂₁—С₃₁ _ 220 (10 "⁶ +ДС) — (10 "⁶ —ДС) 2 С₂₁+С₃₁ = 2 (10 "⁶ +ДС)+(10 "⁶ —ДС)

1,1-108-ДС,

где ДС - изменение ёмкостей конденсаторов C ₂₁ и C ₃₁, Ф.

Графическая зависимость U в _ых = f (ДС) представлена на рис. 9.

Электрическая схема реализуется в сенсоре, представленном на рис. 10.

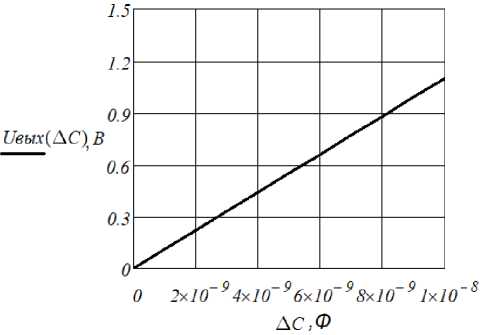
Рис. 9. Графическая зависимость U вых = f ( ∆C )

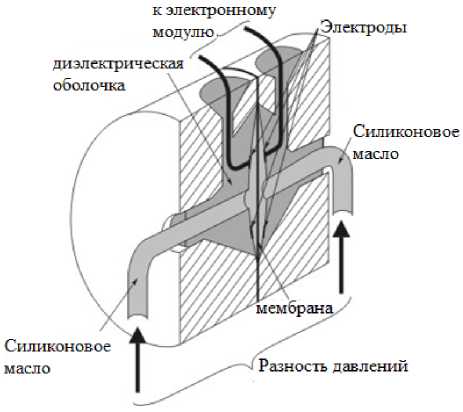
Рис. 10. Измерительный преобразователь емкостного датчика давления

Заключение

Таким образом, мы продемонстрировали методику изучения физических эффектов на примере ёмкостного и тензорезистивного (см. таблицу), содержащую этапы: описание математической его модели, описание физической реализации, описание зависимости выходного сигнала датчика от входной величины, графическое представление данной зависимости, конструктивную реализацию физического эффекта в датчике.