Методика организации групп обучающихся среднего профессионального образования для подготовки к олимпиадам по математике
Бесплатный доступ
Статья посвящена значению олимпиады по математике среди студентов среднего профессионального образования. Определены проблемы, которые существуют в настоящее время в организации подготовки студентов к математическим олимпиадам. Приведен пример опытно-экспериментальной работы, позволяющий определить группу обучающихся, с которыми можно организовать подготовку к математическим олимпиадам.
Среднее профессиональное образование, математическая олимпиада, образовательный процесс
Короткий адрес: https://sciup.org/140287984
IDR: 140287984 | УДК: 372.851
Methodics of organizing groups of students of secondary vocational education for preparation for Olympiads in mathematics
The article is devoted to the significance of the mathematics Olympiad among students of secondary vocational education. The problems that currently exist in the organization of preparing students for mathematical olympiads are identified. An example of experimental work is given, which allows to determine the group of students with whom you can organize preparation for mathematical olympiads.
Текст научной статьи Методика организации групп обучающихся среднего профессионального образования для подготовки к олимпиадам по математике
В век информационного общества естественно-математические знания становятся более востребованы. Благодаря тщательным подготовкам к олимпиадам по математике знания студентов пополняются. Олимпиады способствуют формированию мотивации у обучающихся. Термин «олимпиада» означает выявление способностей, которые открываются во время применения практических навыков в части определённой дисциплины. Особенностью олимпиады является раскрытие творческих способностей, которые проявляются во время специальной формы проведения студенческой олимпиады [1].
Почему возникает необходимость участия в олимпиадном движении и введение его в систему обучения и воспитания обучающихся? Участие в олимпиадном движении формирует у молодых людей ответственность за начатое дело, целеустремленность, трудолюбие, патриотизм. Олимпиада по математике - форма интеллектуального соревнования, которая позволяет выявить не только знания фактического материала, но и умение применять эти знания в новых нестандартных ситуациях, которые требуют творческого мышления [2].. Направлена она на повышение качества среднего профессионального образования в интересах развития личности, обеспечение профессиональной мобильности выпускников, достижение высокого профессионального мастерства.
Произошли существенные изменения, которые требовали новых подходов в методике подготовки и проведения математических олимпиад.
Несмотря на то, что накоплен большой опыт проведения олимпиад, в этом направлении сохраняется ряд противоречий:
-
- между социальным заказом общества на подготовку обучающихся к математическим олимпиадам в среднем профессиональном образовании и недостаточно эффективными способами организации образовательного процесса для продуктивного решения этой задачи;
-
- между результатами педагогических исследований и недостаточно разработанностью направлений и программ обучения при подготовке к математическим олимпиадам.
-
- между математическими знаниями обучающихся и требований, предъявляемых к этим знаниям на олимпиадах.
Для работы над устранениями этих проблем сначала необходимо ответить на вопрос: «С кем осуществлять подготовку к олимпиадам по математике?».
Подготовка к олимпиадам по математике является главным этапом. Преподаватель, подготавливая обучающихся к олимпиадам по математике, готовит их к жизни, помогает справиться с трудностями, обучая принятию самостоятельных решений. Благодаря этому происходит воспитание личности, которое готовит к жизни в конкурентном мире.
Рассмотрим один из способов, как можно отобрать группу обучающихся для организации подготовки к математическим олимпиадам. Проводимую работу опишем на примере группы P. Обучающимся предлагались 12 задач разного уровня сложности, которые относилисья к различным темам. За правильное выполнение каждого задания обучающийся получает по 1 баллу. В результате за 12 заданий можно набрать 12 баллов. Результаты отражены в таблице 1.
Таблица 1
Уровень знаний обучающихся группы P
|
Обучающиеся |
Номер задания |
Кол-во баллов |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
P1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
10 |
|
P2 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
7 |
|
P3 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
8 |
|
P4 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
7 |
|
P5 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
P6 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
6 |
|
P7 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
9 |
|
P8 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
7 |
|
P9 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
7 |
|
P10 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
|
P11 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
12 |
|
P12 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
8 |
|
P13 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
10 |
|
P14 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
5 |
|
P15 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
12 |
|
P16 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
7 |
|
P17 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
10 |
|
P18 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
9 |
|
P19 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
10 |
|
P20 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
7 |
|
Кол-во обучающихся, справившиеся с заданием |
18 |
13 |
19 |
16 |
18 |
7 |
9 |
16 |
8 |
16 |
11 |
7 |
Результаты представим в виде диаграммы «Распределение количества баллов» Диаграмма нам понадобится для определения количества обучающихся в соответстсвии с набранными баллами.
Распределение количества баллов
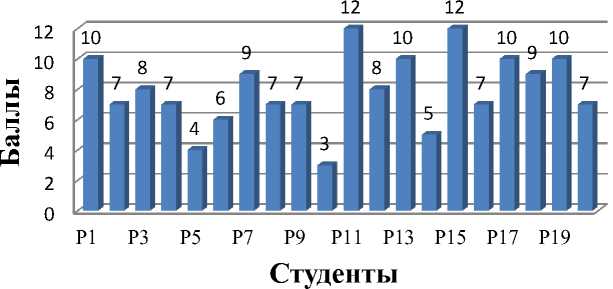
Рис.1. Распределение количества баллов группы Р
При помощи диаграммы определим, сколько студентов набрали то или иное количество баллов. Результаты отобразим в таблице 2.
Уровень знаний обучающихся
Таблица 2
|
Кол-во баллов |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Число |
0 |
0 |
1 |
1 |
1 |
1 |
6 |
2 |
2 |
4 |
0 |
2 |
|
студентов |
||||||||||||
|
% отношение |
0 |
0 |
5 |
5 |
5 |
5 |
30 |
10 |
10 |
20 |
0 |
10 |
Для наглядности результаты представим в виде диаграммы:
% отношение
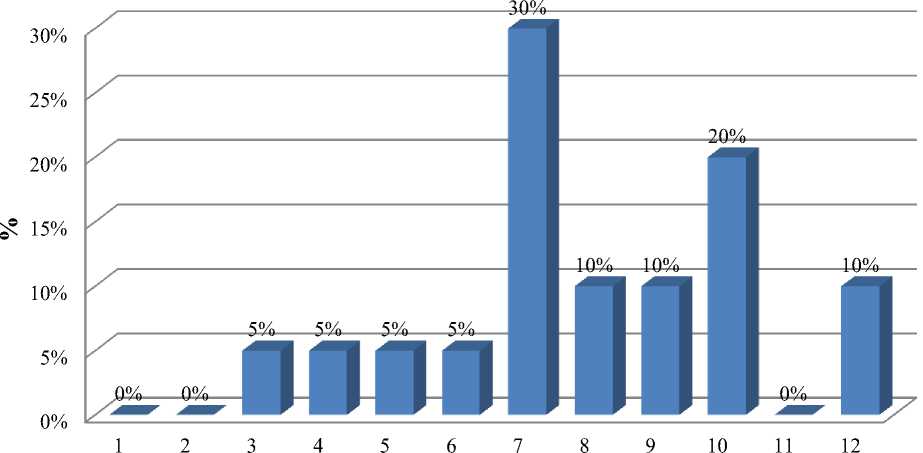
Баллы
Далее, определим 3 уровня: низкий уровень – от 1 до 6 баллов, средний уровень – от 7-9 баллов, высокий уровень – от 10до 12 баллов.
Получим предварительно следующую таблицу 3.
Таблица 3
Уровень знаний
|
Низкий |
Средний |
Высокий |
|
4 (20%) |
10 (50 %) |
6 ( 30%) |
Результаты таблицы отразим на диаграмме:
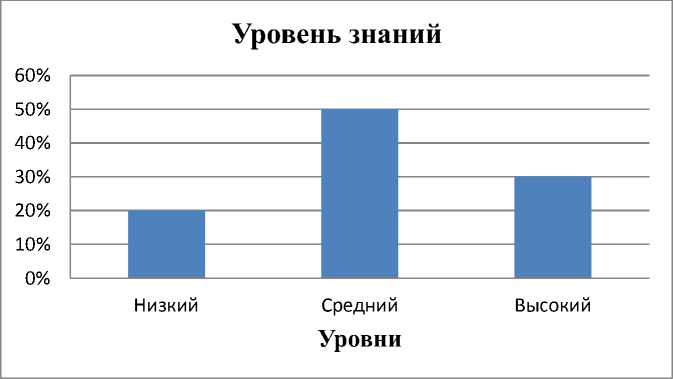
Рис.2. Уровень знаний студентов группы Р
Таким образом, мы можем сделать вывод, что минимум с 6-ю студентами можно организовать подготовку к математическим олимпиадам.
Список литературы Методика организации групп обучающихся среднего профессионального образования для подготовки к олимпиадам по математике
- Алексеева Г.И. Из истории становления и развития математических олимпиад (Опыт и проблемы): Дис.. канд. пед. Наук - Якутск, 2002 - 144 с.
- Соломин В.П., Махов С.И., Ильинский С.В.Некоторые подходы к разработке заданий заключительного этапа всероссийских олимпиад школьников // Вестник Герценского университета, РГПУ им. А.И. Герцена - 2013 г. - № 4. - С. 133-138.
