Методика построения контрольно-обучающих программ и их использование в преподавании математических дисциплин

Обучающая программа и программированное обучение. Использование обучающих программ – один из наиболее действенных и интересных методов, применяемых для организации самостоятельной работы студентов и при дистанционном обучении. Прежде всего уточним само понятие обучающей программы. Хотя данный термин является достаточно употребительным, понимается он не совсем однозначно. Мы определяем обучающую программу как разветвленную последовательность порций материала, «усваиваемых» по некоторому алгоритму, зависящему, в том числе, и от действий учащегося. Обучающая программа может относиться к разным категориям. Это может быть программа-тренажер, интерактивная учебная система, обучающая игра и др. Она также может сочетать все перечисленные качества и выполнять как тренинговые, так и тестовые функции. Главное условие – программа устроена так, что она получает информацию об обучаемом и, в зависимости от этой информации, направляет его определенным образом.

Обучающая программа является инструментом образовательной технологии, называемой программированным обучением. Концепция программированного обучения возникла в начале 50-х гг. XX в., когда американский психолог Беррес Скиннер (1904-1990) предложил повысить эффективность усвоения материала, выстраивая его как последовательную программу подачи порций информации и контроля за их усвоением. Скиннер рассматривал обучение в соответствии с классической схемой бихевио- ризма «стимул – реакция – подкрепление», которую в данном случае следует понимать так: обучаемому предъявляется порция учебного материала; он определенным образом действует с этим материалом; действия оцениваются (критикуются или поощряются), что делает усвоение эффективным. В рамках линейного алгоритма, предложенного Скиннером, ученик движется достаточно мелкими шагами, каждый шаг обязателен, возврат к прежним шагам исключается.

Эти особенности линейной программы вызвали критику программированного обучения за то, что такая жесткая схема не позволяет ученику видеть общей цели, сковывает его инициативу и самостоятельность. Создатель разветвленных программ Н.А. Краудер (1921-1998) считал, что дозы учебной информации должны быть достаточно большими, поскольку для усвоения важен не безошибочный путь мелкими шагами, а глубокий, всесторонний анализ материала. Другая особенность разветвленной программы – разнообразие вариантов ответа ученика. Он выбирает ответ на контрольный вопрос из предложенного набора, где есть не только правильный, но и неполные и неверные ответы, содержащие типичные ошибки. Если ученик выбрал правильный ответ, он переходит к следующему шагу. В противном случае ему разъясняется сущность ошибки, и он получает указание вернуться к исходному пункту, возможно, получив подсказку. Таким образом, разветвленная программа ведет обучаемых разными путями в зависимости от их ответов и ошибок.

Однако и у такой программы есть недостатки. Критики обучающих программ, построенных на данном принципе, считают, что выбор ответа провоцирует ученика угадывать и запоминать правильные ответы и исключать ошибочные, то есть обучающая программа такого рода тоже не дает ученику цельного и системного представления о материале. Согласимся с тем, что идеальных средств обучения не существует, однако заметим, что многое зависит не только от алгоритма программы, но и от ее конкретного наполнения, т.е. от искусства разработчика обучающих материалов. Большое значение имеет также мотивация самого обучаемого: настроен ли он на полноценное критическое усвоение информации, или склонен к угадыванию и «зазубриванию».

В нашей стране вклад в разработку теории программированного обучения был внесен Н.Ф. Талызиной, В.П. Беспалько, П.Я. Гальпериным, И.Е. Шварцем и другими [1, 2]. Отметим также ряд диссертационных исследований последнего десятилетия, связанных с проблемами программированного обучения и применения обучающих программ [3-6].

Принципы и средства программированного обучения. Согласно имеющейся литературе по программированному обучению (например, [2, 7]), оно опирается на несколько основных принципов.

Первый принцип - иерархия управляющих устройств. Педагог управляет системой в наиболее ответственных ситуациях: создание предварительной общей ориентировки в предмете, индивидуальная помощь и коррекция в сложных и/или нестандартных ситуациях обучения.

Второй принцип – деление материала на малые части (шаги). Программированный учебный материал представляет собой серию сравнительно небольших порций учебной информации, подаваемых в определенной логической последовательности.

Третий принцип - обратная связь. Имеется в виду, что кроме передачи информации о необходимом образе действия от управляющего объекта к управляемому (прямая связь), есть и передача информации о состоянии управляемого объекта управляющему (обратная связь).

Четвертый принцип – индивидуальный темп в обучении. Работа обучаемого по программе строго индивидуальна, каждому предоставляется возможность продвигаться в учении со скоростью, которая для его познавательных сил наиболее благоприятна.

Пятый принцип – адаптация. Управляющая программа должна приспосабливаться к индивидуальным способностям ученика, организовывать поддержку, подсказку, применять наводящие вопросы и т.д. Это требует использования специальных средств для работы с программированными учебными материалами, моделирующими с любой степенью полноты деятельность педагогов в процессе обучения.

Средства программированного обучения достаточно разнообразны. Это могут быть программированные печатные (бумажные) пособия, электромеханические устройства, компьютерные обучающие средства.

Разумеется, наибольшие возможности для программированного обучения дают современные компьютеры. Они позволяют создавать сложные электронные системы обучения, которые обладают большими дидактическими возможностями. В частности, разрабатываются интерактивные программы, в которых обучаемый работает в диалоговом режиме со сложными информационными системами, базами данных, экспертными системами, выполняющими дидактические функции.

Диалоговый принцип работы обучающей программы. По нашему мнению, предпочтительной основой компьютерных обучающих программ является принцип активного диалога между студентом и компьютером. Например, компьютер «задает» студенту вопросы, принимает его ответы, дает аргументированные комментарии к ним и с помощью некоторых подсказок или «намеков» способствует отысканию истины. Этот алгоритм, принципиально соответствующий концепции разветвленной программы Краудера, отображен на рисунке 1.

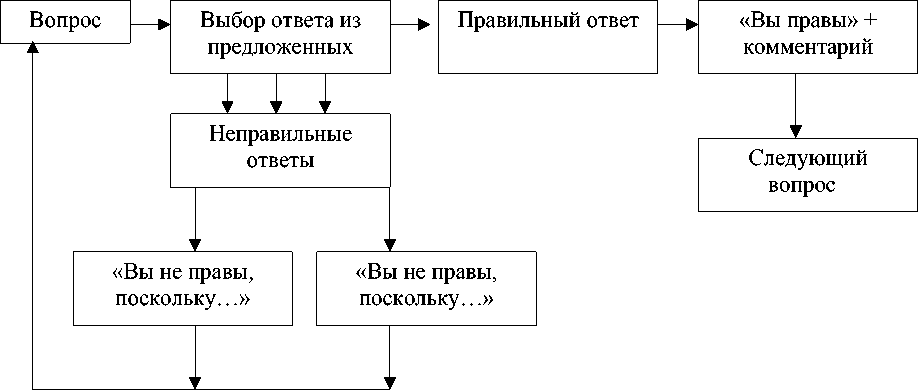
Рис. 1. Блок-схема обучающей программы, работающей в диалоговом режиме (вариант 1: «ищем истину»)

В качестве примера реализации данного алгоритма приведем фрагменты обучающей программы по теории вероятностей.

Задание. Какое из перечисленных ниже равенств является необходимым и достаточным условием независимости события A от события B ?

Первый вариант ответа . P ( A ) * P ( B ).

Комментарий. Вы не правы. Из того, что два события имеют разную вероятность, вовсе не следует, что они независимы. Например, при выборе одной карты из 36 событие A - появление дамы - происходит с вероятностью 1/9; событие B - появление пиковой дамы - с вероятностью 1/36. Но ведь событие A зависит от со- бытия B. Действительно, если известно, что со- бытие B произошло, то событие A имеет веро- ятность 1, т.е.

р(ab) = 1. Если известно, что со- бытие B не произошло, то событие a имеет вероятность 3/35. Иначе говоря, условные вероятности события A не равны его «безусловной» вероятности P(A) = 1/ 9 .

Второй вариант ответа . р ( A ) + P ( B ) = 1 .

Комментарий. Вы не правы. Выбранное Ва- ми равенство справедливо для двух противопо- ложных событий (A = B), но не имеет никакого отношения к определению независимости событий.

Третий вариант ответа. р ( ab ) = P ( B| A ) .

Комментарий. Вы не правы. Пример. Бросаются 2 игральные кости. Событие A - выпадение «шестерки» на 1-й кости, событие B - выпадение нечетной цифры на второй кости. P(AB) = 1/6, P(BA) = 1/2. Таким образом, P(AB) * P(BA), но события явно независимы. Обратите внимание: здесь р ( ab ) = P (A), P(BA) = P(B). Это означает, что в данном случае «условность» вероятностей теряет смысл.

Четвертый вариант ответа .

P ( BB ) = P ( A )

Комментарий. Вы правы . Для независимых событий условные вероятности не отличаются от «безусловных».

Приведенный фрагмент содержит обсуждение вопроса, имеющего теоретический характер. Однако в рамках обучающей программы может обсуждаться и конкретная практическая задача.

Задание. Имеется 2 билета разных лотерей. Вероятность выигрыша в первой лотерее равна 0.01, а во второй 0.02 . Как найти вероятность того, что один из этих билетов выиграет, а один проиграет?

Первый вариант ответа . Надо рассмотреть две гипотезы: H ₁ – выиграет первый билет, P ( h 1 ) = 0.01 ; h 2 - выиграет второй билет, P ( H 2 ) = 0.02 . После этого, считая, что P ( AH 1 ) = 1/2, P ( A|H ₂) = 1/2 , следует применить формулу полной вероятности.

Комментарий . Вы не правы. Учтите, что гипотезы должны образовывать полную группу несовместных событий. Следовательно, сумма их вероятностей должна быть равна единице.

Второй вариант ответа . Событие A ₁ (билет первой лотереи выиграет) – вероятность P ( A 1 ) = 0.01 , событие a 2 (билет второй лотереи выиграет) имеет вероятность P ( A 2 ) = 0.02. Событие A i • A 2 заключается в проигрыше обоих билет ов. Его вероятность равна

P ( A • A 2 ) = P ( A ) P ( A 2 ) = 0.99 • 0.98 = 0.9702.

Нас интересует событие «из двух билетов один оказался выигрышным». Вероятность этого события равна 1 - 0.9702 = 0.0298.

Комментарий . Вы нашли вероятность события, противоположного проигрышу обоих билетов. Это – не что иное, как вероятность того, что выиграет хотя бы один (т.е. один или более) билет. Перечитайте условие задачи: там речь идет о выигрыше не хотя бы одного, а ровно одного билета!

Третий вариант ответа . Надо рассмотреть две гипотезы: H ₁ – куплен билет первой лотереи, P ( H 1 ) = 0.5 ; H ₂ — куплен билет второй лотереи, P ( H ₂) = 0.5. После этого следует применить формулу полной вероятности считая, что P ( A\H 1 ) = 0.01, P ( AH ₂) = 0.02 .

Комментарий . Вы не правы . По условию задачи куплено по одному билету каждой лотереи. По логике выбранного Вами решения покупается один билет – тогда действительно имело бы смысл рассматривать гипотезы (покупка билета первой лотереи и покупка билета второй лотереи). Таким образом, выбранное Вами решение не соответствует предложенной задаче.

Четвертый вариант ответа. Событие A1 (билет первой лотереи выиграет) имеет вероятность P(A1) = 0.01, событие a2 (билет второй лотереи выиграет) имеет вероятность P(A2) = 0.02. Нас интересует событие «из двух билетов один и только один оказался выигрыш- ным», т.е. A1 A2 + A1 A2.

В ероятн ость этого события равна P ( A ! A 2 + AA ₂ ) = 0.01 • 0.98 + 0.99 • 0.02 = 0.0296 .

Комментарий . Вы правы. Предложенную задачу можно было решить и другим способом. Пусть событие A – выиграли оба купленных билета, событие B – проиграли оба купленных билета, событие C – один билет выиграл и один проиграл. Тогда

P ( C = 1 - P ( A ) - P ( B ) = 1 - 0.01 • 0.02 - 0.99 • 0.98 = 0.0296

Другая возможная схема построения обучающей программы: перед студентом ставится задача, которая должна быть решена в несколько действий (шагов). Каждый шаг считается сделанным лишь после того, как будет выбран правильный вариант из предложенных вариантов действия. Задание считается выполненным, если выбрана полностью правильная последовательность шагов. Этот алгоритм отображен на рисунке 2. Принципиально он близок к концепции линейной программы Скиннера.

В качестве примера рассмотрим фрагмент обучающей программы по аналитической гео- метрии.

Задание . Требуется найти линию, каждая точка которой находится вдвое ближе к точке A ( - 1; 0), чем к прямой L , имеющей уравнение x = - 4 .

Шаг 1 . Из приведенных изображений выберите то, которое соответствует условию. (Приведено несколько изображений; одно из них – правильное).

Шаг 2 . Если точка M ( x , y ) вдвое ближе к точке A ( - 1; 0) , чем к линии L x = - 4 , то: ... (Среди вариантов ответа есть ответ |x + 4| = 2д/( x + 1)² + у ² ).

Шаг 3 . Преобразуйте уравнение I x + 4| = 21( x + 1)² + у ² к виду общего уравнения линии второго порядка. (Среди вариантов ответа есть правильный ответ 3 x ² + 4 у ² - 12 = 0 ).

Шаг 4. Уравнение 3x2 + 4у2 -12 = 0 — это уравнение… (Среди вариантов ответа есть ответ «… эллипса»).

Шаг 5 . Получен эллипс с каноническим уравнением… (Среди вариантов ответа есть 22

x -+ У- = 1).

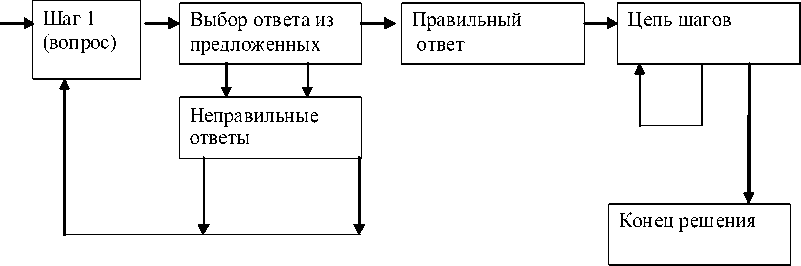
Рис. 2. Блок-схема обучающей программы, работающей в диалоговом режим е (вариант 2: «Учим ся действ овать»)

Система КОРТ (Комплекс Обучения, Репетиций, Тестирования). Контрольнообучающая система КОРТ [8, 9] реализует оба представленных варианта обучающих программ («ищем истину» и «учимся действовать»). Слово «корт» здесь не случайно: главный принцип, положенный в основу этой системы – активный диалог между студентом и компьютером, несколько напоминающий перемещение мяча над теннисным кортом. Система может работать в следующих режимах:

• -    справочные материалы – пользователь имеет возможность получить краткие теоретические сведения по выбранной теме;

• -    обучение – пользователь получает ряд вопросов (заданий) по выбранной теме; за один сеанс можно освоить одну тему, за другой – вторую и т.д.;

• -    репетиция – пользователь получает несколько случайно отобранных вопросов (заданий) из каждой темы, так что выборка охватыва-

• ет материал всей дисциплины или ее достаточно большого раздела; ответы пользователя комментируются, но возврата к вопросу (при любом варианте ответа) нет;

• -    тестирование – отличается от репетиции только тем, что требует обязательной авторизации и не содержит никаких комментариев, за исключением итоговой оценки.

Описанная образовательная технология хорошо вписывается в концепцию интерактивного обучения, содействуя повышению познавательного интереса учащихся. Опыт ее применения в преподавании математических дисциплин подтверждает высказывавшееся ранее мнение [10], что хотя темп обучения в этом случае сугубо индивидуален, в среднем он значительно более высок, чем при самостоятельной работе с «обычной» литературой или при традиционных формах групповых занятий.