Методика построения параметрической 3Д модели червячно-шлицевой фрезы в среде T-Flex CAD

Червячно-шлицевые фрезы применяются для обработки методом обкатки многошлицевых валиков на горизонтальных зубофрезерных станках. Шлицевые валы способны передавать большие крутящие моменты с одной детали на другую. Они широко используются в машиностроении, автомобилестроении, станкостроении, приборостроении и бытовой технике. Проблема заключается в том, что червячные шлицевые фрезы являются специальным инструментом, годным для обработки шлицевых валиков только определённых размеров с заданным числом зубьев. Соответственно необходимо повысить эффективность процесса проектирования данного инструмента. В этом может помочь внедрение параметризации при создании 3Д модели. Это позволит быстро получать готовую модель инструмента в зависимости от требуемых параметров шлицевого вала. Цель данной работы продемонстрировать способ построения 3Д модели чер- вячно-шлицевой фрезы с применением параметризации в среде T-Flex CAD.

Червячная фреза работает по методу обката, что как сказано Радзевичем усложняет проектирование [4, с. 314]. Первым этапом формирования параметрической 3Д модели червячно-шлицевой фрезы является решение задачи профилирования режущей части профиля зуба. Для этого создадим профиль шлицевого вала (рис. 1), в редакторе переменных вводим следующие параметры шлицевого вала: наружный диаметр шлицевого вала d a , внутренний диаметр шлицевого вала d f , диаметр канавок под выход шлифовального круга d 1 , ширину шлица b, фаску шлица f, радиус канавки под выход шлифовального круга r 1 и количество шлицев z. Полученный профиль шлицевого вала выдавливаем при помощи операции «выталкивание» (рис. 2). Длина выталкивания неважна.

Рис. 1. Профиль шлицевого вала

Рис. 2. 3Д профиль шлицевого вала

При помощи команды «параметрический массив» производим обкатку 3Д профиля шлицевого вала (по начальной окружности) по прямой без проскальзывания. Для вычисления диаметра начальной окружности воспользуемся методикой, описанной в справочнике инструментальщика [1, с. 576]. Вводим в редакторе переменных следующие параметры: расчётный наружный                    диаметр da_ras=da_max+2*f_min (где da_max – максимальный наружный диаметр, f_min – минимальное значение размера фаски), расчётный     внутренний     диаметр df_ras=df_min+0,4*E (где df_min – минимальный внутренний диаметр, E – поле допуска на внутренний диаметр), расчётную ширину шлица b_ras=b_min+0,4*E1 (где b_min – минимальная ширина шлица, E1 – поле допуска на ширину шлица), диаметр     начальной     окружности dn=round(sqrt(da_ras^2-0.75*b_ras^2),0.001). Также для применения параметрического массива необходимы значения количества копий n (любое кол-во, главное чтобы образовалось минимум 2 профиля режущей части зуба), номер копии g=0 (при массиве будет осуществляться перебор данного параметра от 0 до n), шаг параметрического массива s (на расстоянии шага будет создаваться n-ая копия массива). Для имитации обкатки 3Д профиля шлицевого вала необходимо математически описать изменение локальной системы координат (ЛСК) 3Д тела от- носительно глобальной системы координат (ГСК) файла. Задаём перемещение уравнением s*g по горизонтальной оси параллельной плоской грани вала (каждая n-ая копия массива будет смещаться по оси на шаг массива относительно предыдущей копии, минус перед уравнением добавляется, если движение необходимо в противоположную сторону направлению оси). Вращение описывается изменением углового положения осей параллельных плоской грани вала относительно положения осей предыдущей n-ой копии массива. Математические уравнения для осей выглядят следующим образом: sin((360*s*g)/(pi*dn)) для одной оси, cos((360*s*g)/(pi*dn)) для другой. Результат параметрического массива представлен на рисунке 4, настройка массива – на рисунке 3. Данный способ заменяет методику, описанную в источнике [2, с. 807].

На плоскости, проходящей через середину параметрического массива, создаем прямоугольный профиль, как показано на рисунке 5. Вводим в редакторе переменных нормальный шаг червячной нарезки Pn0=round((pi*dn)/z, 0.001) [1, с. 576]. выдавливаем полученный профиль симметрично в обе стороны (толщина данного 3Д тела должна быть меньше толщины параметрического массива). При помощи операции «Булева» вычитаем из параллелепипеда параметрический массив, получаем результат, представленный на рисунке 6.

Управляющие параметры Положение

Рис. 3. Настройка параметрического массива

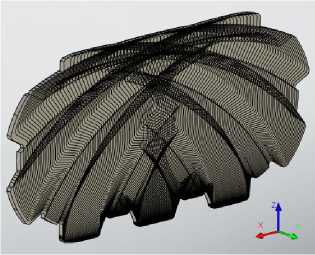
Рис. 4. Результат параметрическо- го массива

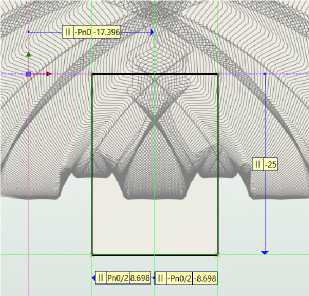
Рис. 5. Построение прямоугольника

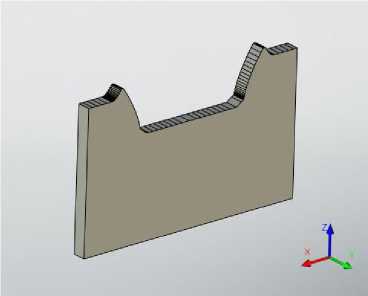
Рис. 6. Результат операции "Булева"

3Д профиль, полученный после булевой операции, уже имеет необходимую геометрию режущей части инструмента, но для дальнейшего моделирования необходим 3Д профиль противоположный полученному. На грани элемента строим впадину между соседними профилями зуба червячно-шлицевой фрезы. Вводим в редактор переменных следующие параметры: hyv высоту головки зуба h=(dn-df_ras)/2, увеличенную высоту головки зуба (высота головки, зуба увеличенная на высоту «усика» hys), высоту профиля зуба после начальной прямой h_x1, высоту фаски профиля зуба hf=1…2 мм, глубину канавки u=1,5…3,0 мм, радиус скругления впадины профиля зуба r=0,5 мм. При помощи введённых параметров рассчитываем полную высоту зуба фрезы h0=round(h+hys+h_x1+hf+u,0.1) [3, с. 493]. Производим построения, приведённые на рисунке 7. Выталкиваем построенный профиль рис. 8. Данный 3Д профиль в дальнейшем моделировании червячношлицевой фрезы будет формировать двойное затылование зуба и червячную нарезку.

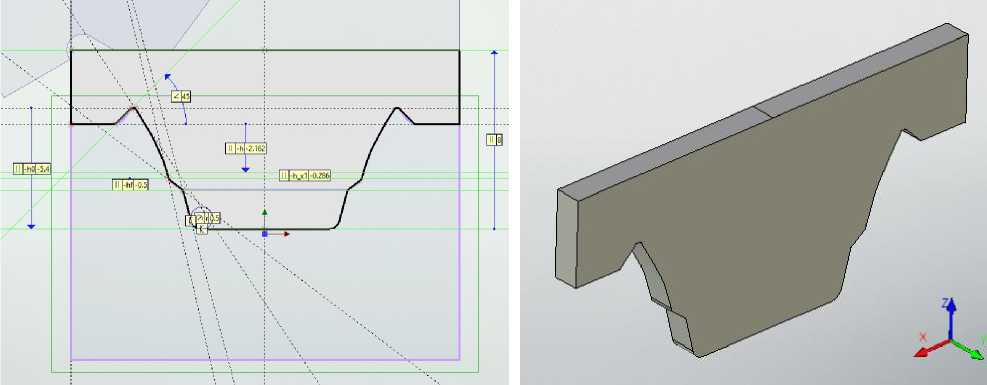
Рис. 7. Построение впадины профиля зуба фрезы

Рис. 8. 3Д профиль впадины профиля зуба фрезы

Следующим этапом построения 3Д модели является создание самой червячношлицевой фрезы. Сформируем продольное сечение тела инструмента. Вводим в редактор переменных следующие параметры: наружный диаметр фрезы da0, длину фрезы L, диаметр посадочного отверстия d, диаметр буртиков d1, длину буртиков l, длина посадочного отверстия до начала «кармана» l2, радиус скругления «кармана» rk, длину фаски буртиков f и длину фаски посадочного отверстия f1. Строим 2Д профиль продольного сечения тела фрезы согласно рис. 9 (для последующей команды «вращение» достаточно половины профиля сечения). Также создаём на оси симметрии инструмента два 3Д узла. Операцией «вращение» поворачиваем получившийся 2Д профиль сечения вокруг оси проходящей через 3Д узлы на 360° (рис. 10).

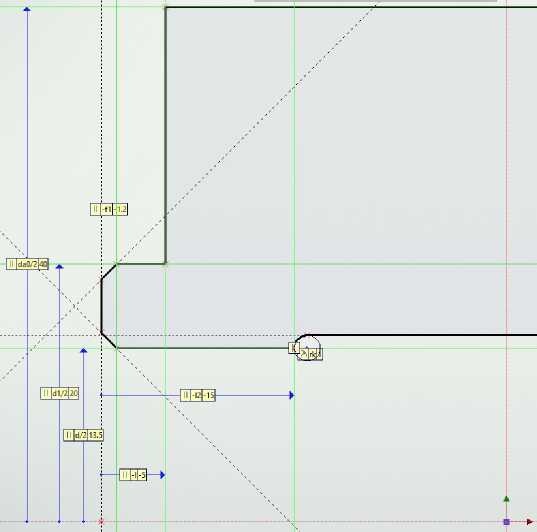
Рис. 9. 2Д профиль продольного сечения фрезы

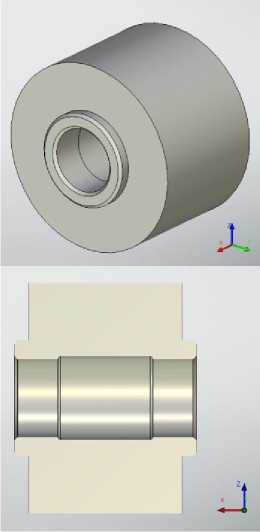
Рис. 10. Начальное формирование тела фрезы

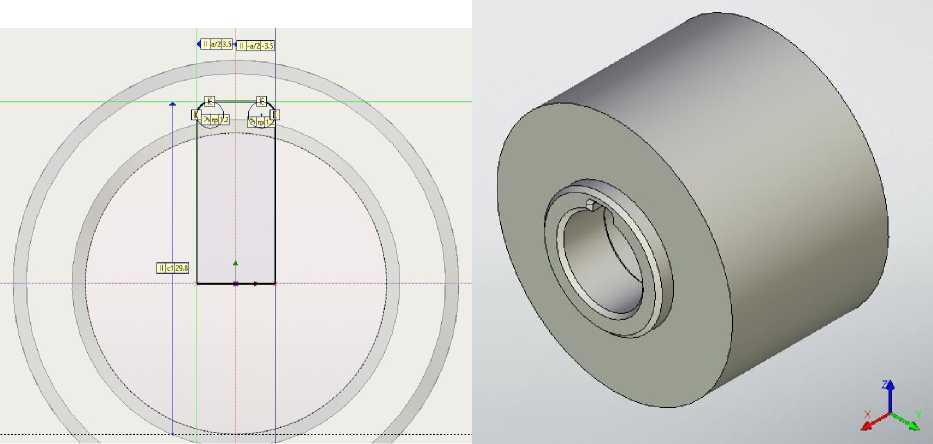
Рис. 11. Профиль шпоночного паза         Рис. 12. Формирование шпоночного паза и фаски на нём

Создаём шпоночный паз. В редакторе переменных вводим его параметры: высоту шпоночного паза c1, ширину шпоночного паза a, радиус скругления шпоночного паза. Профиль паза показан на рисунке 11 в торцовом сечении. Командой «выталкивание» выдавливаем профиль и вычитаем из тела фрезы тело шпоночного паза командой «булева», также формируем фаску на пазе (рис. 12).

Следующим шагом построения 3Д модели является создание винтовых стружечных канавок. На плоскости лежащей на левом торце буртика строим профиль стружечной канавки согласно рисунка 13. Для этого в редактор переменных необходимо ввести следующие параметры: первый     коэффициент     затылования

K=round(pi*da0/z0*tan(alfa_a0),0.1) (alfa_a0 – значение заднего угла при вершине, z0 – число зубьев шлицевого вала, берём из первого этапа построения), второй     коэффициент     затылования

K1=round(1.5*K,1), глубину стружечной канавки hk=round(h0+(K+K1)/2+1,0.1) (h0 – полная высота зуба фрезы, берём из первого этапа построения). Также создаём два 3Д узла (рис. 13). Командой «спираль» вы- талкиваем полученный 2Д профиль. Для этой операции необходимы следующие настройки (рис. 14). Выбираем в окне настроек первую и вторую точки (задание оси), точку начала, в пункте «профиль» ставим параметр «перпендикулярно оси», выбираем контур, первую и вторую точки привязки, в пункте «параметры» выбираем длину и шаг (шаг стружечной канавки Pz0=round(pi*dm0*1/tan(gamma_m0),1);

средний расчётный диаметр dm0=da0-2*h-0.3*K; h – высота головки зуба фрезы, берём из первого этапа построения; угол подъёма винтовой линии фрезы gamma_m0=round(asin(Pn0/(pi*dm0)),0.01); нормальный шаг фрезы Pn0=round((pi*dn)/z,0.001); dn – диаметр начальной окружности шлицевого вала, берём из первого этапа построения; число шлицев z). В пункте «расстояние» выбираем радиус и вычисляем расстояние от оси инструмента до точки начала.

Командой «круговой массив» размножаем тело винтовой стружечной канавки фрезы вокруг оси инструмента с числом копий равному числу зубьев фрезы z0 (рис. 15). Из тела фрезы командой «булева» вычитаем круговой массив (рис. 16).

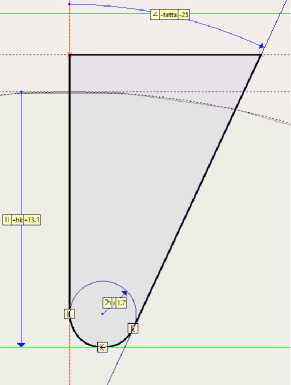
Рис. 13. Профиль стружечной канавки

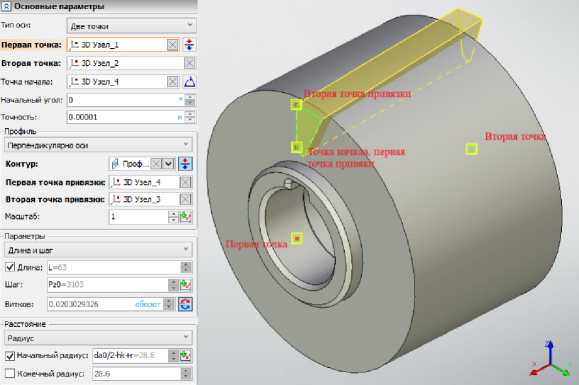
Рис. 14. Настройка команды "спираль"

Рис. 15. Круговой массив

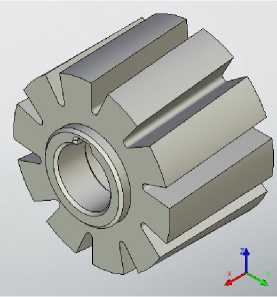
Рис. 16. Формирование винтовых стружеч- ных канавок

Для удобства задания положения результата задачи профилирования режущей части профиля создадим локальную систему координат ЛСК. Расположение ЛСК задаём на пересечении вертикальной оси симметрии с горизонталью, проходящей через вершину «усика» (рис. 17). Командой «3Д фрагмент» вставляем 3Д профиль в файл с червячно-шлицевой фрезой. Сов- местив ЛСК 3Д профиля вершиной стружечной канавки, необходимо произвести поворот 3Д профиля вокруг оси Z на величину угла подъёма винтовой линии фрезы gamma_m0, тем самым расположив его касательно к поверхности стружечной канаки. Задание положения показано на рис. 18.

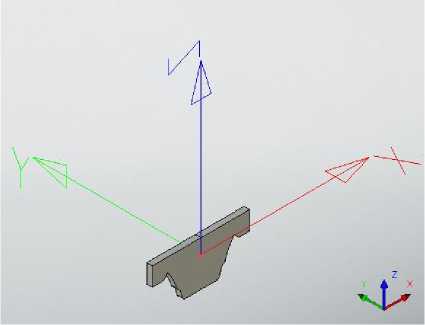
Рис. 17. Создание ЛСК

Рис. 18. Задание положения 3Д профиля

Командой «линейный массив» копируем 3Д профиль по оси, перпендикулярной горизонтальной плоскости, на расстояние (K1-K)/2, это необходимо для формирования второго затылка (рис. 19). Полученным первому и второму 3Д профилям нужно задать траекторию червячной нарезки (получается суммарным смещением по двум осям в горизонтальной плоскости) и траекторию спада затылка (получается смещением по оси, перпендикулярной горизонтальной плоскости). Описанные выше траектории червячной нарезки и по спаду затылка суммарно создают одну общую траекторию. Также на протяжении всей траектории необходимо, чтобы 3Д профиль поворачивался за счёт изменения углового положения двух осей, перпендикулярных горизонтальной продольной оси фрезы, относительно предыдущего своего положения. В редактор переменных вводим количество копий n и номер копии g=1. Командой «по параметрам» осуществим описанное выше. Траектория червя-ной нарезки математически описывается следующим образом: по продольной горизонтальной оси фрезы ((g-1)/n)*(Pn0/z0)

(одинаково для первого и второго 3Д профилей), по поперечной горизонтальной оси ((g-1) *K/n)*cos((360/z0)*((g-1)/n)) (для первого 3Д профиля) и ((g-1) *K1/n)*cos((360/z0)*((g-1)/n)) (для второго 3Д профиля). Траектория спада затылка математически описывается следующим образом: по оси перпендикулярной к горизонтальной плоскости -((g-1)*K/n)*sin((360/z0)*((g-1)/n)) (для первого 3Д профиля) и -((g-1)*K1/n)*sin((360/z0)*((g-1)/n)) (для второго 3Д профиля). Поворачивание 3Д профилей вокруг горизонтальной продольной оси фрезы математически описывается следующим образом: изменение углового положения горизонтальной поперечной оси cos((360/z0)*((g-1)/n)) (одинаково для первого и второго 3Д профилей) и изменение углового положения оси, перпендикулярной горизонтальной плоскости, sin((360/z0)*((g-1)/n)) (одинаково для первого и второго 3Д профилей). Настройка операции «по параметрам» показана на рисунке 20. Результат операции показан на рисунке 21.

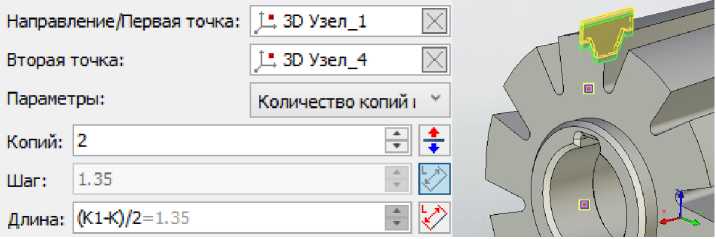
Рис. 19. Создание второго 3Д профиля операцией "линейный массив"

Положение

X: | ((g-1)/n)"(Pn0/z0]=0

Y: | ((g-1)"K/n)"cos((360/z0=(

Z: | -((g-1)'K/n)'sin((360/z0)H

Направление оси Y

• X: |p

• Y: | cos((360/z0)"((g-1)/n))=1

Z: | 3jn((360/z0)-((g-1)/n))=0

Положение

X: | ((g-1)/n)"(Pn0/z0]=0

• Y: | ((g-1)"K1/n)"cos((360/z=(

Z: | -((g-1)'K1/n)'sin((360/z-=C

Направление оси Y

• X: |p

• Y: | cos((360/z0)-((g-1)/n))=1

Z: | sin((360/z0)"((g-1)/n))=0

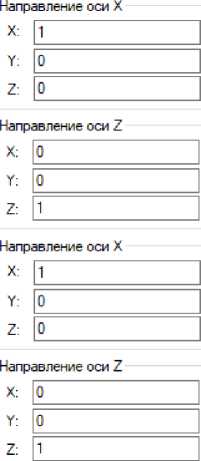
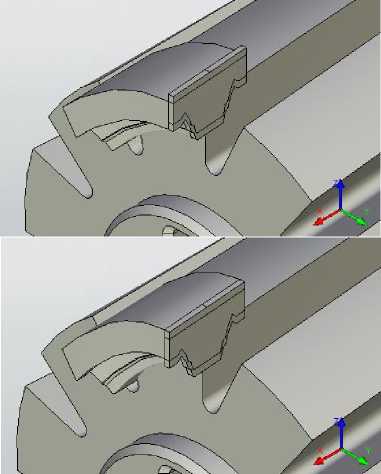
Рис. 21. Результаты первой и второй операций "по параметрам"

Рис. 20. Настройка для первой и второй операций "по параметрам"

Полученные два тела «по параметрам» необходимо размножить по всей длине инструмента по траектории червячной нарезки. Движение вдоль продольной горизонтальной оси математически задаётся -g1/z0*Pn0, а круговое движение вокруг продольной горизонтальной оси изменением углового положения осей, лежащих в одной плоскости и перпендикулярных продольной горизонтальной оси, относи- тельно предыдущего положения математически задаётся для горизонтальной поперечной оси sin((360/z0*g1)-(360*(g1/ z0*Pn0)/Pz0)), а вертикальной cos((360/z0*g1)-(360*(g1/z0* Pn0)/Pz0)) (n1 – количество копий параметрического массива, g1=1 – номер копии параметрического массива). Настройка операции «параметрический массив» показана на рисунке 22, а результат на рисунке 23.

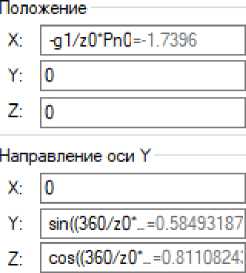
Рис. 22. Настройка операции "параметрический массив"

Рис. 23. Результат операции "па- раметрический массив"

Последним шагом построения 3Д модели червячно-шлицевой фрезы является вычитание из тела фрезы параметрического массива (рис. 24).

Рис. 24. Червячно-шлицевая фреза

Благодаря данной методике и другим способам, например, один из них описан статье Хейфеца [5, с. 47]. 3Д моделирования червячно-шлицевой фрезы можно быстро получать инструмент других размеров под конкретные размеры шлицевых валов, таким образом повышается эффективность проектирования. Также по данной 3Д модели можно получить чертёж (рис. 25), который будет обновляться в со- ответствии с изменением параметров фрезы, что также повышает эффективность получения конструкторской документации. Дальнейшее развитие CAD систем позволит ещё больше упрощать проектирование различных изделий и вполне возможно приведёт к полной автоматизации производственных процессов без участия человека.

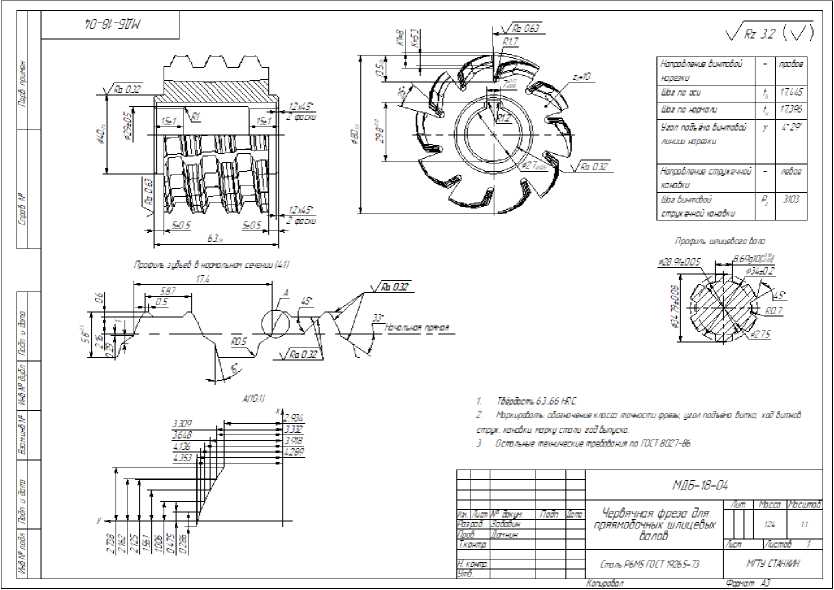
Рис. 25. Параметрический чертёж червячно-шлицевой фрезы