Методология оценки и анализа характеристик точности мехатронных манипуляторов по кинематическим моделям

Точностные показатели (ТП) мехатронных манипуляторов (ММ), простота их математических моделей и их последующего программирования во многом определяет их эксплуатационные возможности. При аналитическом программировании ММ реализация их движений осуществляется на основе получения и обработки информации из базы данных, характе- ризующих математическую модель ММ и рабочей (оперативной) среды, а также ее состояния, фиксируемого показаниями сенсоров.

Разработке и апробации математических моделей точностного анализа ММ посвящено много работ. В [1] дан их обзор, в частности сюда относятся работы авторов, где представлены кинематические точностные модели.

Обычно задачи геометрического точностного синтеза решаются после выбора рациональной для поставленной задачи схемы механизма и после завершения кинематического точностного синтеза, который производится на основе теоретических исследований, относящихся к геометрическому точностному синтезу, так как эти два вида точностного синтеза взаимосвязаны. Это обусловлено тем, что уже в процессе кинематического синтеза при оценке точностных возможностей механизмов производится часть расчетов, позволяющих ориентировочно оценить оптимальные значения параметров или выявить ограничения, накладываемые на них, а на стадии геометрического синтеза уточняются эти оптимальные значения параметров, дающие приемлемые значения теоретической ошибки.

Решение задачи синтеза направлено на создание структуры механизма и расчет его параметров. Поэтому различают два вида задач синтеза: структурный и параметрический.

В зависимости от оценочной функции задачи синтеза можно разбить на задачи кинематического, динамического, прочностного синтеза и задачи синтеза из условий технологии производства всего механизма, что означает определение рациональных параметров и разработку требований к точности его составных частей: узлов и деталей, - прямая задача.

Далее на основе разработанных чертежей и допусков на изготовление и сборку узлов и деталей механизма вычисляется выходная точность механизма, - обратная задача.

Многие параметры, с которыми сталкивается конструктор при точностном синтезе, являются случайными величинами (функциями). Наличие случайных отклонений должно учитываться при синтезе допусков на конструктивные параметры и ведет к необходимости статистического анализа механизма в целом и к оценке отдельных ошибок.

Задачи точностного синтеза могут относиться как к кинематике, так и к динамике. Основными задачами, решаемыми в точностном синтезе, являются:

• -    в кинематическом точностном синтезе - выбор и создание кинематической схемы механизма, наиболее близко соответствующей заданной функции;

• -    в геометрическом точностном синтезе - расчет величин параметров механизма для минимизации его теоретической ошибки. Минимизация может производиться в зависимости от характера допустимой теоретической ошибки, например, по методу наилучшего (равномерного) приближения, квадратичного приближения или интерполирования.

Кинематический синтез - выбор кинематической схемы механизма для обеспечения требуемого вида и закона движения.

Динамический синтез - выбор динамических характеристик для обеспечения динамической точности ММ.

Прочностной синтез - разработка конструктивных форм механизма, обеспечивающих его прочность, долговечность.

Синтез из условий технологии производства связан с разработкой технологических и технико-экономических показателей проектируемого механизма, определяемых эксплуатацией, ремонтом, производством. Ими могут быть величины допусков на изготовление деталей звеньев, условия сборки и т.д.

По материалам Японской ассоциации промышленной робототехники из 23 показателей робототехники [2] по степени важности первые 7 позиций занимают следующие направления разработок по порядку (табл. 1). Из этой таблицы видно, что проблема повышения ТП ММ является одной из приоритетных.

Табл. 1

Место по степени важности	Направление и цели исследований
1	Повышение быстродействия роботов
2	Повышение точности позиционирования
3	Уменьшение габаритов роботов
4	Методы управления от ЭВМ
5	Снижение стоимости
6	Очувствление
7	Модульность (взаимозаменяемость)

Погрешности мехатронных манипуляторов и задачи их анализа

Теоретический анализ погрешностей ММ обычно осуществляется по видам, на основе принятой классификации. Как правило, определяющими считаются два классификационных признака:

• -    признак связи тех или иных составляющих погрешностей с первичными факторами (например, зазорами в кинематических парах, упругостью звеньев манипулятора, погрешностями базирования самого манипулятора или объекта производства относительно него и т.д.);

• -    признак, характеризующий проявление составляющих погрешностей (они могут быть постоянными или переменными во времени, систематическими или случайными).

Погрешности позиционирования ММ образуют векторное поле, корректное описание свойств которого позволяет вынести объективное суждение о точности.

Первичные погрешности всегда являются неопределенными и для описания этой неопределенности применяют различные модели, основные из которых [3]: задание погрешностей интервалами допустимых изменений со строго ограниченными известными предельными значениями. Здесь возможны как детерминированные, так и вероятностные модели описания.

В обоих типах моделей области неопределенности задаются эллипсоидами. В первом случае эллипсоид представляет результат аппроксимации реальной, более сложной по форме области неопределенности. Во втором случае эллипсоиды представляют собой поверхности равных значений плотностей вероятности при распределении Гаусса. Алгоритмы вычислений точностных показателей как в детерминированной, так и в вероятностной моделях и их взаимосвязь приведены в работе [3].

Физические и технические причины появления погрешностей в связи с первичными факторами подробно обсуждались в монографии [4].

Влияющие факторы

На погрешности отработки траектории рабочего органа ММ и на их точностные показатели влияют следующие основные факторы:

• 1.    Кинематическая схема механизма манипулятора.

• 2.    Соотношение длин звеньев механизма.

• 3.    Способ компоновки двигателей в механизм манипулятора и т.д.

• 4.    Коэффициенты динамических ошибок приводов и их различие по степеням подвижности.

• 5.    Геометрия и кинематика программных траекторий и законов движения, а именно:

• -    вид траектории;

• -    место программной траектории в рабочей зоне, размеры рассматриваемого отрезка траектории, положение крайних точек траектории в рабочей зоне.

Роль и относительная значимость перечисленных факторов могут изменяться в широких пределах. В дальнейшем основным фактором считается вид кинематической схемы, количественные результаты будут относиться преимущественно к ММ с антропоморфной кинематической схемой.

Для схем манипуляторов с поворотными двигателями угловые относи -тельные перемещения выходных звеньев естественно принять за обобщенные координаты механизма манипулятора, как на рис. 1а. Преобразование изменений линейных и угловых координат рабочего органа в перемещения выходных звеньев приводов является одноэтапным, простым и однозначным.

Для схем манипуляторов со структурной избыточностью, т.е. с «лишними» степенями подвижности, как на рис. 1 б, преобразование линейных и угловых координат рабочего органа к обобщенным координатам механизма уже не является однозначным, известны исходные соображения относительно того, как целесообразно распоряжаться лишними степенями свободы. В приведённых выше примерах механизмы плоские, но все качественные положения в равной степени относятся также и к пространственным механизмам.

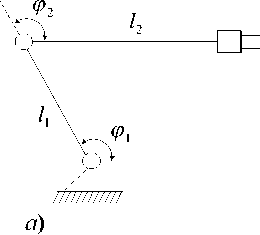
Рис. 1. Мехатронные манипуляторы с поворотными двигателями а ) без двигательной избыточности б) с двигательной избыточностью

Методология точностного анализа мехатронных манипуляторов При расчёте ТП ММ эффективны аналитические методы исследования [1].

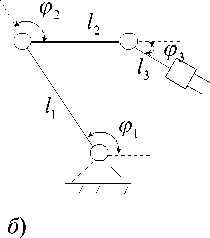
Номинальное положение полюса С схвата ММ определяется зависимостью для базовой плоскости ММ r = r *( q),                              (1)

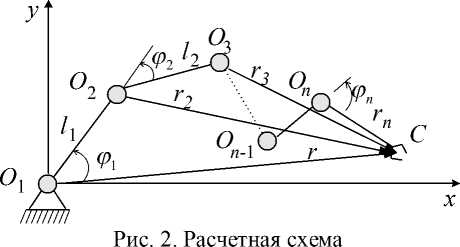
где q = [ q 1 , q ₂ ,..., q ₂ n ] T - вектор-столбец обобщенных координат, которыми являются длины l i звеньев, межзвенные углы a i , i= 1,2,..., n (рис. 2).

Рассматривая значения ошибок ^q i в шарнирах O i для конфигураций '                                              ''

q е Q = {qi < qi > qj},

можно оценить точность ММ.

Погрешность позиционирования (ПП) ММ в точке r будет:

, А * д r * ,

А = A r * =--- A q = A ( q , r ) A q = A A q .

∂ q

При оценке ПП следует пользоваться скаляром:

А ² = |A r |² = A q^TA T A A q = q T Ф A q .                 (2)

Анализ точности сводится к задаче квадратичного программирования в области задания A q eA Q . При детерминированном анализе области задания первичных ошибок Aq могут быть представлены в виде: параллелепипеда A Q = { A q : S’ * <  S i <  §”, i = 1,2,..., n }; эллипсоида A q^TR A q = 1, где R - диагональная матрица предельных допусков на A q .

Однако могут быть ошибки и случайного характера, например, проявляющие себя при многократном повторении операции позиционирования в какой-либо точке рабочей зоны. В последнем случае задается плотность распределения погрешности в каждом шарнире f(A ф _i), где i =1,2,.,n, и затем определяется плотность распределения ПП f( A r)=f(Ax, A y, A z).

Компоненты вектора смещения A = A r полюса захвата имеют совместную плотность распределения:

f ( A r ) = f ( A x , A y , A z ) = (2 n ) ^{- 3/2} | K |^4/2 exp( - 0,5 A ^TK -’A ), где K - корреляционная матрица размером 3х3 системы случайных величин A x, A y, A z; ее диагональные элементы - это их дисперсии, внедиагональные - корреляционные моменты их парных комбинаций, ее след S p llKII=D_r=D_x+D_y+D_z характеризует всенаправленную теоретическую повторяемость.

Стоящая под знаком экспоненты квадратичная форма от Δ x, Δ y, Δ z принимает постоянные значения на поверхности некоторого эллипсоида, характеризующего форму и размеры окрестности номинального позиционирования, куда с некоторой фиксированной вероятностью р попадает захват ММ.

Определение формы и ориентации эллипсоида равных вероятностей (э.р.в) сводится к построению матрицы К , нахождению ее собственных чисел и собственных осей. При нормальном законе распределения и независимости ошибок A q i погрешность A r распределена по нормальному закону, причем поверхности равной вероятности имеют форму эллипсоида. Скалярными оценками ТП могут служить их дисперсии или величина большой полуоси эллипсоида при заданной доверительной вероятности.

Новым для мехатроники является такое представление результатов расчетов, при котором каждой точке рабочей зоны приписывается два параметра: размеры наибольшей и наименьшей осей эллипса или эллипсоида, определяемые как наибольшее и наименьшее собственные значения соответствующих квадратных матриц. Каждый раз определяя направления наибольших и наименьших погрешностей, можно построить непрерывные кривые, касательные к которым определяют направления наибольших и наименьших погрешностей, называемых главными линиями точности (ГЛТ). Главные линии точности - это линии, в каждой точке которых направление касательных к ним совпадают с направлением смещения захвата, в котором ПП экстремально изменяется. В пространстве через каждую точку рабочей зоны ММ можно провести три ГЛТ, ортогональных относительно друг друга в этой точке.

Для иллюстрации построения ГЛТ в работе [4] представлена ММ в базовой плоскости (рис. 3). Соотношение (1) примет вид (см. рис.2):

x

y

n

Е vcos Pi i=1

n

Е lr ^sin P i

. i = 1

n

Матрица в соотношении (2) Ф={ фу}, i,j = 1,2,^,n, имеет компоненты [1]: nn фsp=ЕЕlljcos(Pi -Pj) приs,p=n;

i = s ^j = p

n фsp =E l sin( Pl - Pj) при p>n. i=s

По уравнению |Ф-ХЯ|=0 вычисляются экстремальные смещения по направлению tgy* = —, i =1, 2, и величине. Вводя полярную систему коор-Ax динат (г,у), из Ay=rAy, Ax Аг (рис. 3) вычисляют уравнения ГЛТ:

tg Y ⁽ i )

Р

r

V-Vо=|

^г 0

d р , или r = r( у , у ₀ ).

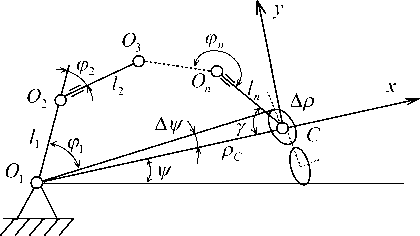
Рис. 3. Схема для расчета ГЛТ

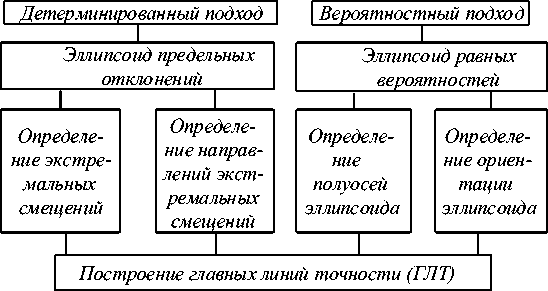
Рис.4. Алгоритм вычислений ТП мм в детерминированной и вероятностной постановке

На рис. 4 представлены алгоритмы построения ГЛТ в детерминированной и вероятностной трактовках.

В [3] показано, что анализ точности MM вероятностным и детерминированным методами с введением индексов оценки ТП даёт качественное совпадение. Например, сравнение результатов вычислений главных смещений полюса схвата (метода кинематических осей и метода эллипсоида рассеяния) показывает их сходство, если в матрице R за компоненту 5 q_i взять значения дисперсий первичных погрешностей D i [1].

На рис. 5 приведены базовые кинематические схемы типовых компоновок ММ.

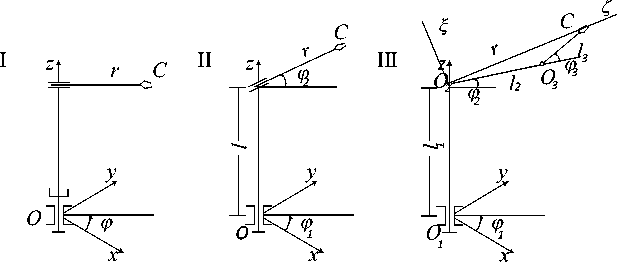
Рис. 5. Базовые схемы типовых компоновок

Обобщенные координаты соответственно будут:

q I = [ r ф z ] т , q II = [ r Ф 1 Ф 2 ] т , q III = [ ф 1 Ф 2 ф 3 ] ^т .

ГЛТ ММ cо схемой I и II совпадают с линиями координатной сетки, тогда как у ПР с антропоморфной схемой III ГЛТ имеют более сложный характер зависимости местоположений главных смещений [3].

Главные смещения рассчитываются по формуле A r ( ¹) = A A q ( ¹) . Согласно алгоритму рис. 3 имеем из определителя типа |Ф - A R | = 0 собственные числа A i = 1, 2, 3, определяющие модули главных смещений A r i :

∆ r I ⁽¹⁾ = λ 1 = δ r ; ∆ r I⁽I²⁾ = λ 2 = r δ φ ; ∆ r I⁽II³⁾ = λ 3 = δ z ;

Для схемы II главные смещения составляют:

∆ r _I ⁽ _I ¹⁾ = δ _r ; ∆ r _I ⁽ _I ²⁾ = ( r cos ϕ ₂ ) δ_{ϕ 1}; ∆ r _I ⁽ _I ²⁾ = r δ_{ϕ 2};

Для схемы III имеем:

∆ r _I ⁽ _II ¹⁾ = [ l ₂cos ϕ ₂ + l ₃cos( ϕ ₂ + ϕ ₃)] δϕ ₁;

∆ r _I ( _II ,) = 0,5( r ² δ ϕ ² + l 3 ² δ ϕ ² ± J ( r ² δ ² - l ² δ ²) + ( r ² - l ² + l ²) δ ² δ ²) .

III                ϕ ₂    3 ϕ ₃          ϕ ₂    2 ϕ ₃            23 ϕ ₂ ϕ ₃

В полярных координатах r и ϕ с началом в точке О2 (шарнир второго звена) и обозначив через γj (j = 2, 3) угол между направлениями ∆rI(II2,3) и r, получим:

tg γ (2,3)

λ 2,3 ( r ² - l 2 ² + l 3 ²)

( λ 2,3 - r ² δ φ ²₂) [( l ₂ + l ₃)² - r ²][ r ² - ( l ₂ - l ₃)²

Введя дополнительно систему координат хО2у и используя соотношения ∆х = r, ∆y = r∆ϕ, путем интегрирования зависимости tgγ(2,3)dr = rdφ строят ГЛТ.

Для ММ мод. ТУР-10 ГЛТ в базовой плоскости приведены на рис. 6.

Для расчета взяты исходные данные из паспорта ПР мод. ТУР-10:

l 1 = 0,5 м, l 2 = 0,67 м,

δ ₁ = 2,3 ′= 6,69 ⋅ 10 ^{- 4},

δ ₂ = 1,4 ′= 4,07 ⋅ 10 ^{- 4}, δ ₃ = 2,2 ′= 6,4 ⋅ 10 ^{- 4}.

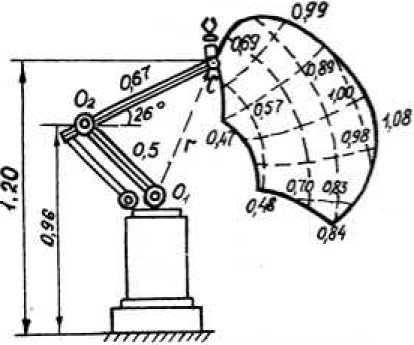
Рис. 6. Главные линии точности мехатронного манипулятора модели ТУР-10

Подобные ММ находят широкое применение, например, такие модели, как ТУР-10 (Россия) (рис. 6), Unimate 7060, Unimate 6645 фирмы Kawasaki (Япония); IRB-160, IRB-6 фирмы ASEA (Швеция) и др.

При проектировании подобных ММ существенное значение имеет выбор как геометрических параметров (соотношений длин звеньев; углов взаимного разворота звеньев, а также местоположений схвата в рабочей зоне ММ), так и конструктивно-технологических параметров (тип и характеристики привода, системы управления, допусков на изготовление элементов и узлов MМ.

Заключение

Для каждой точки рабочей зоны ММ существует свой индекс точности, который зависит от конфигурации руки. И если при выполнении какого-либо операционного движения рука ММ может принимать две или больше конфигураций, то можно из них выбирать ту опорную конфигурацию, которая даёт лучшие ТП [3].

Кроме этого могут быть выявлены оптимальные в смысле точности области рабочей зоны ПР, оптимальные конфигурации руки для отдельных её областей [3, 4], а также может быть выбрано оптимальное соотношение длин звеньев руки для данного положения схвата и найдены оптимальные допуски на параметры руки и привода [1].

Предъявленная методология комплексной оценки и анализа ТП ММ по кинематическим точностным моделям представляет собой эффективный арсенал расчётных инструментов как для разработчиков, так и пользователей подобных средств автоматизации, поскольку здесь устанавливаются аналитические взаимосвязи между «метрикой», допусками на функциональные и конструктивные компоненты модулей, конфигурации руки, характера структурной избыточности и выходным ТП ММ.