Методы и алгоритмы решения комплексной задачи компоновки

Необходимым условием развития экономики страны является качественное развитие промышленных объектов. В современных условиях проектирование промышленных объектов должно обеспечивать получение оптимальных проектных решений по ряду критериев. От оптимальности принятых проектных решений зависит эффект от внедрения промышленного объекта. Одним из основных этапов в конструкторском проектировании является этап топологического синтеза, заключающийся в получении пространственной модели проектируемого объекта. Пространственная модель будущего промышленного объекта включает строительные конструкции, размещенное оборудование, сеть технологических соединений, вспомогательное оборудование и металлоконструкции.

Объекты и методы исследований

Этап структурного синтеза в конструкторском проектировании промышленных объектов имеет большое значение, так как решения, принятые на этом этапе, во многом определяют стоимость промышленного объекта и эффективность его эксплуатации впоследствии. Проектирование структуры промышленного объекта всегда связано с выполнением требований различных отраслевых стандартов, ведомственных инструкций и других требований различного характера. Например, по требованиям безопасности между аппа- ратами с высокой температурой среды в них и трубопроводами высокого давления должно выдерживаться минимально допустимое расстояние. Также целесообразно, с точки зрения взаимозаменяемости и удобства обслуживания оборудования, группировать однотипное оборудование. Другие ограничения связаны с конструктивными особенностями производственных помещений.

Например, ограничение максимальной массы оборудования, располагаемого на верхних этажах, или ограничение максимальных габаритных размеров оборудования. Также возможно использование ограничений, основанных на опыте конструктора, которые позволяют, например, упростить монтаж оборудования при модернизации производства. Существует множество таких ограничений: конструкционные ограничения, технологические ограничения, ограничения, связанные с охраной труда, ограничения, связанные с удобством последующей эксплуатации объекта и т.д. Поэтому на стадии разработки математической модели для решения задачи компоновки промышленных объектов необходимо учесть весь набор ограничений, так как они напрямую влияют на качество получаемого решения. Однако, специфика предметной области для каждой конкретной практической задачи, а также возможность наложения дополнительных ограничений делает задачу учета всех ограничений нереализуемой на практике. Решением данной задачи является разработка метода формирования и контроля системы ограничений. Необходимо разработать метод задания ограничений различного характера.

Примем допущение, ограничения, связанные с проведением дополнительных расчетов (гидродинамические, термодинамические и т.д.) рассматриваются в общем виде. Результат расчетов является неким отображением свойств вершин и ребер гиперграфа и подграфа.

Рассмотрим ограничения математической модели. Все ограничения при компоновке промышленных объектов рассматриваются как правила вида «Если А, то В». Правила отражают зависимость свойств объектов, областей размещения и технологических соединений в соответствии с приведенной классификацией. При этом правила формируются на основе информации, полученной от эксперта в данной предметной области. Эксперт формирует представление о решаемой задаче в виде совокупности правил и данных. Данные в этом случае представляют собой значения свойств объектов. Правила являются ограничениями компоновки и определяют способы преобразования данных при решении задачи. На начальном этапе эта информация носит обобщенный, неструктурированный характер. Структурирование и запись правил в формализованном виде производит непосредственно разработчик проекта, который также может являться экспертом при решении задачи. Формализация правил и формирование системы ограничений производятся в порядке, приведенном в данной процедуре.

Рассмотрим порядок формирования системы ограничений в формализованном виде (рис. 1). Данный подход одинаков для всех ограничений, кроме требующих проведения специальных расчетов. Задание таких ограничений имеет некоторые отличия, которые будут рассмотрены отдельно.

Для каждого ограничения математической модели решаемой задачи определяется тип в соответствии с приведенной классификацией. Например, ограничение «размещение однотипных аппаратов в одном помещении» относится к типу 1

Экспертная информация

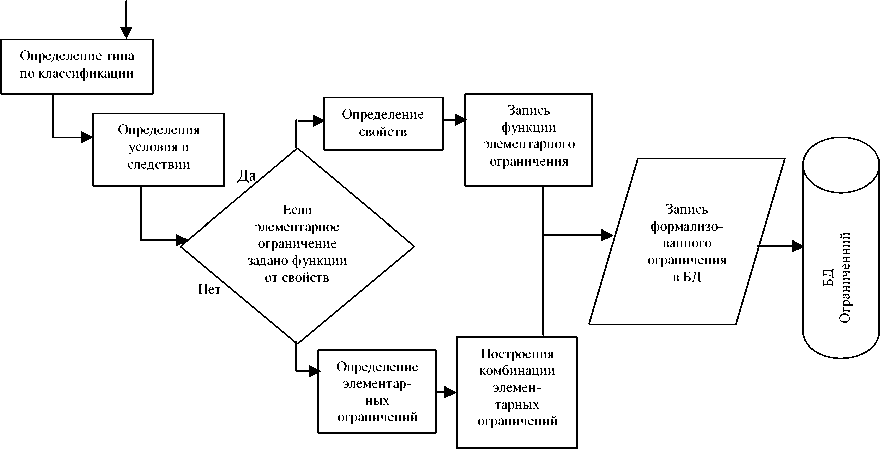
Рисунок 1 - Блок-схема процедуры формирования ограничений

Далее ограничение записывается в виде правила. Для этого определяется условие и следствие. В рассматриваемом примере условием будет являться следующее: «тип размещаемого аппарата равен типу уже размещенного в помещении». А следствием является «аппарат необходимо размещать в том же помещении». Так ограничение в виде правила будет записано следующим образом: «Если тип размещаемого аппарата равен типу уже размещенного в помещении, то аппарат необходимо размещать в том же помещении».

Затем выделяются элементарные ограничения, соответствующие условию и следствию. Если условие содержит комбинацию ограничений, то сначала выделяются элементарные ограничения. Пусть в данном примере для свойства «тип» его номер zls^l^tSs,^]^ &u_m.

• x, e u_m

После того, как формализованы условие и следствие правила, оно записывается в виде «Если А, то В». В данном примере правило примет вид

Ecituz\s.,x l = zr5.,j ДИх. ем .mox eu .

Описанная процедура проводится для каждого ограничения в решаемой задаче.

Для определения некоторых условий необходимы специальные расчеты.

Например, гидродинамические расчеты для определения максимальной длины трубопровода. Тогда запишем ограничение в общем виде

Если f (z,,z2,..,z„ )©Zy,то В, где: У (ZM Z2>ee»ZM - функция, зависящая от значений свойств вершин и ребер;

z z z

• - значения свойств;

zi - ограничение значения функции.

Формирование ограничений в данном случае будет выполняться следующим образом. Ограничение также классифицируется по приведенной классификации. Далее аналогично выбирается условие и следствие правила.

Затем выбираются свойства, от которых зависит значение рассчитываемого показателя. Для данного примера это количество точек изменения направления трубопровода, диаметр и давление на входе. Эти свойства являются переменными для функции расчета. Правило включается в систему, при этом, функция записывается как обращение к некоторой предопределенной функции.

Набор функций процедур (функций специализированного расчета) определяется заранее. Это сужает область применения данного подхода при решении задач на практике с применением ЭВМ. Но применение библиотек расчетов позволяет применять подход в различных предметных областях.

Совокупность всех правил, заданных в соответствии с приведенной процедурой в виде, составляет систему ограничений модели при решении задачи компоновки промышленных объектов.

Результаты и их обсуждение

Разработана обобщенная структура математической модели компоновки промышленных объектов, основанная на применении N-ориентированных гиперграфов для моделирования структуры технической системы и позволяющая формализовать запись ограничений, заданных в виде экспертной информации, через ограничения значений свойств объектов, областей размещения, технологических соединений.

Выводы

В результате исследования разработан подход к математическому моделированию компоновки промышленных объектов, основанный на применении N-ориентированных гиперграфов для описания структуры технической системы, методах и алгоритмах автоматизированного формирования ограничений моделей и их учета при решении задач компоновки. Данный подход применим для решения круга задач компоновки промышленных объектов, таких как объекты химического производства, машиностроения, пищевой и легкой промышленности, в цехах как ангарного, так и многоэтажного типа. Также с применением данного подхода возможно решение задачи компоновки промышленного объекта, состоящего из нескольких цехов.