Методы математической статистики в педагогических исследованиях: теория и практика применения

УДК 796.6

В научно-педагогических исследованиях с целью доказательства эффективности экспериментальной работы, активно применяются методы математической статистики.

Ранее данные методы в основном использовались в психологии. Общеизвестно, что статистика – это основанное на вероятности моделирование и логический вы- вод. 1880-е годы – начало использования современной статистики в психологии благодаря исследованиям Г. Фехнера (психофизика). Статистические методы обработки астрономических наблюдений развивались во второй половине XVIII века, и в начале XIX века они были согласованы с математической теорией вероятности. Одними из ключевых фигур во всем этом были ученые П. С. Лаплас и К. Ф. Гаусс.

В настоящее время используются такие методы математической статистики: описательная статистика и теория статистического вывода. Немецкий дидакт Л. Клинберг считает, что только с помощью данных методов можно доказать результаты проведенной работы [4, с. 181–182.]. Цитируем слова российского ученого, доктора педагогических наук, профессора, заслуженного деятеля науки Российской Федерации Загвязинского В. И.: «Статистические методы являются базовым инструментарием обработки данных измерений практически во всех областях научного знания. Наиболее широкое применение они получили в естественных науках, где возникла острая необходимость анализа огромного массива эмпирических данных. В сочетании с методами планирования и моделирования эксперимента статистические методы позволяют выявлять объективные закономерности при проверке различных научных гипотез» [3].

Статистические данные могут передаваться на разных уровнях, начиная от нечислового дескриптора (номинальный уровень) до числового в отношении нулевой точки (уровень отношения).

Для сбора статистических данных можно использовать ряд методов выборки, включая простую случайную, систематическую, стратифицированную или кластерную выборку.

При анализе данных используются два типа статистических методов – описательные и статистические. Описательные методы позволяют нам описать данные так, чтобы не было необходимости в их анализе. Они могут быть использованы для того, чтобы определить, есть ли в данных какая-нибудь аномалия; например, что некоторые характеристики выше или ниже среднего, или что характеристики не соответствуют некоторой тенденции, которая может быть предсказана. Это позволяет нам говорить о том, как выглядят данные.

Давно известно, что знание статистики необходимо при решении определенных типов научных задач [13], а понимание статистики является важной частью навыков интерпретирования результатов проверяемой гипотезы [12].С этой целью в Московском государственном институте культуры для аспирантов второго курса авторами данной статьи была разработана специальная дисциплина «Методы математической статистики в педагогическом исследовании». В рамках изучения данной дисциплины аспиранты обучаются применять методы математической статистики в своих исследованиях, в том числе с помощью современных компьютерных программ.

Главной задачей данного курса является – научить аспирантов использовать методы математической статистики для проверки правильности гипотезы.

Для решения данной задачи мы предлагаем освоить критерии Фишера и Стьюдента для проверки равенства дисперсий и средних нормальных генеральных совокупностей; критерий Манна-Уитни; критерий знаковых ранговых сумм Уилкоксона; критерий Колмогорова-Смирнова для проверки нормальности распределения.

Для достоверной проверки своих результатов эксперимента рекомендуется использовать все доступные технологии, чтобы помочь лучше понять и статистически доказать предоставленные данные [11].

Для удобного применения методов математической статистики в век инновационных технологий рекомендуем использовать программу SPSS statistics (с английского Statistical Package for the Social Sciences – статистический пакет для общественных наук), которая «занимает ведущее положение среди программ, предназначенных для статистической обработки информации» [5].

Важно также научить аспирантов верно интерпретировать полученную информацию, критически оценивать, делать те или иные выводы на основе представленных статистических результатов и оформлять результаты в графическом или табличном виде [14].

Разберем конкретный пример применения методов математической статистики в педагогическом исследовании.

№	Уровень интеллекта поСтенфорду-Бине	№	Уровень интеллекта поСтенфорду-Бине
1.	116	16.	119
2.	121	17.	113
3.	116	18.	107
4.	111	19.	109
5.	114	20.	109
6.	110	21.	115
7.	106	22.	110
8.	113	23.	107
9.	110	24.	111
10.	119	25.	114
11.	116	26.	109
12.	113	27.	106
13.	103	28.	107
14.	115	29.	108
15.	106	30.	96

Таблица 1

Прежде чем использовать критерии Стьюдента, Уилкоксона и другие, следует сначала проверить каждую из выборок на нормальность по критерию Колмогорова-Смирнова. Критерий согласия Колмогорова-Смирнова был разработан советскими математиками

Колмогоровым А. Н. и Смирновым Н. В. [1]. Данный критерий помогает увидеть различия между распределениями двух выборок; его также применяют для проверки на нормальность распределения совокупностей количественных данных.

Таблица 2

Одновыборочный нормальный критерий Колмогорова-Смирнова коэффициент_интеллекта_по Стенфорду_Бине

Сводка нормального одновыборочного критерия Колмогорова-Смирнова

Всего 30 Наибольшие            Абсолютная ,106 экстремальные          _ Положительные ,073 Отрицательные -,106 Статистика критерия ,106 Асимптотическая значимость (2-сторонний критерий)1 ,200ь Значимость Монте-        знач. ,518 кпитепи2й^иРиННИИ       99% доверительный      Нижняя граница ,505 '                интервал                 _ Верхняя граница ,531 а. Исправленная Лильефорса

Ь. Это нижняя граница истинной значимости.

с. Метод Лильефорса на основе 10000 выборок Монте-Карло с начальным значением 2000000.

Рисунок 1

Информация по количественным полям ко эф ф и циент_интелле кта_по Стен ф о р ду_Б ине

ко э ф ф и ци е нт_и нтел л екта_по Стенфорду_Бине

Кроме того, для принятия решения о принятии или отклонении Н0 уровень значимости всегда надо сравнивать сначала с 0,05, и если он превышает эту величину, то Н0 принимается.

Итак. У группы испытуемых тестировался интеллект по Стенфорду – Бине. Дана выборка объема n = 30. Результаты тестирования представлены в таблице 1 [6].

Следует проверить, является ли данное распределение нормальным.

Основные две гипотезы будут такими:

Н0: данное распределение нормальное.

Н1: данное распределение не нормальное.

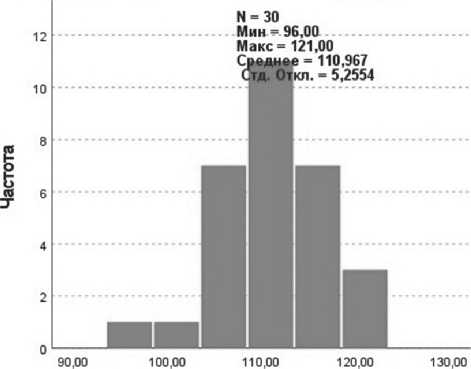
Среднее 110,967. Стандартное отклонение 5,2554.

Наибольшие экстремальные расхождения: абсолютное – 0,106, положительное – 0,73 и отрицательное – –0,106 по статистикам Колмогорова-Смирнова. Эмпирическое значение статистики критерия Z = 0,106.

Для большей наглядности накладываем нормальную кривую (Рисунок 2).

Уровень значимости (смотрим асимптотическую значимость 2-сторонний критерий) p = 0,200, что > 0,05. Нулевая гипотеза принимается.

В итоге, исходя из вышеизложенного, можно сделать вывод, что распределение является нормальным, гипотеза Н0 подтверждена.

Еще один пример применения методов математической статистики, который в рамках учебной дисциплины предлагается аспирантам: Хи2 (или критерий Пирсона) применяется для сравнения распределений объектов двух совокупностей по состоянию некоторого свойства на основе измерений по шкале наименований этого свойства в двух независимых выборках из рассматриваемых совокупностей. Применение критерия Хи-квадрат ограничивается требованием: все ожидаемые частоты должны быть больше или равны 5 [6, с. 50].

У двух групп студентов-музыкантов – с высоким (группа 1, N = 136) и средним (группа 2, N = 100) уровнем общительности – проведена диагностика развития социального интеллекта по методике Дж. Гилфорда. Данные по параметрам «гибкость» и «оригинальность». Данные приведены в таблице 4.

Таблица 3

♦ Непараметрические критерии

Итоги по проверке гипотезы

Нулевая гипотеза                   Критерий                знач.а                Решение

• 1    Распределение                 Одновыборочный критерий               ,518 Нулевая гипотеза

козффициент_интеллекта_по Колмогорова-Смирнова                        принимается.

Стенфорду_Бине является равномерным с минимумом равным 110,97 и максимумом равным 5,25543.

• а. Уровень значимости равен ,050. Метод Лильефорса на основе 10000 выборок Монте-Карло с начальным значением 2000000.

  Рисунок 2

  
  
  

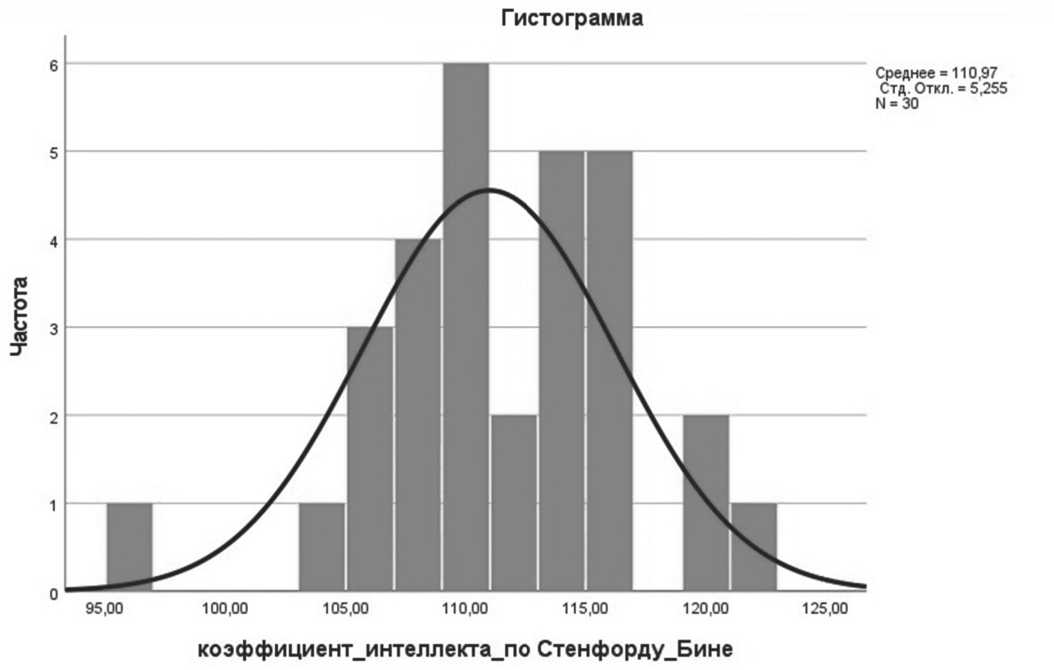
Различаются ли распределения двух категорий студентов-музыкантов по уровням развития социального интеллекта? Ответить на вопрос для каждого из двух параметров [6, с. 50–51].

Решение. Основные две гипотезы будут такими:

Н0: Нет различий между распределением двух категорий студентов-музыкантов по уровням развития социального интеллекта. Распределения двух групп по двум категориям не различаются.

Н1: Различия есть.

Сначала проверим, различаются ли распределение 2-х групп студентов-музыкантов по уровням гибкости.

Н0: Нет различий между распределением 2-х групп студентов-музыкантов по уровням гибкости.

Н1: Различия есть.

Вводим данные. Первый столбец будет означать уровень гибкости, второй – группу.

Теперь проверяем гипотезы и принимаем решение.

Итак. Из таблиц мы видим, что количе-

Таблица 4

Распределение 2-х групп студентов-музык антов по уровням гибк ости
Группы студентов-музыкантов	Предпочитаемый тип инструкции
	Низкий	Средний	Высокий
1	25	45	66
2	49	30	21
Распределение 2-х групп студентов-музыкант ов по уровням оригина льности
Группы студентов-музыкантов	Предпочитаемый тип инструкции
	Низкий	Средний	Высокий
1	30	46	60
2	22	38	40

Таблица 5

+ Таблицы сопряженности

Сводный отчет по наблюдениям Наблюдения Допустимо          Пропущенные N     Проценты     N     Проценты					Всего N     Проценты
уровень_гибкости * номер_ группы	236	100,0%	0	0,0%	236	100,0%

Таблица сопряженности уровень_гибкости * номер_ группы

номер_ группа 1		группы группа 2	Всего
уровень_гибкости низкий Количество	25	49	74
% в уровень_гибкости	33,8%	66,2%	100,0%
средний Количество	45	30	75
% в уровень_гибкости	60,0%	40,0%	100,0%
высокий Количество	66	21	87
% в уровень_гибкости	75,9%	24,1%	100,0%
Всего                         Количество	136	100	236
% вуровень_гибкости	57,6%	42,4%	100,0%

Таблица 6

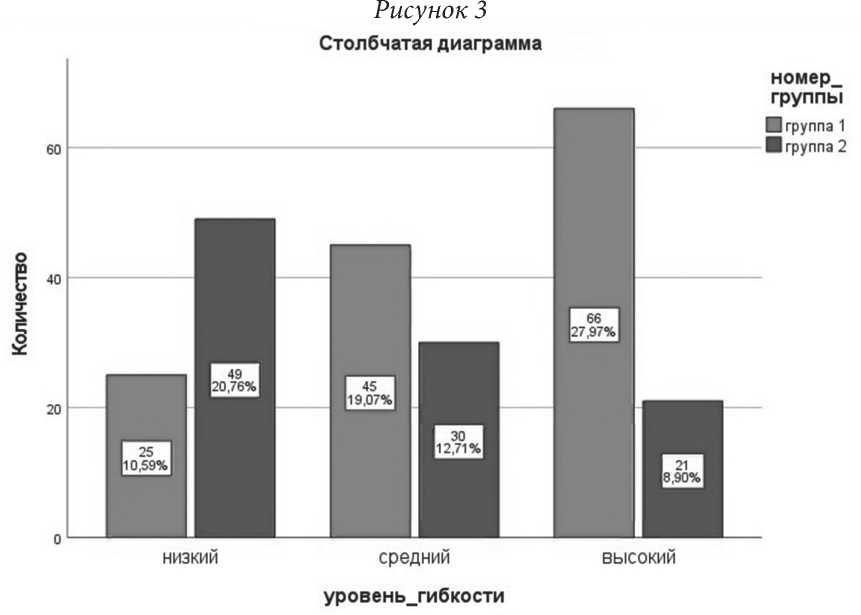
ство испытуемых (студентов-музыкантов) 236. Далее смотрим, получается, Х2эмп = 29,249, число степеней свободы df = 2 и уровень значимости p < 0,001. Очевидно, что это меньше чем 0,01 и конечно, 0,05, поэтому гипотеза H0 отвергается. Наименьшая ожидаемая частота равна 31,36. Также на столбчатой диаграмме мы видим, что различия есть по уровню гибкости.

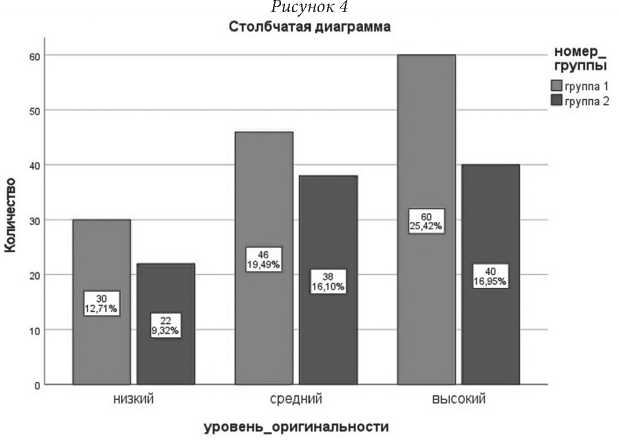
Теперь перейдем к проверке, различается ли распределение 2-х групп студентов-музыкантов по уровням оригинальности.

Н0: Нет различий между распределением 2-х групп студентов-музыкантов по уровням оригинальности.

• Н₁: Различия есть.

Вводим данные. Первый столбец будет означать уровень оригинальности, второй – группу.

Теперь проверяем гипотезы и принимаем решение.

Таким образом, из таблиц мы видим, что количество испытуемых (студентов-музыкантов) 236. Далее смотрим, получается, Х²_эмп = 0,513, число степеней свободы df = 2 и уровень значимости p = 0,774 > 0,05. По-

Таблица 7

Критерии хи-квадрат

Значение ст.св. Асимптотиче ская значимость (2сторонняя) Хи-квадрат Пирсона 29,249е 2 <,001 Отношения правдоподобия 29,878 2 <,001 Линейно-линейная связь 28,567 1 <,001 Количество допустимых наблюдений 236 а. Для числа ячеек 0 (0,0%) предполагается значение, меньше 5. Минимальное предполагаемое число равно 31,36.

этому гипотеза H0 принимается. Наименьшая ожидаемая частота равна 22,03. Также на столбчатой диаграмме мы видим, что различия есть по уровню оригинальности, но они минимальны.

В результате можно сделать вывод, что есть различия в распределении двух категорий студентов-музыкантов по уровням развития социального интеллекта: по уровню гибкости – различия есть, а по уровню оригинальности – различий нет.

Еще один пример, который мы разбираем с аспирантами. В эмпирическом исследовании у группы студентов СКД (n = 10) измерялись коммуникативные и организаторские способности (КОС).

Итоговый показатель по обеим шкалам варьируется в диапазоне от 10 до 20 баллов. Чем выше балл, тем выше уровень способностей. Данные приведены в таблице 10.

Вопрос . Есть ли связь между коммуникативными и организаторскими способностями?

Формулируем гипотезы:

• Н₀: Нет связи между коммуникативными и организаторскими способностями.

• Н₁: Связь присутствует.

В данном случае мы будем считать, что распределение является нормальным для обоих признаков и использовать Коэффициент

	Таблица 8 Сводный отчет по наблюдениям Наблюдения Допустимо           Пропущенные             Всего N     Проценты     N     Проценты     N     Проценты
уровень_оригинальност и * номер_ группы	236     100,0%         0       0,0%       236     100,0%

Таблица сопряженности уровень_оригинальности * номер_ группы

номер_ группа 1				группы группа 2	Всего
уровень_оригинальност и	низкий	Количество	30	22	52
		%в уровень_оригинальност и	57,7%	42,3%	100,0%
	средний	Количество	46	38	84
		%в уровень_оригинальност и	54,8%	45,2%	100,0%
	высокий	Количество	60	40	100
		%в уровень_оригинальност и	60,0%	40,0%	100,0%
Всего		Количество	136	100	236
		%в уровень_оригинальност и	57,6%	42,4%	100,0%

Таблица 9

Критерии хи-квадрат

Значение ст.св. Асимптотиче ская значимость (2сторонняя) Хи-квадрат Пирсона ,51 За 2 ,774 Отношения правдоподобия ,513 2 ,774 Линейно-линейная связь ,157 1 ,692 Количество допустимых наблюдений 236 а. Для числа ячеек 0 (0,0%) предполагается значение, меньше 5. Минимальное предполагаемое число равно 22,03.

Коммуникативные способности	Организаторские способности
10	12
15	18
20	19
11	10
19	17
17	20
14	13
16	13
10	12
18	15

Таблица 10. Показатели коммуникативных и организаторских способностей (КОС) в группе

Таблица 11. Данные в программе SPSS

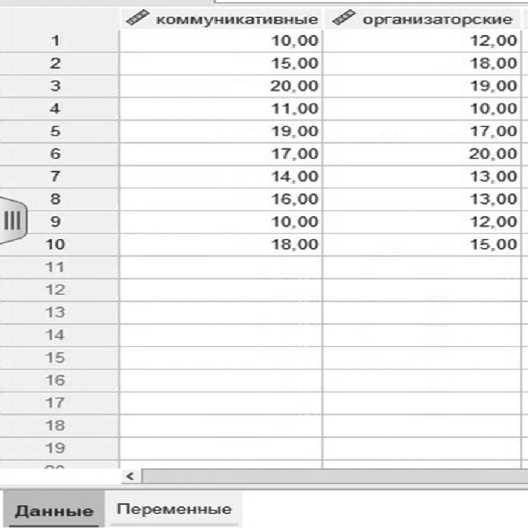
Таблица 12

* Непараметрические корреляцииКорреляции

	коммуникати вные_способ ности	организаторе кие_способн ости
Ро Спирмена коммуникативные_спос Коэффициент обности                 корреляции	1,000	,783"
знач. (двухсторонняя)		,007
N	10	10
организаторские_спосо Коэффициент бности                  корреляции	,783"	1,000
знач. (двухсторонняя)	,007
N	10	10

Корреляция значима на уровне 0,01 (двухсторонняя),