Методы параметрической оптимизации динамических систем с ограничениями типа равенства на основе задач о неподвижной точке

Распространенным подходом к решению задач параметрической оптимизации динамических систем с ограничениями является использование методов решения конечномерных задач математического программирования с неявно заданными функциями от параметров [1]. Другой подход основывается на применении теории и методов оптимального управления, в частности, необходимых условий оптимальности в форме принципа максимума [2, 3]. Предлагаемый в данной работе подход основывается на построении и реализации специальных необходимых условий оптималь- ности, интерпретируемых как задачи о неподвижной точке конструируемых операторов управления. Такие методы неподвижных точек ранее были построены и обоснованы в классах нелинейных задач параметрической оптимизации динамических систем без ограничений [4, 5]. В данной работе этот подход развивается для задач с ограничениями типа равенства.

Задача параметрической оптимизации

Рассматривается задача оптимизации управляющих параметров с терминальными ограничениями типа равенства:

x ( t ) = f ( x ( t ), u , t ), x ( t ₀) = x °, u g U c R m , t g T = [ t ₀, t 1 ], Ф i ( u ) = 9 i (x ( t 1 )) + j F_t ( x ( t ), u , t ) dt = 0, i = 1, r ,

T

Ф0(u) = ф0(x(t1)) + [F0(x(t), u, t)dt ^ min , u∈U

T в которой x(t) = (x1(t),...,xn(t)) - вектор состояния, u = (u1,...,um) - вектор управляющих параметров. В качестве доступных управлений рассматриваются векторы параметров со значениями в компактном выпуклом множестве U c Rm. Начальное состояние x0 и интервал T заданы. Функции 9i(x), Fi(x,u,t), i = 1,r, векторная функция f (x,u,t) и их производные по x и u непрерывны по совокупности аргументов (x,u, t) на соответст вующих множествах К" и R" х U х T. Функция f (x,u,t) удовлетворяет условию Липшица по x в К" х U х T с константой L > 0

II f ( x , u , t ) - f ( y , u , t )|| <  L ||x - y ||.

Рассматриваемые условия гарантируют существование и единственность решения x ( t , v ), t g T системы (1) для любого доступного управления v g U . Доступное управление u g U называется допустимым, если выполняются функциональные ограничения (2).

Определим функцию Понтрягина с вектором X = ( X ₀, X 1 ,..., X _r ) g R r ^{+ 1}

H( X , _V ,x , u , t ) = ^, f ( x , u , t )} - £ X i F i ( x , u , t ) .

i = 0

Для управления v g V обозначим ^(t, v,X), t g T - решение сопряженной системы

r

^ ⁽ t ) =— H x ^{( X ,} ^ ⁽ t x x ⁽ t x u , t ), v ⁽ t 1 ) =^- E ^X i ^ ix ^{( x (} t 1 ))

i = 0

при x ( t ) = x ( t , u ), u ( t ) = v ( t ), t g T .

Известное необходимое условие оптимальности допустимого управления u g U [2, 3] в форме дифференциального принципа максимума (ДПМ) в задаче (1)-(3) при некотором векторе X = ( X ₀, X ,..., X _r ) ^ 0, X ₀ = 0 v 1 можно представить в форме:

u = argmax ( f Hu (Л,у(t,u,Л),x(t,u),u, t)dt, w w∈U    T где Hu - производная по u функции Понтрягина.

Допустимое управление u е U , удовлетворяющее условию (4) при некотором Л = ( Л ₀, Л ,..., Л _г ), Л ₀ = 1, называется регулярным управлением. Если все допустимые управления, удовлетворяющие условию (4), являются регулярными, то задача (1)-(3) называется регулярной. В противном случае задача (1)-(3) называется вырожденной.

Условие (4) с помощью оператора проектирования P U на множество U в евклидовой норме можно также представить в эквивалентной проекционной форме:

u = P U ( u + a f H_u ( Л , у ( t , u , Л ), x ( t , u ), u , t ) dt ), a >  0.       (5)

T

Отметим, что в силу линейности сопряженной системы ее решение можно записать в следующей форме:

r

у( t, v, Л) = £ Лу1 (t, v), i=0

в которой y i ( t , v ) является решением сопряженной системы:

^{у (} t ) = ^- H x ⁽ у ⁽ t )> ^{x (} t )> ^u , t ), у ⁽ t i ) =-Ф « ^{( x (} t i )) с соответствующей функцией Понтрягина:

H i ( у ,x , u , t ) = У f ( x , u , t )) - F i ( x , u , t )

в соответствующей задаче с целевой функцией Ф i ( u ):

Ф i ( u ) = ф _i ( x ( t 1 )) + f F i ( x ( t ), u , t ) dt ^ min.

_T                        u ∈ U

Понятно, что выполняется соотношение:

r

H(Л, у , x , u , t ) = ^ \ H‘ ( у , x , u , t ).

i = 0

Следовательно, функция H соответствует функции Понтрягина в задаче с целевой функцией Лагранжа

r

L (Л, u) = ^ ЛiФi( u), i=0

и условия (4), (5) являются необходимыми условиями оптимальности (ДПМ) в задаче Лагранжа:

r

L ( Л , u ) = ^ Л ФХ u ) ^

min . u ∈ U

i = 0

Таким образом, условие (4) можно записать в эквивалентном виде: rii u = argmax ( ^ Ail Hu (у (t, u), x (t, u), u, t) dt, wi.       (6)

^weU \ i = 0 T                                    /

В приведенной классической форме условия (4) - (6) являются неконструктивными, так как остается открытым вопрос о выборе множителей Лагранжа.

Задачи о неподвижной точке с множителями Лагранжа

Задача на основе операции на максимум.

Условие (4) вместе с условием допустимости управления

Ф , (и) = 0, i = 1, r, и условием нормировки

Я ₀ = 0 v 1 представляют собой систему ( m + r + 1) уравнений с неявно заданными ( m + r + 1) неизвестными ( и , Я ). Решив эту систему, можно определить точки и е U , подозрительные на оптимальность и соответствующие им множители Лагранжа Я = ( Я ₀, Я ₁,..., Я _г ) * 0.

Предположим, что задача (1)-(3) является регулярной ( Я ₀ = 1). Тогда условие (4) с требованием допустимости управления (2) можно представить в форме следующей системы уравнений, имеющей форму задачи о неподвижной точке на множестве U х R^r :

и = argmax ( [ Н_и ( Я , ^ ( t , и , Я ), x ( t , и ), и , t ) dt , w }, weU \т / (7)

Я, = Я, + TiOi (и), Ti * 0, i = 1, r, в которой функция Понтрягина Н является регулярной (Я0 = 1) и коэф фициенты Ti * 0, i = 1, r заданы.

Для решения задачи (7) можно применить известный в вычислительной математике метод последовательных приближений и его модификации [6]. В частности метод простой итерации при к >  0 , имеющий форму:

и^{к + 1} = argmax/ [ Н_и ( Я ^к , ^ ( t , и^к , Я ^к ), x ( t , и^к ), и^к , t ) dt , w\ weU \т / (8)

Я ^{к + 1} = Я ^к + Тф i ( и^к ), T i * 0, i = 1, r .

При к = 0 задается начальное доступное приближение и ⁰ е U , Я ⁰ е R r .

Для улучшения сходимости итерационного процесса задачу о непод вижной точке (7) можно преобразовать к эквивалентной задаче:

и = и + 5 (и - arg max ( Г Н_и ( Я , ^ ( t , и , Я ), x ( t , и ), и , t ) dt , w )), w ∈ U     _T

5 * 0,

Я _i = Я _i + T i Ф i ( и ), T i * 0, i = 1, r .

Применяя метод простой итерации к эквивалентной задаче, получаем мо- дификацию итерационного процесса (8):

u^{k + 1} = u^k + 5 (u^k - arg max / f H u (X^k , ^ ( t , u^k , X ^k ), x ( t , u^k ), u^k , t ) dt , w V w ∈ U     _T

5 Ф 0,

X* ^{+ 1} = X^k + т , Ф , ( u^k ), t , Ф 0, i = 1/ r .

Основным условием сходимости метода простой итерации является выполнение свойства «сжимания» [6] для оператора правой части задачи о неподвижной точке. Поэтому, выбирая достаточно малые коэффициенты 5 Ф 0 , T , Ф 0, i = 1, r , можно регулировать сходимость рассматриваемой модификации метода простой итерации.

Задача на основе операции проектирования.

Необходимое условие оптимальности в проекционной форме (5) с условием допустимости управления (2) в регулярной задаче (1)-(3) можно также рассматривать в виде задачи о неподвижной точке на множестве U х R :

u = P U ( u + a J H u ( X , ^ ( t , u , X ), x ( t , u ), u , t ) dt ), a >  0,

T              _                 (9)

X i = X i + t , Ф , ( u ), t , Ф 0, i = 1, r .

Для решения задачи (9) можно использовать соответствующий итерационный метод последовательных приближений при k >  0 :

uk+1 = PU (uk + a J Hu (Xk ,И t, uk, Xk), x (t, uk), uk, t) dt), a> 0,                                      (10)

X,+1 = Xi + ТФ, (uk), T, Ф 0, i = v.

Оператор задачи (9) в отличие от задачи (7) является однозначным и непрерывным ввиду свойств операции проектирования P U . Это свойство существенно упрощает анализ решения задачи о неподвижной точке. При этом в качестве регулирующего параметра для анализа сходимости итерационного процесса (10) можно использовать непосредственно сам параметр проектирования a >  0.

Проиллюстрируем в рамках задачи (9) еще один подход к решению, состоящий в последовательном решении двух вспомогательных задач о неподвижной точке.

Для заданного a >  0 проведем декомпозицию поставленной задачи (9) в регулярном случае на две подзадачи.

П 1. Для заданного X е R^{r + 1}, X ₀ = 1 поиск решения задачи:

u = P U ( u + a j H_u( A,y (t , u , A ),x ( t , u ), u , t ) dt ), a >  0 . (11) T

Обозначим решение задачи (11) через uA е U и соответствующую фазовую траекторию xa (t, A) = x(t, uA), t е T. Определим векторную функцию Фa (A) = (Фa (A),..., Фa (A)) с компонентами фа (A) = ф, (xa (t1, A)) + j F, (xa (t, A), ua (t), t)dt, i = 1Г.

T

П 2. Поиск решения системы уравнений с заданными т , Ф 0, г = 1, r

A i = A i + т , Ф “ ( A ), i = 1 r .                       (12)

Понятно, что для решения A е R^{r + 1}, A ₀ = 1 системы (12) соответствующее допустимое управление u _A удовлетворяет регулярному ДПМ в проекционной форме (5).

Для реализации соотношения (11) при фиксированном A е Rr+1, A0 = 1 можно применить явный итерационный процесс с индексом к > 0 и начальным приближением u0 е U uk+1 = PU(uk + aHu(A,v(t,uk,A),x(t,uk),uk,t).

Для решения системы (12) можно использовать метод простых итераций при k >  0 и начальным приближением A ⁰ е R r ^{+ 1}, A ₀ ⁰ = 1

A+1 = Ak + т,Фa (Ak), i = 1r, регулируя сходимость процесса выбором параметров т, ф 0, i = 1, r.

Указанный подход можно рассматривать как неявный аналог известного подхода для решения систем уравнений, заключающегося в явном выражении части переменных системы уравнений через остальные переменные и переходе к эквивалентной системе меньшей размерности.

Аналогичный прием декомпозиции исходной задачи на две вспомогательные задачи можно использовать также для рассмотренных выше задач о неподвижной точке на основе операции на максимум.

Задача о неподвижной точке без множителей Лагранжа

Обосновывается новый подход к поиску управлений, удовлетворяющих необходимым условиям оптимальности в рассматриваемом классе задач параметрической параметризации с равенствами.

Приведем задачу (1)-(3) к эквивалентной форме с ограничениями типа неравенства:

x(t ) = f ( x ( t ), u , t ), x ( 1 ₀) = x ⁰, u е U c R m , t е T = [ 1 ₀, t 1 ],        (13)

Ф i ( u ) = ф , ( x ( t 1 )) + j F i ( x ( t ), u , t ) dt <  0, i = 1, r ,           (14)

T

Ф i ( u ) = - ф , ( x ( t 1 )) - j F i ( x ( t ), u , t ) dt <  0, i = r + 1,2 r , (15)

T

Ф ₀( и ) = ф ₀( x ( / 1 )) + [ F ₀( x ( t ), и , t ) dt ^ min . u ∈ U

T

Понятно, что в задаче (13)-(16) все ограничения типа неравенства являются активными:

Ф ' ( и ) = 0, г = 1,2 r .

Определим множество I индексов активных ограничений вместе с индексом целевого функционала:

I = { 0 } и { ' = 1,...,2 r : Ф ' ( и ) = 0} .

Рассмотрим множество

Л = { Л = ( \ ,' е I ): \> 0, £ Л = 1} .

∈ I

Известное необходимое условие оптимальности допустимого управления и е U [2, 3] (ДПМ) для задачи (13)-(16) при некотором ЛеЛ можно представить в виде неравенства:

।, w е U. (17)

Из неравенства (17) следует, что min λ∈Λ

।, w е U .      (18)

Неравенство (18), согласно известному результату (Лемма 3.1 на стр. 108 в [7]), эквивалентно неравенству min( [HU (у' (t, и), x(t, и), и, t)dt, w - и ) i∈I

T w е U. (19)

Таким образом, получаем следствие необходимого условия оптимальности (17) в форме соотношения (19) без множителей Лагранжа.

Условие (19) можно представить в форме следующей задачи о неподвижной точке на множестве U :

и = argmaxmin( \ H ^l _u (у¹ ( t , и ), x ( t , и ), и , t ) dt , w - и )V (20) w ∈ U ∈ I

T

Для численного решения задачи (20) можно применить итерационный процесс простой итерации при к >  0 и начальным приближением и ⁰ е U :

и^{к + 1} = argmaxmin/ [ H U ( у ' ( t , и^к ), x ( t , и^к ), и^к , t ) dt , w - и ^к ) w ∈ U ∈ I

T и его модификации для улучшения сходимости.

Отметим, что решения задачи (20) являются лишь доступными управлениями, т. е. ограничения типа равенства (2) не обязательно выполняются для решений задачи (20). Обозначим U * множество решений задачи (20).

В итоге решение задачи о неподвижной точке (20) позволяет сузить множество U доступных управлений до множества U * «приближеннооптимальных» управлений, для которых выполняются необходимые условия оптимальности, но которые могут быть недопустимыми управлениями.

Дальнейший анализ полученных решений задачи о неподвижной точке (20) сводится к выбору среди них допустимых управлений, т. е. решению системы уравнений:

Ф i ( и ) = 0, i = 1, r, и е U* . (21)

Предлагаемый подход позволяет сделать важные выводы о существовании и структуре множества оптимальных управлений уже на первом этапе поиска приближенно-оптимальных управлений. Полученные приближенно-оптимальные управления могут быть использованы в качестве обоснованных начальных приближений для итерационных процессов решения задач о неподвижной точке с множителями Лагранжа, которые были рассмотрены в предыдущем разделе.

В целом разработанный подход можно рассматривать как последовательную декомпозицию задачи поиска управлений, удовлетворяющих необходимому условию оптимальности (19), на задачу поиска неподвижной точки на множестве доступных управлений (20) и задачу решения системы уравнений на полученном множестве неподвижных точек предыдущего этапа (21).

Примеры

Проиллюстрируем предлагаемые методы неподвижных точек на простом примере:

x(t ) = и , x (0) = 0, и е U = [ - 1,1], t е T = [0,1],

Ф , ( и ) = x (1) - a = 0,

Ф ₀( и ) = j ( x ²( t ) - и ²) dt ^ min.

В данной задаче тривиально определяется единственное допустимое управление и = а при | а | <  1, которое в силу единственности является оптимальным. При | а | >  1 в задаче нет допустимых управлений, т. е. задача не имеет решения.

Проведем анализ этой простой задачи предлагаемыми в работе методами.

Метод с множителями Лагранжа .

Имеем H = у и - Л ₀ ( x ² - и ²) и сопряженную систему:

у ( t ) = 2 Я ₀ x ( t ), у (1) = - Д .

Условие оптимальности (4) принимает вид:

u = arg max ( ( ^ ( t , u ) + 2 1 0 u ) dt , w ).

w51 \T

В данном примере легко выписываются общие решения фазовой и сопряженной систем: x ( t , u ) = ut , y (t , u ) = 1 ₀ ut ² - 1 ₀u — 1 1 , t e T , u e U , с помощью которых можно провести следующий анализ регулярности и вырожденности рассматриваемой задачи.

Предположим, что 1 ₀ = 0 (вырожденная задача). В этом случае 1 1 Ф 0,

^ ( t , u ) = —1 1 , и из условия оптимальности следует управление

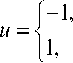
1 1 >  0,

1 < 0.

Отсюда получаем для t e T

I — t , x ( t ) = 1

1 >  0,

1 1 <  0.

I t ,

Следовательно, если a ^± 1, то получаем противоречие условию допустимости управления, т. е. x (1) ^ а .

Таким образом, в случае | а | ^ 1 задача является регулярной.

В случае | а | = 1 существуют допустимые управления и множители Лагранжа 1 1 ^ 0 с 1 ₀ = 0, удовлетворяющие необходимому условию. В данном случае задача является вырожденной.

Далее проведем анализ существования неподвижных точек задачи вида (7) для регулярного случая | а | ^ 1.

Положим 10 = 1. Отсюда следует общее решение сопряженной системы ^(t,u) = ut2 — u — 1, t e T и задача о неподвижной точке с заданным т1 ^ 0:

/ 4 , \ . 4 а u = arg max ( — u — 1 1 , w ) = sign I — u — 1 1 I , I w ^{5 1} \3                        1 3          )

Решениями первого уравнения являются граничные неподвижные точ- 44

ки: u = 1 при 1 5 у; u = — 1 при 1 1 >—— ; а также внутренние неподвиж-

3 .   „              , 4

ные точки u = — 1 e U при Ц< — , удовлетворяющие условию:

—u — 1 = 0 (так называемые «особые» точки [4]).

Из этих неподвижных точек условию допустимости управления (вто.                  :           .    4

рое уравнение) удовлетворяют лишь особые точки и = —^ при ^ = —a .

При этом условие доступности управления

। 4i < 3

выполняется для | a | < 1

и не выполняется при | a | >  1.

В итоге проведенного анализа получаем, что задача о неподвижной точке в регулярном случае при |a| < 1 имеет единственное решение и = a, которому соответствует множитель Лагранжа ^ = ^a . В силу указанной единственности, а также существования оптимального решения исходной задачи, управление и = a является оптимальным. При |а| > 1 допустимых управлений нет, и задача оптимизации не имеет решения.

Таким образом, метод неподвижных точек с множителями Лагранжа в рассматриваемой регулярной задаче позволяет определить ее решение.

Метод без множителей Лагранжа.

Проведем анализ существования неподвижных точек задачи вида (20).

Задачу оптимизации приведем к требуемому эквивалентному виду с ограничениями типа неравенства:

x ( t ) = и , x (0) = 0, и е U = [ - 1,1], t е T = [0,1],

Ф 1 ( и ) = x (1) - a <  0,

Ф ₂( и ) = - x (1) + a <  0,

Ф ₀( и ) = j ( x ²( t ) - и ²) dt ^ min.

В полученной задаче:

• 1)    функции Понтрягина H ¹ = у и соответствует сопряженная система: у ( t ) = 0, у (1) = - 1, которая имеет общее решение у 1 ( t , и ) = - 1, t е T , и е U ;

• 2)    функции Понтрягина H ² = у и соответствует сопряженная система: у ( t ) = 0, у (1) = 1, которая имеет общее решение у ²( t , и ) = 1, t е T , и е U ;

• 3)    функции Понтрягина H ⁰ = у и - ( x ² - и ²) соответствует сопряженная система: у ( t ) = 2 x , у (1) = 0, которая имеет общее решение

у ⁰( t , и ) = ut ² - и , t е T , и е U .

С учетом полученных выражений задача о неподвижной точке (20) в рассматриваемом примере принимает вид:

f                    ⁴

и = arg max min ] - ( w - и ),( w - и ), —и ( w - и )

Рассматривая несложную графическую интерпретацию этой задачи для различных случаев доступных значений | и | <  1, можно легко получить следующий вывод: любое доступное управление | и | <  1 удовлетворяет этой задаче о неподвижной точке.

Дальнейший анализ условия допустимости х (1) = а для доступных управлений | и | <  1 с помощью общего решения фазовой системы х ( t, и ) = ut, t g T, и g U приводит к единственному допустимому управлению и = а при | а | <  1. В силу единственности этого допустимого управления и существования оптимального решения исходной задачи данное управление является оптимальным. При | а | >  1 допустимых управлений не существует, поэтому задача оптимизации не имеет решения.

Таким образом, в данном простом примере метод неподвижной точки без множителей Лагранжа позволяет получить полное решение оптимизационной задачи.

Рассмотренные примеры практического применения методов наглядно демонстрируют их основные конструкции и в определенной степени иллюстрируют работоспособность предлагаемых методов.

Заключение

Предложены новые конструктивные подходы к поиску экстремальных управлений в рассматриваемом классе задач параметрической оптимизации с ограничениями типа равенства с помощью решения специальных задач о неподвижной точке определяемых операторов управления . Разработанные подходы выгодно отличаются от известных градиентных методов отсутствием трудоемкой операции варьирования допустимого управления на текущей итерации для обеспечения последовательного улучшения и допустимости итерационных приближений управления. Рассматриваемые итерационные процессы последовательных приближений для решения рассматриваемых задач о неподвижной точке сводят решение оптимизационной задачи к последовательному решению чередующихся фазовых и сопряженных задач Коши без операции варьирования управления на каждой итерации. При этом построены модификации процессов без использования множителей Лагранжа и обоснован выбор доступных начальных приближений для процессов. Указанные особенности являются важными факторами повышения вычислительной эффективности решения рассматриваемого класса нелинейных задач параметрической оптимизации с ограничениями типа равенства.