Методы построения энергетически оптимальных алгоритмов движения шагающих машин

Одним из сдерживающих факторов развития и широкого применения шагающих машин является низкая энергетическая эффективность их приводов. Необходимая для обеспечения мощность двигателя в приводе курсового движения шагающих машин пропорциональна кубу скорости 2, что значительно ограничивает увеличение скорости движения шагающих машин.

Известны различные варианты уменьшения энергозатрат, связанных с периодическим разгоном-торможением неуравновешенных движителей машины: увеличение отношения продолжительности фазы переноса к продолжительности опорной фазы (увеличение коэффициента режима механизма шагания) 3, введение в схему механизма шагания рекуператора механической энергии 4 . Однако эти меры приводят к усложнению конструкции машины, увеличению ее массы и снижению КПД приводов, эффективность работы рекуператора зависит от скорости движения машины, что затрудняет его использование при переменных режимах движения.

Для шагающих машин с цикловыми движителями правомерна модельная задача определения такого закона изменения относительной горизонтальной скорости опорной точки механизма шагания, при котором мощность приводного двигателя во время движения будет постоянна и минимальна.

Примером шагающей машины, для которой может быть поставлена такая задача, является шагающая машина «Восьминог»5 массой 4,5 т (рис. 1). Для существующего привода данной машины при средней скорос- ти движения Vcp = 0,068 м/с максимальное значение реактивной мощности привода, требуемое на поддержание курсового движения машины без учета энергозатрат на работу по преодолению сил тяжести и сил сопротивления, – менее 5 Вт, а при скорости 1,5 м/с требуемая мощность превышает 53 кВт.

В рамках принятой постановки модельной задачи оценки энергозатрат машина представляется системой трех твердых тел (рис. 2): корпуса и двух стоп, соединенных друг с другом безынерционными обратимыми механизмами и приводимых в движение одним двигателем, что соответствует кинематической схеме шагающей машины «Восьминог» с одностепенными движителями, и не может быть распространена на общий случай движителей с большим числом степеней подвижности и (или) с индивидуальными приводами. Рекуперация энергии происходит следующим образом. В той фазе цикла шага, когда требуется ускоренное движение переносимой стопы, вторая стопа, находящаяся в опоре, и корпус машины движутся замедленно. За счет инерции корпуса, момент на ведущем валу второго механизма шагания становится отрицательным, и при постоянстве момента, развиваемого двигателем, момент на ведущем валу первого механизма возрастает. Таким образом, перераспределение кинетической энергии осуществляется от корпуса к ускоренно движущемуся механизму шагания и, аналогично, в обратном направлении при замедлении механизма шагания. Следовательно, при соответствующем выборе параметров механизма шагания и управления можно добиться того, чтобы мощ- ность, развиваемая двигателем, оставалась постоянной и была минимальной.

При этом движение стоп относительно корпуса должно задаваться таким образом, чтобы в каждый момент времени одна из стоп находилась в опоре, а вторая в переносе – этим обеспечивается статическая устойчивость машины.

Уравнения движения рассматриваемой механической системы, имеющей один общий привод для механизмов шагания, находящихся в опорной фазе и фазе переноса, включают в себя дифференциальные уравнения движения тел, уравнения связей, устанавливающие зависимость между перемещением ведущего звена и перемещением корпуса машины и переносимого механизма шагания и уравнение двигателя при постоянной скорости выходного звена при действии постоянной силы сопротивления движению Q :

Mx1 - 21 — Q, mx2 - 22,

< x i ^- П i ( ф )^- 0, x 2 — П 2 ( Ф ) - 0,

L - 2 , д П 1

¹ d ф

-

2 2 П - 0; d Ф

где M , m

– масса корпуса машины и эквивалентная масса звеньев меха- низмов шагания, находящихся в фазе переноса, приведенная к опорной точке;

x1, x2      – абсолютные горизонтальные ко ординаты корпуса машины массы M и опорной точки переносимого механизма шагания массы m;

X , , X ₂     - неопределенные множители

Лагранжа;

Рис. 1. Шагающая машина «Восьминог»

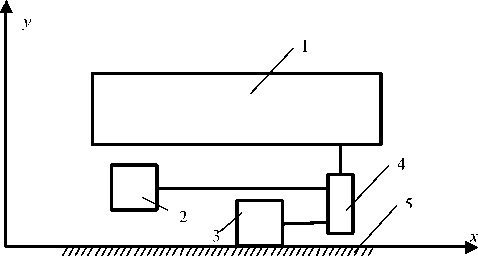
Рис. 2. Модельная схема поступательного движения шагающей машины:

1 – корпус; 2 – эквивалентный механизм шагания в фазе переноса; 3 – эквивалентный механизм шагания в фазе опоры;

4 – привод курсового движения; 5 – грунт

φ

П ₁( ϕ ), П ₂( ϕ )–

L

обобщенная координата приводного двигателя (например, угол поворота), при этом ф = го = const ;

передаточные функции, определяющие голономные стационарные связи между двигателем и рассматриваемыми телами;

генерируемая двигателем обобщенная сила (в рассматриваемом случае момент).

Полагая, что необратимые потери мощности W пропорциональны квадрату генерируемой обобщенной силы L , что, например, характерно для двигателей постоянного тока

W = αL ²,               (2)

Тогда уравнения Эйлера имеют вид:

• ²    ( ^{T +} Q ^X i ) m 2 ^X 2 = М 2,

• 2    ( T + QXi ) m i X i - 2 Q ( T + Qx ) = щ.

При выполнении граничных условий

• ^X2 ⁽⁰⁾ = ^X2 ( У 2 ) = 0, - x l C ⁰ ) = x i ( T 2 ) = -x iO , (9) где X i 0 — скорость шагающей машины в момент смены опорных точек механизмов шагания, входящих в движитель (в момент переступания).

22.                 _

При наложении граничных условий (9) следует µ ₂ = 0 и µ ₁ = –4 Q ² S / τ .

Поэтому, где a - постоянный коэффициент пропорциональности.

T + Qx i = 0,

С учетом того, что

и остается одно содержательное уравнение

дП .    . д П^ .   .

Ф = ^xi,^2 Ф = ^x 2 , д ф        д ф

T + Qx i = 2 QT = QV cp ,

после преобразований уравнений (1) имеет место уравнение

L(p = T + Qx i .

Для того чтобы минимизировать потери энергии, необходимо обеспечить минимум функционала

которое при Q = 0 сводится к известному ранее результату⁶ T = 0, , где V cp - средняя скорость движения шагающей машины.

Если задать требование минимальности и постоянства модуля ускорения корпуса машины, то получается равноускоренный закон его движения

τ 2            τ 2

A = a J L ² dt = 0 2 J ( T + QX_i ) ² dt , (5)

0        Ф 0

x i = i

τ

X i0 — at , 0 <  t <  —,

t [ xiл — a— + a t i0 4 I

T 1 T

τ

—

- ,-< t < -.

4 ) 4      2

при учете дополнительных условий

τ 2         τ 2

J X i dt = S , J X 2 dt = 2 S ,        (6)

где S – длина шага механизма шагания;

τ – период движения.

С учетом (6) функционал (5) можно рассматривать как

Дальнейший анализ удобно производить в безразмерных параметрах и достаточно рассмотреть движение при 0 <  t <  у» . Зависи- ττ ⁴

мость X 2 = X 2 ( t ) при 4 <  t <  2 будет симметрична относительно оси t = ^T 4.

Методами теории подобия вводятся следующие безразмерные критерии:

T 2 Г .         ₂                1

J = J ( T + Qx i ) + M i x + М 2 ^x2 ^dt , (7)

0 L                           J

где µ ₁, µ ₂ – неопределенные множители Лагранжа.

Q q = Mda — безразмерная сила сопротивления;

9 = -ta x10

– безразмерное время;

W =---ю - угол поворота ведущего звена ме-a ханизма шагания (для шагающей машины «Восьминог» угол поворота кривошипа), при котором, двигаясь равнозамедленно с ускорением а, шагающая машина останавливается; ю = ф угловая скорость ведущего кривошипа механизма шагания.

_ Х2

v2 = ~  - безразмерная скорость опоры ме- x10

ханизма шагания в фазе переноса.

Тогда из (11), с учетом (12), следует

4 ψ

V 2 = в ( q - ^{1 ) 9 2} + ² [ 1 - 4 П >. (13)

Так как квадрат безразмерной скорости опоры механизма шагания ν ₂ ² должен быть больше нуля, то имеют место ограничения, накладываемые на безразмерные параметры q и ψ .

Учитывая, что

ππ

0 < 9 < —; w >—,

2 ψ       4 ^,

то имеется одно содержательное условие

1 - qn >  0, 4 ψ

или в физических переменных где R

Q <  —MRm ² ,          (16)

π условный приведенный радиус механизма шагания (радиус колеса эквивалентного по кинематическим характеристикам данному механизму шагания), определяемый из соотношения

X 10 = R to .                (17)

Окончательно определяется требуемый закон переноса механизма шагания в относительном движении x 2 r = x 2 - x 1 = П₂( ф ) - П 1 ( ф ) относительно корпуса машины как разность абсолютных движений опорной точки переносимого механизма шагания и центра масс корпуса машины.

При учете силы сопротивления, зависящей от скорости, дифференциальные уравнения движения отличаются от (1) и имеют вид

Mx1 = 21 - Q(Ху), mx2 = 22, x1 = П1 (Ф), x2 = П2 (Ф),

L - 2 , д П - 2 2 ®2 = 0.

1 d ф      dф

Как и в предыдущих случаях, имея в виду, что ф = to = const, требуется минимизировать функционал (7) при выполнении изопериметричеcких условий (6).

Тогда уравнения Эйлера имеют вид:

2\t + dQdtr x ' + Q ( x ¹) ^{8 1} ] Mx 1 - 2 Г t + Q (1 x 1 ) x j[ Q (1 x 1 )' ' Qx 1 ) 1 x 1 ]= ^ 1 ,

Гт T ^d Q ( x >-^n r-v]

21 T + d ' x 1 + ^{Q (} x 1 ) x 1 mx 2 = ^ 2 .

Из граничных условий (9) и анализа второго уравнения (19) следует ц ₂ = 0, и тогда первое уравнение (19) имеет вид:

2 Г T + Q ( x ) x ] Q ( x ) +^{d Q} ( x ¹. x о x 1

= ^ 1 -(20)

Дифференциальное уравнение (20) можно проинтегрировать, если задаться видом функции Q ( \ '|) . Например, для Q (, \ '|) = kx ^ , где k – коэффициент пропорциональности. В этом случае (20) сводится к виду:

- 2 Г T + kx ² ^| [ 2 kx 1 ] = ^ 1.

При интегрировании данного дифференциального уравнения с учетом следствия из (19):

T + ^{dQ (} x^{1 , x 1)} x + Q ( ^cx , x 1 ) x = d Г T¹ + Q ( ^^1 , x 1 ) ^^1 ] = 0, (22)

_ dt                   J dr- получается

T + Q ( x 1 ) x 1 = const = T 0 + Q (- x 10 ) - x 10 =- Mx 10 a + kx 20 . (23)

Уравнение (21), таким образом, решить невозможно, так как произведение в левой части должно быть константой ввиду того, что в данной изопериметрической задаче множи- тель Лагранжа ц1 - константа, а "1 - при выбранном законе движения корпуса константой не является. Однако минимум энергозатрат можно определить, задавшись требованием равнопеременного движения корпуса машины, аналогичным следствию (12) системы уравнений (8). В таком случае в исследуемом функционале остается один неопределенный множитель Лагранжа, а в системе (19) – одно второе уравнение, которое дает первый интеграл:

- т + ^dQ( " 1 ) "^ 1 + Q ("^ 1 ) " ]= d - т + Q (о " 1 ]= 0 ^ т + Q ( " ) " 1 = const . (24)

Причем коэффициент из правой части уравнения (24) может быть определен, как и ранее, из наложения первого из изопериметрических условий (6), как средняя мощность сил сопротивления за период:

τ 2                  τ 2 τ 2 τ 2              τ

J - T + Q ( " ) с ] dt = J Cdt / J Tdt + J Q ( " ) " 1 dt = C |. (25) 0        0   00       2

Учитывая, что в силу (9) изменение кинетической энергии за период равно нулю, и задавшись линейной зависимостью силы сопротивления от скорости, получаем, переходя к безразмерным параметрам:

^{T 2}            r ^ ^{( 2} ^ )       2     ^{n ( 2} ^ ) f   _n ^ ²

J k5 c 2 dt = k"²    J    ( 1 - 9 j d 9 +    J    1 1 + 9 I dt

0                0                0   V    2 v )

T

= ^C 2 ,(26)

откуда после соответствующих преобразований получаем:

_C = ^{4 k} " 1²0 , τ

1 + 2 n

r 1     1 )

—

I w2  V J_

.

Окончательно, для данного случая, также как и для случая постоянной силы сопротивления движению, при подстановке (27) в следствие из уравнения (24) может быть определен требуемый закон переноса опорной точки механизма шагания в относительном движении при различных значениях коэффициента пропорциональности линейной зависимости силы сопротивления от скорости.

Полученные результаты позволяют определять кинематическую характеристику циклового механизма шагания, который будет обеспечивать минимум энергозатрат при движении.