Метрики сложной детерминированной системы

Несмотря на широкое употребление термина «сложные системы» до настоящего времени не разработано чётких критериев оценки сложности и сопоставимости сложных детерминированных систем. Это обусловлено тем, что понятие сложности является полисемическим и употребляется как атрибут и как субстанциональное понятие. Примерами сложности могут быть: сложность вычислений, топологическая сложность графа, технологическая сложность интерфейса, сложность управления подвижным объектом, сложность определения координат быстролетящих объектов, сложность определения точки падения космического объекта, сложность аппроксимации рельефа, сложность алгоритма, сложность генетического кода, сложность случайных взаимодействий, сложность нелинейных процессов и др.

При исследовании проблемы сложности часто сужают это понятие, либо используют его как атрибут другой проблемы. Так в работе [1], посвящённой междисциплинарному переносу знаний, сложность является препятствием типа информационного барьера. По существу рассматривается один вид сложности - сложность коммуникации между разными научными направлениями, и делается вывод - развитие трансдисциплинарности уменьшает сложность.

В работе [2], посвященной глобализации, рассматривается один вид сложности, обусловленный глобальными процессами, где по существу идеология управления аналогична управлению рисками, которые на практике сводятся к их минимизации. В работе [3] сложность связывают со сложностью хаоса или непредсказуемостью внешней среды. Технологическая сложность применения программного обеспечения (ПО) рассматривается в работе [4], где управление сложностью сводится к рекомендациям устранения трудностей при внедрении ПО. Здесь понятие «сложность» используют как синоним понятия «трудность».

Большое количество работ о сложности написано Ржевским Г.А. [5-7]. В работе [7] следует считать важным анализ различий, которые делают авторы между понятием «сложность» (complex) и «усложнение» (complicated) [7, таб.1]. Этим они разграничивают сложные системы от усложненных, но не сложных систем. Авторы вводят понятия стохастической и детерминированной систем [7, таб.2], не относя их к сложным системам. Это противоречит работам в области синергетики [3], в которых стохастические системы рассматривают как сложные системы.

«Сложность является свойством открытой системы, состоящей из большого числа разнообразных, частично автономных, богато взаимосвязанных компонентов, часто называемых агентами, не имеет централизованного контроля и чье поведение возникает из сложного взаимодействия агентов и поэтому неопределенно, не будучи случайным» [7, с.5]. В соответствии с этим определением все закрытые (а это технические системы и программные системы) из сложных систем исключаются. Авторы дают семь признаков сложной системы, которые «отличает сложные системы от детерминированных и случайных: связность, автономию, эмерджентность, неравновесность, нелинейность, самоорганизацию и коэволюцию». Эти признаки исключают детерминированные системы из числа сложных систем.

Трактовка сложных систем по Ржевскому [7] отлична от определений сложных систем, даваемых в работах по системному анализу Берталанфи [8], Месаровичем [9], Уемова [10], в которых сложная система определяется как закрытая система, имеющая совокупность устойчивых связей.

Детерминированные системы, за исключением работы [4], в публикациях [1-7] не рассматривают и к сложным системам не относят. Поэтому целью данной работы является исследование сложности детерминированных систем. Существует достаточно большое количество различных детерминированных систем, которые с разной степенью можно отнести к сложным системам:

• ■    прикладная система [11] (алгоритмическая система);

• ■    система обработки данных;

• ■    банк данных, сложная техническая система;

• ■    сложная социотехническая система [12];

• ■    сложная организационно-техническая система [13];

• ■    сложная социальная система [14] и другие.

В тоже время системный анализ и теория систем по существу уходят от анализа сложных систем и рассматривают довольно простую модель сложной системы, содержащую гомогенные (однородные) элементы и типовые связи [8-10]. В системном анализе сложной системой называют множество элементов, находящихся в отношениях и связях друг с другом, которые образуют определённую целостность и единство, обладающее новым качеством, не присущим отдельным элементам [15]. Гетерогенность элементов в этом определении отсутствует. Определения сложных систем, даваемые в [8-10, 15], одинаково описывают систему, содержащую 10 и 10 000 000 элементов. Однако очевидно, что сложности таких систем существенно различаются. Кроме того, система, которая содержит всего 100 элементов и система, содержащая 100 элементов, но повторяющихся по 100 раз, то есть всего 10 000 элементов также имеют разную сложность, что не отражают определения сложных систем [8-10, 15]. Применяемые по существу «простые модели сложной системы» [8-10] не в состоянии учесть различия и разные аспекты сложности перечисленных выше реальных систем. В аспекте современной проблемы «больших данных» [16] сложность систем можно связывать с большим информационным объёмом, большим числом связей, с когнитивными факторами: необозримости, невоспринимаемости, неинтерпретируемости, непереносимости характеристик с одной системы на другую. Сложность можно связывать с понятием «большие графы» [17] и с соответствующими методиками их обработки. Возникает необходимость связать понятие сложности с размером системы и ввести некий сравнительный критерий оценки системы в зависимости от количества элементов этой системы.

По мнению авторов, в отличие от [1-7], некоторые сложные программы можно рассматривать как пример сложных систем. Поэтому наработки в области анализа ПО целесообразно использовать в качестве метрик сложной системы, которые позволят сравнивать разные детерминированные сложные системы между собой на основе объективных критериев. Цель данной статьи - обоснование модели метрики сложной детерминированной системы как критерия сложности.

1 Материалы и методы. Анализ метрик Холстеда

В основе данной работы лежит подход к оценке качества ПО и элементы математической теории коммуникации К.Э. Шеннона [18], а основой в оценке качества ПО являются метрики Холстеда [19, 20], позволяющие получить численное значение сравнительной характеристики ПО. Следует отметить, что большая часть оценок ПО, которую предлагает Холстед, является эмпирической, условной и даже спорной. Интерес представляют сами идеи получения той или иной оценки.

Условность состоит в том, что Холстед рассматривает только ПО и только последовательные программы и не рассматривает сложные системы. Базовые характеристики, которые использует Холстед, следующие [19]:

• П 1 - число различных операторов или базис операторов;

• П ₂ - количество различных операндов или базис операндов;

• N 1 - общее число операторов в программе;

• N 2 - общее количество операндов.

Величины п 1 и п 2 можно рассматривать как алфавит или основание кода. В дальнейших работах последователей Холстеда греческие буквы п 1 и п 2 были заменены на латинские символы п 1 и n ₂. Это упрощает нотацию и не влияет на ход рассуждений. Наибольший интерес представляет метрика, которую Холстед называет расчётной длиной программы.

• (1)                                IN = n 1 log₂ n 1 + n₂ log₂ n₂ .

Обозначение IN введено авторами настоящей статьи. У Холстеда эта величина выражена через N c надчёрком. Расчётной длине программы Холстед противопоставляет фактическую или физическую длину программы

• (2)                              N=N 1 +N .

Холстед также вводит величину n = n 1 + n ₂, которая характеризует общее число операторов и операндов. Различие между выражениями (1) и (2) в том, что выражение (1) даёт оценку в битах, а выражение (2) даёт оценку в количестве информационных единиц [21], которые в данном случае являются операндами и операторами.

Проанализируем выражение (1) с позиций информационной теории. Здесь дискретная случайная величина X называется m-ичным символом, если множество её возможных значе- ний x1, x2, ..., xm определено. Это множество называют алфавитом, а число m - основанием кода или объёмом алфавита. В случае метрики (1) имеем два основания кода п1 и n2. Количество возможных вариантов разных сообщений:

• (3)    Ns=mⁿ ,

где Ns — возможное количество различных сообщений; m — количество букв в алфавите; n— количество букв в сообщении. В выражении (3) n является аналогом N в выражении (2). Количеством информации по Хартли называют характеристику

• (4)    I=log 2 Ns=n log₂m ,

где I — количество информации (бит). Часто вместо Ns используют N . Но чтобы избежать путаницы с обозначениями Холстеда вводим Ns . При равновероятности символов p=1/m; m=1/p , формула Хартли (4) переходит в собственную информацию [22, 23] символа, то есть информационную ёмкость [23]. Применительно к состояниям или к элементам информационного языка выражение (4) оценивает количество информации на одно состояние или количество информации на один символ сообщения.

Таким образом, в метрике Холстеда (1) стоит сумма двух энтропий, то есть количество информации, которую содержат два алфавита, образующие программу. Это даёт основание трактовать выражение (1) как информационную длину программы, что и обусловило введение авторами статьи символа I в дополнение к символу N.

Определение 1 : информационная длина программы - это количество информации в битах, которое содержат алфавиты, образующие эту программу.

Данная трактовка является информационной трактовкой метрики Холстеда (1). Топологическая модель метрики Холстеда приведена на рисунке i.

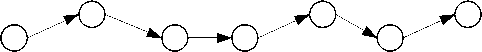
Операнд

Оператор

Рисунок 1 - Топологическая модель метрики Холстеда

Как следует из рисунка 1, топологическая модель метрики Холстеда описывает линейную систему с наличием только двух групп элементов. Для линейных последовательных программ такая схема приемлема. При этом такая система является упрощением, поскольку не включает циклы и связи между однотипными элементами. Она не приемлема для параллельных вычислений и сетей Петри. На рисунке 2 показана схема реальной программы, которая не описывается метрикой Холстеда.

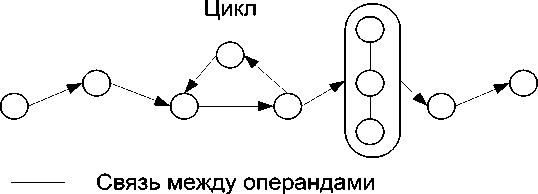
Рисунок 2 - Схема программы с циклом и дополнительными связями

Схема на рисунке 2 включает два дополнительных элемента: цикл и связи между опе- рандами. В схеме на рисунке 1 оператор выполняет функции связи единственного вида. Можно констатировать, что метрика Холстеда (1) является упрощённым описанием только линейной системы без циклов и дополнительных связей. Следовательно, она имеет ограниченную область применения.

Ещё одна характеристика, которую вводит Холстед, это условный информационный объём, определяемый по формуле

• (5)    V=N log 2 n.

С геометрической точки зрения выражение (5) описывает не объём, а площадь. В соответствии с формулой Хартли выражение (5) описывает логическое количество информации, которое содержит реальная программа, то есть произведение информационных единиц программы (операнды и операторы) и бит словаря без учёта информационной ёмкости каждой единицы. Величина N не учитывает объёмы информационных единиц. Величина log 2 n не учитывает отсутствие элементов словаря в программе, подразумевая, что все элементы словаря использованы в программе. Это ограничивает применимость методик Холстеда. Давая общую характеристику введения метрики Холстеда, можно назвать его подход формально лингвистическим или просто лингвистическим.

Вывод. Большинство метрик Холстеда не адекватно метрикам сложных систем и не может быть без переработки перенесено в теорию сложных систем. Однако отдельные метрики и идеи могут использоваться для построения метрик сложных систем и для сравнения сложных систем. Метрика Холстеда учитывает только два типа информационных единиц.

2    Моделирование и метрики 2.1    Моделирование сложных систем

В зависимости от исходных концепций при описании сложных систем получают разные модели систем и разные трактовки. По мнению авторов, работа [24] наиболее адекватно описывает систематику современных сложных систем, т.к. она рассматривает стохастические системы и детерминированные системы, анализирует саморазвивающиеся и закрытые системы, включая в себя теорию систем [8-10]. В соответствии с [24, с.5] в теорию сложных систем входят эмерджентизм [25] и самоорганизация [26]. Она связана с теорией игр, коллективным поведением, теорией распределённых систем, эволюцией и адаптацией, нелинейной динамикой [1-7].

Сложными системами называют сетевые системы, которые имеют большое количество компонент, взаимодействующих друг с другом, для которых типичными являются нелинейные функции [24, с.3]. Авторы данной статьи разделяют точку зрения Hiroki Sayama [24], однако считают более точным заменить термин «сетевые системы» на термин «распределённые системы». Анализ работы [24] показывает, что понятием сетевые системы автор фактически обозначает сетевую структуру, а не сетевые системы. Целесообразность использования понятия «распределённые системы» в альтернативу «сетевым системам» подтверждается современным развитием технологий Интернет-вещей [27] и технологиями кибер-физических систем [28]. Оба эти вида систем относятся к сложным и распределённым системам.

Модель сложной системы должна быть воспринимаема, валидна и надёжна. Воспринимаемость [29] – когнитивный фактор и его иногда избегают, заменяя термином простота. В развитие понятия Ржевского «усложнение» [7] можно ввести понятие «упрощение» и разграничивать понятие простая система от понятия «упрощённая сложная система».

Валидностью модели сложной системы называют качество информационного соответствия, которое показывает то, насколько точно предсказание поведения сложной системы согласуется с наблюдаемой реальностью [24]. Это имеет первостепенное значение с практической точки зрения. Если предсказание поведения сложной системы не соответствует реальному поведению, модель такой системы бесполезна. Проверка соответствия поведения модели и реальности является первым фактором валидности модели или валидности по поведению. Этот критерий используется почти всегда, но он не является единственным.

Для оценки валидности сложной системы важно проверить условия и допущения, которые используются при описании сложной системы. То есть, в какой степени предположения, используемые в модели сложной системы, учитывают и согласуются с существующими знаниями, эмпирическим опытом и научной интуицией. Иногда эмпирический опыт важнее для моделирования сложных систем, поскольку существует много ситуаций, когда теория не в состоянии описать особенности поведения сложной системы.

Степень соответствия условий и допущений определяет область применимости модели сложной системы. Поведение модели сложной системы может соответствовать реальному поведению в каких-то определённых ситуациях, которые задаются исходными допущениями. Если эти допущения не охватывают широкий спектр реальных условий, то такая модель сложной системы имеет узкое применение и по существу также не является валидной. Этот критерий валидности модели сложной системы является критерием валидности по условиям. Он показывает насколько условия, в которых применима модель, соответствуют реальным условиям функционирования данной сложной системы.

Надёжность модели сложной системы определяется тем, насколько поведение сложной системы не чувствительно к незначительным вариациям допущений модели или параметров информационной ситуации, в которой сложная система функционирует [24].

Реальные сложные системы всегда динамические. Теория динамических систем является основой большинства моделей сложных систем. Она рассматривает, как с течением времени меняются системы и их поведение. Динамическую систему можно упрощённо определить как систему, состояние которой однозначно задаётся набором переменных, поведение которых описывается предопределёнными правилами [30, с.470].

• 2.2    Метрики как характеристики сложных детерминированных систем

Для поиска метрик необходимо использовать структурно-лингвистический подход к описанию сложной системы, сущность которого состоит в детализации лингвистического подхода Холстеда с учётом структурных и содержательных особенностей сложных систем.

Между подсистемой и частью сложной системы существуют функциональные различия. Структурно они представляют собой совокупность связанных элементов, имеющих общий вход/выход. С позиций структуры при обобщенном рассмотрении система и подсистема могут быть эквивалентами. В структурном плане можно рассматривать систему как совокупность частей, элементов и связей между ними. На рисунке 3 приведены структурные элементы сложной системы. Выделено три типа качественных характеристик: части (компоненты), элементы, связи (отрезки прямых). Информационное взаимодействие между элементами основано на принципе информационного соответствия [31].

Если рассматривать систему с гетерогенными элементами, то части также можно считать элементами. Максимальное количество связей в системе, которая описывается плоским графом, равно ( n-1)n /2. Здесь n – количество связанных элементов в системе. Сложная система на рисунке 3 содержит три качественных вида характеристик.

По аналогии с метрикой Холстеда можно ввести характеристику сложности системы логической информационной длины ( iLS ) формального описания сложной системы для топологической схемы, представленной на рисунке 3.

iLS = n1 log2 n1 + n2 log 2 n2 + n3 log 2 n3 , где: iLS - логическая информационная длина формального описания сложной системы; п1 -количество разных частей системы (базис или словарь частей); n2 – количество разных элементов (Е на рисунке 3) системы (базис или словарь элементов); n3 – количество разных связей в системе (базис или словарь связей).

Выражение (6) и величину iLS можно рассматривать как первую информационную метрику сложной системы. Каждый качественный признак задаёт свой алфавит. Выражение (6) даёт одинаковое значение для систем, имеющих одинаковые словари.

Сложная система

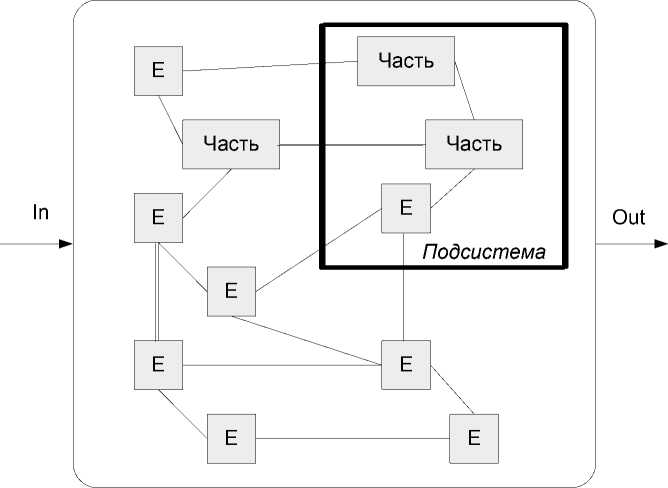
Рисунок 3 – Структурные элементы сложной системы

Определение 2 : логическая информационная длина формального описания сложной системы – это количество информации в битах, которое содержат алфавиты характеристик, описывающие данную систему.

Определение не ограничивает число видов характеристик. Поэтому в общем случае для k - характеристик сложной системы информационная логическая длина формального описания сложной системы имеет вид

• (7)    iLS = n 1 log₂ n 1 + n₂log 2 n₂ + ...+ n k log 2 n k .

Величина iLS является логической информационной характеристикой сложной системы и определяет в битах качественное содержание описания сложной системы, без учёта фактической информационной ёмкости отдельных элементов алфавита.

Логическая информационная длина является характеристикой описания системы, но не характеристикой самой системы. В аспекте закона многообразия У.Р. Эшби [26] выражение (7) является количественной характеристикой качественного многообразия. Оно может служить инвариантом описания сложных систем и сложных программ. iLS не отражает семантику и содержательную часть, а отражает только информационную ёмкость алфавитов в битах. Величина iLS является одинаковой для разных сложных систем, имеющих одинаковый набор словарей и одинаковое количество единиц в каждом словаре.

В информационных моделях и информационных конструкциях роль элементов системы выполняют информационные единицы. Фактический информационный объём в информаци- онных единицах описания конкретной сложной системы будет равен

• (8)                                  N=N1 + N + ... Nk.

Здесь N i ( i=1_k ) - число информационных единиц каждого вида, образующих данное описание сложной системы. Выражение (8) является индивидуальным для каждой системы и при этом сопоставимым для разных сложных систем с одинаковым набором информационных единиц. Оно является аналогом физического объёма. В общее число N входят и повторяющиеся единицы.

Условный объём в информационных единицах описания конкретной сложной системы определяется по аналогии с выражением (5) Холстеда по формуле

• (9)                                     V=N log 2 n .

Величина V измеряется в битах. Отдельные информационные единицы могут иметь разное количество битов. Это не отражается величиной N, которая указывает только их количество, но не учитывает информационную ёмкость каждой единицы в битах. Следовательно, величина V является условно сопоставимой только для тех сложных систем, которые имеют одинаковые алфавиты описания и используют все единицы словаря. Величина V не характеризует информативность описания системы.

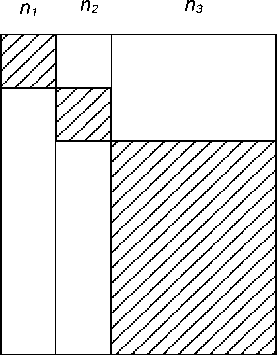
Можно использовать аналогию с теорией реляционных баз данных. Величина n характеризует универсальное отношение или строку заголовков. Величина N характеризует количество значащих строк таблицы. Величина N . n характеризует площадь таблицы в клетках, то есть произведение строк и столбцов. Площадь таблицы (аналог V ) является характеристикой объёма, но не является характеристикой информативности. На рисунке 4 приведены два примера структуры равновеликого информационного объёма для разных систем.

a

b

Рисунок 4 – Примеры структур равновеликого информационного объёма для разных систем а) и b)

Величина информационного объёма одинакова для каждой системы в вариантах а) и b). Штриховкой показаны информативные части. Особенность универсального отношения или таблицы с n столбцами в том, что значащие значения в строке имеются только для данного показателя. Например, в строке для показателя n1 будут стоять значения в столбцах, описывающих этот показатель, а в этой же строке для других показателей будут стоять нули. Такая таблица является квазидиагональной, содержащей много пустых клеток. Для вариантов a) и b) значение информационного объёма по Холстеду неизменно, но информативность таблиц для вариантов различна. Для варианта a) информативность (количество отличных от нуля значений параметров) составляет 65%V, а для варианта b) количество информативных параметров составляет 53%V. Следовательно, величина V в выражениях (5) и (9) не отражает характеристику системы, а отражает информационную ёмкость системы безотносительно к её заполнению полезной информацией.

Если рассматривать выражения (5) и (9) в аспекте информационного объёма файлов, которые их содержат, то в этом случае также можно обнаружить несоответствие. Информационный объём в битах может быть разным даже для систем с одинаковым V и равным числом n i ( i=1...k ) . Информационные единицы могут иметь разную информационную ёмкость (например, числа с обычной или двойной точностью), что в итоге приведёт к разным физическим информационным объёмам файлов, которые описывают данные системы или программы. В альтернативу выражениям (5) и (9) предлагается выражение (10), характеризующее содержательный информационный объём или содержательную информационную ёмкость ( iV ) сложной системы или программы

n

• (10)    ^iV = £ п ^х К ^х H i

i=1

В этом выражении η i обозначает информационный объём i -ой информационной единицы, величина κ - коэффициент повторяемости данной единицы в описании, величина μ – коэффициент существования данной единицы в описании (равен 1 или 0).

Выражение (10) инвариантно для систем, имеющих одинаковые словари, его можно рассматривать как вторую метрику сложной системы. Она различна для различных сложных систем, имеющих разную информативность или информативную структуру (рисунок 4). Выражение (10) содержит общую характеристику n группы систем и содержит индивидуальные характеристики системы κ и μ. Следовательно, величина iV может служить информационным инвариантом, характеризующим сложные системы и позволяющим сравнивать их между собой по критерию объёма информативности. При известных вероятностях выражение (10) трансформируется в информационную энтропию. Вторую метрику можно представить как информационный объём информативной части описания сложной системы.

Различие между (7) и (10) в том, что выражение (7) даёт приближённую оценку, а выражение (10) точную, применительно к семантике. Но при отсутствии информации о повторяемости информационных единиц или их вероятностей выражение (10) не применимо. В этом случае можно для оценки использовать выражение (7), учитывая приближённость такой оценки.

Можно расширить метрику (7) на семантические структуры. Эту метрику можно применить к семантической системе безотносительно к тому, относится она к сложным системам или не относится. По аналогии с метрикой Холстеда можно ввести понятие информационной длины или информационной ёмкости семантической системы ( iLSS ), выразив её через качественные семантические информационные единицы.

• (11)    iLSS = n 1 log 2 n 1 + n 2 log 2 n 2 + n 3 log 2 n 3 ,

где: iLSS – логическая информационная ёмкость семантической системы; n 1 – количество сигнификативных информационных единиц (базис); n 2 – количество предикативных информационных единиц; n 3 – количество ассоциативных информационных единиц. Выражение (11) можно использовать для оценки систем хранения информации.

3    Обсуждение

Холстед, вводя характеристики, заимствованные из теории К.Э. Шеннона, предложил использовать информационную сущность и ввел некие свои комбинации. В битах он измеря- ет величины, которые являются логическим описанием и не соответствуют физическому количеству битов реальной программы или реального словаря. Выражение (1) будет давать одинаковое количественное значение для разных программ, написанных на одном языке. Оно не зависит от фактической длины программы и фактического количества операторов и операндов в программе. Оно зависит от количества единиц словаря и количества словарей. У Холстеда их всегда 2. На практике их может быть больше.

Условный информационный объём программы (5) является её характеристикой, далекой от реальной информационной ёмкости или информационного объёма программы.

При построении любой модели стремятся обеспечить её простоту, валидность и надёжность [24], а также учесть когнитивные факторы построения модели: обозримости и воспринимаемости [29]. Это можно рассматривать как упрощение описания системы.

Стремление к обозримости и воспринимаемости, или к простоте, входит в противоречие с понятием сложности. Упрощение модели сложной системы может привести к искажению и исчезновению свойств, описывающих сложность. Поэтому на практике необходимо находить компромисс между попытками добиться простоты моделирования и сложностью описания модели самой системы. Поиск баланса между простотой и сложностью модели является задачей научного исследования, которую каждый исследователь решает исходя из своих критериев и особенностей объекта исследования.

Заключение

Важными задачами исследования сложных систем являются поиск баланса между простотой и сложностью для адекватного описания конкретной системы и между частным и общим для выявления общих закономерностей и инвариантов сложных систем. Теория сложных систем должна изучать их индивидуальные свойства и выявлять сопоставляемые закономерности и характеристики, что позволяет сравнивать между собой разные сложные системы и выявлять закономерности поведения однотипных сложных систем. Примером таких общих характеристик являются воспринимаемость, валидность и надёжность. Построенная модель сложной системы должна быть воспринимаема, валидна и надёжна. Инварианты, предлагаемые в данной статье, одна из попыток решения рассмотренных задач.