Межпредметные связи физики и математики в системе обучения высшего профессионального образования

Современное образование предполагает межпредметные связи, поэтому программы обучения предусматривают взаимодействие и сосуществование дисциплин в различных учебных заведениях. Междисциплинарный характер заложен в основе методологических разработок каждого предмета и является фактором эффективного усвоения материала. Кроме того, корреляция предметов в учебном процессе уменьшает дублирование информации, что значительно экономит время, формирует навыки применения общеучебных знаний на практике.

Математика, как язык естествознания, и сама физика не могут существовать изоли- рованно друг от друга, всегда развивались взаимосвязано. В школьном образовании эта преемственность четкая, продуманная и согласованная. Тем не менее, в некоторых учебных заведениях прослеживается расхождение в программах обучения, проявляемое в некорректной последовательности изучаемых тем.

Исходя из рабочей программы по физике технических направлений высшего профессионального образования, в первом семестре рассматривается классическая механика, в частности, описание механического движения, законы Ньютона, силы, законы сохранения, колебания и волны.

Таблица 1.

	Раздел 1. «Механика»
1.	Тема 1. «Описание механического движения»
2.	Тема 2. «Законы Ньютона. Силы в механике»
3.	Тема 3. «Законы сохранения в механике»
4.	Тема 4. «Механические колебания и волны»

Приведем примеры вывода формул на основе дифференциальных и интегральных исчислений.

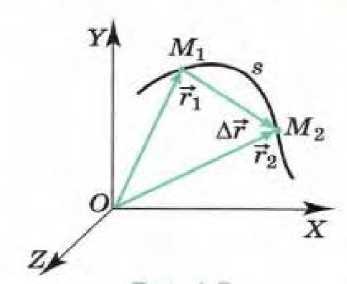
Рис. 1.

Рассмотрим алгоритм вывода формулы мгновенной скорости [1].

При движении материальной точки М радиус-вектор r изменяется с течением времени t по величине и направлению. Предположим, что материальная точка М переместилась из положения 1 в положение 2 за промежуток времени At. При этом вектор перемещения Ar = г" — r". Средний вектор скорости < и >  за промежуток

Ar времени At равен: и_ср = — .

Мгновенная скорость – это вектор скорости в данный момент времени, который определяется как предел средней скорости при At ^ 0:

, ■               , ■ Ar dr

u = lim u = lim — =

At>0 ^ср At>0 At dt

Делаем вывод о том, что скорость движения материальной точки есть векторная величина, равная первой производной радиус-вектора по времени.

В учебнике по физике 10 класса Мяки-шева Г.Я. [2] мгновенная скорость определяется через предел, но не через производную, так как производная в школьном курсе математики проходится намного позже. Это вызывает некоторые трудности у студентов при изучении данной темы. Помимо того, что им нужно вспомнить, как вычисляется производная, новой для них является ее запись. Если в школе производная обозначается с помощью штриха, то здесь появляются такие формы записи, как: —, r(t).

dt, v 7

1. мулы

Рассмотрим алгоритм вывода фор-для кинетической энергии Ек - фи- зическая скалярная величина, определяющая энергию механического движения [3].

Пусть тело массой m движется под дей ствием силы F с ускорением а = dU. Сила du

F = та, следовательно F = т —.

Так как элементарная работа этой силы

^

на перемещение dS равна dA = FdS, то ее можно записать следующим образом:

i t                .as

dA = т — dS = mdn— = mudu (2)

dt            dt

Так как по определению работа – это мера изменения энергии, то dE_k = dA. Следовательно,

J dEk = m J udr (3)

Е_к=^  (4)

Для вывода таких формул необходимы знания дифференциальных и интегральных исчислений. Если учесть тот факт, что данные темы проходят в школе и базовые знания о них должны отложиться у студентов, то никаких проблем с выводом формул быть не должно. Однако, как показывает практика, не все учащиеся помнят нахождение производных, и в особенности, вычисление интегралов. Это связанно с рядом причин.

В учебнике Мордковича А.Г. “Алгебра и начала анализа. 10 класс” на главу “Производная” выделяется 28 часов (базовый учебник) [4] или 38 часа (профильный учебник) [5]. Рассматриваются следующие темы:

Таблица 2.

Темы	Базовый учебник, ч.	Профильный учебник, ч.
1. Числовые последовательности и их свойства. Предел последовательности	1	6
2. Сумма бесконечной геометрической прогрессии	1	-
3. Предел функции	3	4
4. Определение производной	3	2
5. Вычисление производных	3	5
6. Дифференциалы сложной функции. Дифференциалы обратной функции.	-	3
7. Уравнение касательной к графику функции	2	4
8. Применение производной для исследования функции на монотонность и экстремумы	3	5
9. Построение графиков функции	3	3
10. Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке	2	6

В 11 классе к этой теме возвращаются при подготовке к ЕГЭ.

В учебнике Мордковича А.Г. “Алгебра и начала математического анализа. 11

класс” теме “Интегралы” отводятся 9 часов (базовый учебник) [6] или 13 часов (профильный учебник) [7]. Рассматриваются следующие параграфы:

Таблица 3.

Темы	Базовый учебник, ч	Профильный учебник, ч
1. Первообразная	3	4
2. Определенный интеграл	3	7
3. Контрольная работа и резерв учителя	3	2

Однако в 11 классе большой упор идет на подготовку к ЕГЭ, в котором отсутствуют задания, связанные с интегральными исчислениями [8]. Следовательно, данная тема проходится поверхностно и быстро забывается учениками.

Рассмотрим рабочую программу технического направления высшего профессионального образования. Можно увидеть, что в первом семестре проходятся такие разделы, как “Линейная алгебра” (множества и отношения, матрицы и определители, системы линейных уравнений, элементы векторной алгебры) и “Аналитическая геометрия” (метод координат, линии и поверхности второго порядка).

В начале второго семестра проходится дисциплина “Введение в математический анализ” (числовые множества, функции, пределы) и по ее завершению изучается раздел “Производная и дифференциал. Приложения производной”. Таким образом, можно заметить, что промежуток времени со сдачи ЕГЭ является достаточно большим. Уже на данном этапе можно увидеть несоответствие программ обучения по физике и математике в ВУЗе.

Половина третьего семестра математического образования у технических направлений основана на прохождении темы “ Интегральное исчисление функции одной переменной”:

Таблица 4.

	Раздел 5. «Интегральное исчисление функции одной переменной»
1.	Тема 15. «Неопределенный интеграл»
2.	Тема 16. «Определенный интеграл»
3.	Тема 17. «Приложения определенного интеграла»
4.	Тема 18. «Несобственные интегралы»

Можно сделать вывод о том, что прослеживается явное расхождение программ по физике и математике в ВУЗе у технического направления. Исправить это можно введением тем, связанных с дифференциальными и интегральными исчислениями, в первом семестре.