Microring Resonators Based on 6x6 Generalized Multimode Interference Structures using Silicon Waveguides for Photonic Applications

Published Online June 2012 in MECS

Microring resonators (MRRs) have been used as basic building blocks for optical signal processing applications such as optical switches, filters, modulators, and adddrop multiplexers [1]. Almost all of the reported works on microring resonator structures have used directional couplers as coupling elements [2]. In order to meet a variety of requirements for high-speed signal processing, the coupling coefficient needs to be adjusted arbitrarily. In general, the gap of a directional coupler can be adjusted to meet this requirement. However, for applications requiring high quality factor Q of the resonators, i.e., for high speed operation, the separations between two waveguides in the directional coupler must be very small. As a result, high loss due to conversion loss of modes is occurred [3]. In addition, the directional coupler has a large size and small fabrication tolerance. Therefore, multimode interference (MMI) couplers can be used in microring resonator structures instead of directional couplers. Use of multimode interference couplers is very attractive to the design of high speed and integrated light wave circuits due to their advantages of compactness, ease of fabrication, large fabrication tolerance and ease of cascaded integration [4].

In the literature, microring resonators based on a 2x2 and 3x3 MMI coupler was reported [2, 5, 6]; however, not much work on microring resonators based on higher order multimode interference couplers (NxN MMI couplers) using silicon waveguides have been reported. In addition, silicon on insulator (SOI) technology is considered to be a very proposing platform that has the potential to produce low lost, high index contrast, and compact devices.

Therefore, the aim of this paper is to propose a novel microring resonator structure based on 6x6 MMI couplers for the first time. The most interesting characteristic of the proposed device is that the device acts as three separate microring resonators based on 2x2 MMI couplers. The control of critical coupling of these three microring resonators can be achieved by using three separate phase shifters. The proposed device can be used for optical switching, filtering, add-drop multiplexing and sensing applications. As an example, a realization of a three-channel add drop multiplexers is presented. In addition, by choosing the lengths of the microring waveguides, a triplexer used for the fiber to the home (FTTH) networks can be achieved. The transfer matrix method (TMM) and the three dimensional beam propagation method (3D-BPM) are used to optimally design the proposed device.

The paper is organized as follows: A description of the general theory behind the use of multimode structures to achieve new structures of microring resonators is presented in Section II. Optimal design of MMI based microring resonator structures and simulation results are covered in Section III. A brief summary of the results of this research is given in Section IV.

• II.    General Theory

A Mach-Zehnder microring resonator based on 6x6 MMI couplers (MZI-MMI) is shown in Fig. 1. The two 6x6 MMI couplers have the same width W and

3L п length LMM j = —- , where L = is the beat MM 2 п Po -Pi length of the MMI coupler. In order to achieve tunable devices and control the critical coupling [7], three phase shifters Аф1, Аф2 and Аф3 are used in the three arms. Alternatively, passive phase shifters could be used to provide a desired power splitting ratio.

In order to analyze the device, the transfer matrix of the identical MMI couplers needs to be derived first and then the total transfer matrix of the device can be determined.

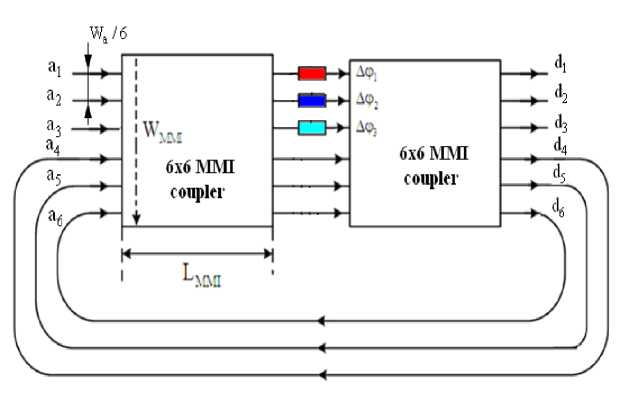
Fig. 1. Schematic of the Mach Zehnder microring resonators using 6x6 MMI couplers. Three phase shifters in three arms of the MZI are used to control critical coupling

The operation of optical MMI coupler is based on the self-imaging principle [8]. Self-imaging is a property of a multimode waveguide by which as an input field is reproduced in single or multiple images at periodic intervals along the propagation direction of the waveguide. The central structure of the MMI filter is formed by a waveguide designed to support a large number of modes. In the MMI section, the 2-D scalar Helmholtz wave equation is defined as

3L

L_MM i = 2L2 = ^_^ , the MMI coupler is characterized

by a transfer matrix M. We can prove that the overall transfer matrix S of both the MMI coupler and combiner in Fig. 1 is expressed by

d V d ² ф d x²    d y²

2 п n(x, y) X

v = P2v

M - 1

where v (x,y,z) = £ c _vv_v (x, y)exp(j( ro t - P_v z)) ; x is v = 0

the lateral dimension; y is the transverse dimension; z is the propagation direction; c is the filed excitation coefficient; y_v (x,y) is the modal field distribution; n(x,y) is the refractive index profile, v =0, 1,..., M-1 are the mode numbers of the waveguide supporting M modes; ^X is the optical wavelength and p is the propagation constant.

If we choose the MMI coupler having a length of

S = MxM = ¹

-_e ^j 4₀

- -

0 ej4

. 3п ej4

3 j4

. 3п

0     00 e

. 3п

00 e

. п.3л e4e400

. 3п.п e4e400

- п

00 e

. п

0     00 e

This matrix can be considered as consisting of three separate sub-matrices which describe four 2x2 3dB

MMI couplers, both having the transfer matrix [9]

M

2  V2

e4

. 3п e^j4

. 3п e^j4

e4

= —i=e

п j ₄

1 j

j

T 2 =

d2 a2

2      7 Аф2  „       Аф2

a₂ + cos ^2 — 2 a₂ cos _² cos 9

^АФ 2

,    _{2   2} Аф_?  „       Аф_?

1 + a 2 cos²  ^² — 2 a₂ cos —t² cos 9

^АФ 2

Relations between the complex amplitudes a , a ,..., a at the input ports and d , d ,..., d at the output ports (see Fig. 1) can be expressed in terms of the transfer matrices of the 3dB MMI couplers and the phase shifters as follows

T 3 =

d3

a3

_{2     2} Аф₃  ,       Аф₃

a₃ + cos —^-3- — 2 a₃ cos^^³- cos 9

^АФ з

,    2    2 Аф₃  „       Аф₃

1 + a₃ cos —^3- — 2 a₃ cos     cos 9

^АФ з

d1

d6

^А Ф 1

= ^{je 2}

^Т 1

*

^К 1

^К 1

*

—^Т 1

a1

a6

d2

jA£ 2 Г

= je ²

^т 2

*

^К 2

^К 2

*

—^т 2

a2

a5

Here a 1 , a ₂, and a ₃ are round trip transmissions of light propagation through the three microring resonators [6] depending the losses of light propagation from output ports d d , d back to input ports a_4, a₅ , a₅ ; for a lossless resonator a i = 1 (i=1, 2, 3) . The round trip

phases are given by: 9 1 = ^n_eff1L₁ , 9 2 = ^ n_eff2L₂ ,

d3

d 3

^d 4 J

^K 3

*

—^T 3

a3

a4

where т 1 = sin( ^1), К = cos( ^1)    ; т ₂ = sin( ^Аф 2 )   ,

K2 = cos(^2)  , T3 = sin(Аф3), K3 = cos(Аф3) ;    are coupling coefficients of the MZI-MMI couplers; Аф], Аф2, Аф3 are the phase differences between two arms of the MZI, respectively.

Using the method similar to that presented in [1], the normalized optical intensity transmitted through the proposed device are then calculated by

2 п

⁹ 3 = ~^ⁿeff3^L3

where neff1, neff2, neff3 are the effective indices of the optical mode in the ring waveguides; L1, L2, L3 are the ring circumferences (or the lengths of the microring waveguides), and X is the optical wavelength.

Therefore, the whole device can be viewed as consisting of three independent microring resonators having different coupling coefficients as shown in Fig. 2. This means that three independent switches and filters can be made by using this structure. One important and interesting characteristic of this structure applied is that the control of critical coupling for three microring resonators can be achieved separately.

T 1 =

d1 a1

a 2 + cos² ^1 — 2 a]

1              21

Аф]

cos ¹

cos 9!

2    2 Хф1_2..

1 ^i y.a  c^^s               a

Аф cos 1

cos 9 ₁

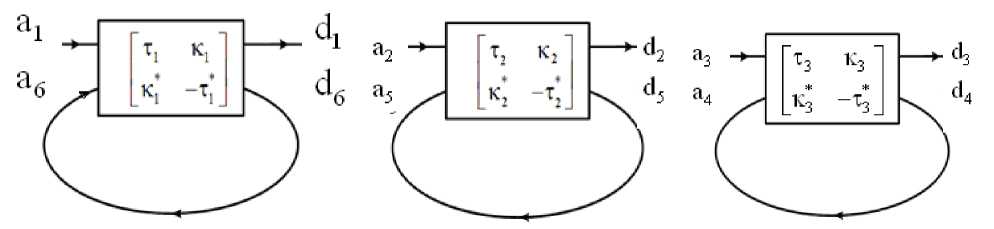
(a) MRR1                                 (b) MRR2                             (c) MRR3

Fig. 2. Three separate microresonators created from the 6x6 MMI structures

(a) microring resonator using input ports 1 and 6 (MRR1) and

(b) microring resonators using input ports 2 and 5 (MRR2) and

(c) microring resonator using ports 3 and 4 (MRR3)

Another configuration of practical interest is presented in Fig. 3, where the second MZI microring resonator structure is also coupled to the first structure. The coupling ratios can be adjusted by the phase shifters

Δϕ ₁, Δϕ ₂, Δϕ ₃, Δϕ ₄, Δϕ ₅, and Δϕ ₆ . The 12 ports of this microring resonator are referred to input ports ( E_i1, E_i2, E_i3 ), through ports ( E_t1, E_t2, E_t3 ), drop ports (E_d1, E_d2, E_d3) and add ports (E_a1, E_a2, E_a3) of

optical add-drop multiplexers.

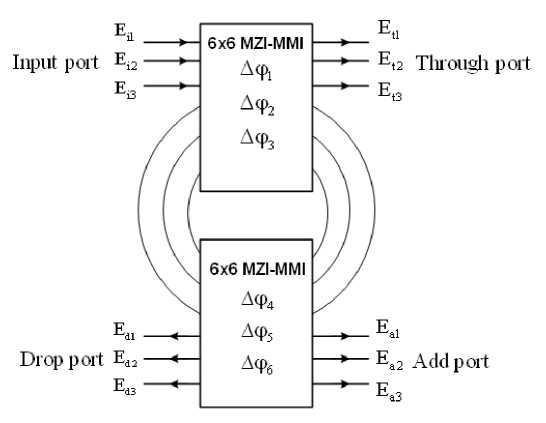
Fig. 3. Three separate add-drop multiplexers based on micro resonators using 6x6 MMI-MZI structures

The transmission powers at the output waveguides of the through ports of the add-drop multiplexers are given by

Pt1 =	Et1 Ei1	2	τ 1 1 -	- τ * 4 α 1 exp(j θ 1) τ 1 * τ * 4 α 1 exp(j θ 1)	2		(10)
Pt2 =	E t2 Ei2	2	τ 2 1 -	- τ * 5 α 2 exp(j θ 2) τ * 2 τ * 5 α 2 exp(j θ 2)		2	(11)
Pt3 =	E t3 Ei3	2	τ 3 1 -	- τ * 6 α 3 exp(j θ 3) τ * 3 τ * 6 α 3 exp(j θ 3)		2	(12)

The transmission powers at the output waveguides of the drop ports of the add-drop multiplexers are given by

^Pd1 ⁼

P d2 =

^Pd3 ⁼

E d1

Ei1

Ed2

E i2

*

-κ ₁ κ ₄

α ₁ exp(j θ ₁ /2)

**

1 - τ ₁ ^* τ ^* ₄ α ₁ exp(j θ ₁)

*

-κ ₂ κ ₅ α ₂ exp(j θ ₂ /2)

**

1 - τ ₂ τ ₅ α ₂ exp( j θ ₂)

Ed3

E i3

-κ ^* ₃ κ ₆   α ₃ exp(j θ ₃ /2)

**

1 - τ ₃ τ ₆ α ₃ exp(j θ ₃)

III. Simulation Results And Discussion

In this section, in order to verify the working principle of the devices and optimize the designs of MMI based devices, the three dimensional beam propagation method (3D-BPM) [10] is used in our study. It is well known that the finite difference time-domain (FDTD) method is a general method to solve Maxwell’s partial differential equations numerically in the time domain. Simulation results for devices on silicon waveguides using the 3D-FDTD method can achieve a very high accuracy. However, due to the limitation of computer resources and memory requirements, it is difficult to apply the 3D-FDTD method to the modeling of large devices on the silicon waveguide. Meanwhile, the 3D-BPM was shown to be a quite suitable method that has sufficient accuracy for simulating devices based on silicon waveguides [11].

The silicon waveguide structure used in the designs is shown in Fig. 4, where SiO (n=1.46) is used as the upper cladding material. An upper cladding region is needed for devices using the thermo-optic effect in order to reduce loss due to metal electrodes. Moreover, the upper cladding region is used to avoid the influence of moisture and environmental temperature.

Upper cladding

SiO; cladding

Si Substrate by using the 3D-BPM first. Fig. 5(a) shows the normalized output powers at the bar and cross ports at different MMI lengths for a signal presented at input port 1 of the MMI coupler. From this simulation result, the optimized length of MMI calculated to be LMMI = 273.5µm . The field propagation through the 6x6 MMI coupler at this optimized length is plotted in Fig. 5(b). The BPM simulations of Fig. 5(b) show that our theory has predicted accurately the transfer matrix of the MZI-MMI coupler.

Fig. 4. Waveguide structure used in our designs

The parameters used in the designs are as follows: the waveguide has a standard silicon thickness of h_co = 220nm and access waveguide widths are W = 0.48 µ m for single mode operation [12]. The refractive index of the silicon core is n_Si = 3.45 . It is assumed that the designs are for the transverse electric (TE) polarization at a central optical wavelength λ = 1550nm . The width of the MMI is to be W_MMI =8.4µm. The access waveguide is tapered to a width of W = 800nm to improve device performance.

The length of the 6x6 MZI-MMI coupler is optimized

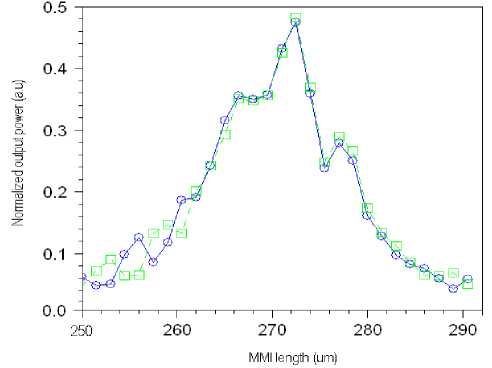
(a) Normalized output powers at different MMI lengths for input signal at input port 1 of the MZI-MMI coupler

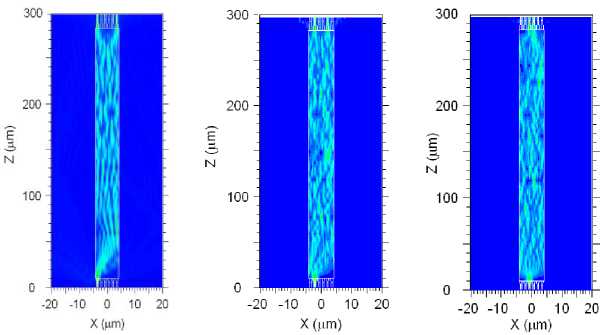
(b) Field propagation for input signal at port 1, port 2 and port 3

Fig. 5. BPM simulation results:

(a) normalized output powers at different lengths of the 6x6 MZI-MMI coupler and

(b) field propagation at the optimized MMI length for input signal at port 1, 2 and 3

The transmission spectrum of the microring resonators of Fig. 1 is shown in Fig. 6. The simulation parameters used in this study are: the width of the 6x6 MMI coupler W_MMI =8.4µm, length of the 6x6 MMI coupler L_MMI = 273.5 µ m , the lengths of microring waveguides L₁ = 700 µ m , L₂ = 800 µ m and L₃ = 900 µ m and the loss factors α ₁ = α ₂ = α ₃ = 0.98 . At this length of the MMI coupler, the microring resonators act as when the phase shifters in the MZI-MMI arms of the microring resonators are

Δϕ ₁ = Δϕ ₂= Δϕ ₃ = 0 .The most interesting characteristic of this structure is that this device can simultaneously generate the transmission spectrum of three separate 2x2 microring resonators. In addition, if phase shifters Δϕ ₁, Δϕ ₂, Δϕ ₃, Δϕ ₄, Δϕ ₅, and Δϕ ₆ are used in the MZI-MMI arms to control the coupling coefficients κ , κ , and κ , the critical coupling condition [7] can be met. As a result, devices based on the proposed structure hold the promise of wavelength-selective switching, modulation and filtering applications.

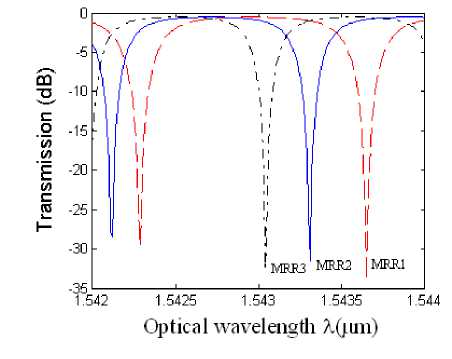
Fig. 6. Transmission spectrum of the proposed microring resonator.

The proposed structure acts as three separate 2x2 MMI based microring resonators

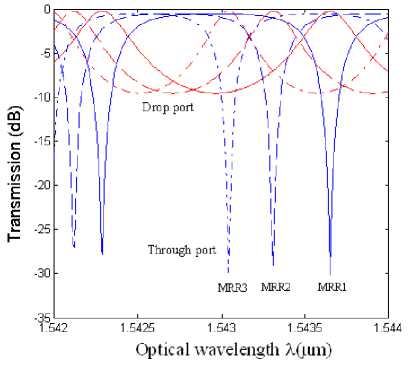
Fig. 7. Transmission spectrum of the microring resonators of Fig. 3. The proposed structure acts as three separate 2x2 microring resonator based add-drop multiplexers.

Fig. 7 shows the transmission of microring resonator add drop filters with the lengths of microring waveguides L₁ = 700 µ m , L₂ = 800 µ m and

L₃ = 900 µ m and the loss factors α ₁ = α ₂ = α ₃ = 0.98 . The simulation shows that this device can be used for implementation of a three-channel add drop multiplexer. In addition, reconfigurable add drop multiplexers

(ROADM) can also be achieved by controlling six phase shifters Δϕ ₁, Δϕ ₂, Δϕ ₃, Δϕ ₄, Δϕ ₅, and Δϕ ₆ .

Another possible application of the proposed structure is the realization of wavelength divison multiplexing (WDM) filters. Such devices are very useful in fiber to the home (FTTH) networks that provide triple-play (voice, data and video) services [13]. One of the most essential components in the FTTH networks for providing the triple-play services is the WDM filters. The WDM filter separate or combine optical signals with different wavelengths in a cost effective manner. Recently, many designs of triplexers have been proposed, including triplexer based on planar lens, gratings, multimode interference couplers, crytal photonics and cascaded MZIs [13]. However, most of the work reported is either based on low index contrast systems or directional couplers. In this study, an optical triplexer for splitting     signals     of     three     wavelengths

λ1= 1310nm, λ3= 1490nm,   λ3 = 1550nm can be implemented using the proposed structure. By setting the appropriate lengths of the microring waveguides to L1 = 105µm , L2 = 179µm and L3 = 248µm , the transmission spectrum at three drop ports of the add drop filter is shown in Fig. 8. The lengths of the microring waveguides are chosen in order to satisfy the resonance condition, where the wavelength resonance is given by mmm

λ ₁ =         , λ ₂ =         , λ ₃ =                       (16)

L 1 n eff          L 2 n eff          L 3 n eff

Here, m is an integer. It is obvious from the simulations that three separate filters having optical resonances                                         at

λ ₁ = 1310nm, λ ₃ = 1490nm, λ ₃ = 1550nm are obtained. As a result, the signal with three wavelengths λ ₁, λ ₂, and λ ₃ incoming three input ports E_i1, E_i2 , E_i3 can be multiplexed at three drop ports E_d1, E_d2 , E_d3 and the triplexer can be achieved.

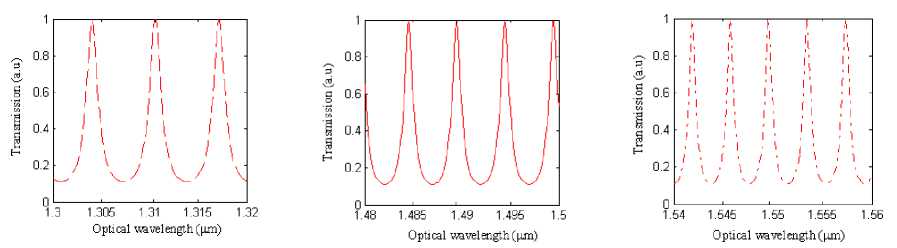
(a) MRR1, L ₁ = 105 µ m

(b) MRR2, L ₂ = 179 µ m

(c) MRR3, L ₃ = 248.3 µ m

Fig. 8. Transmission spectrum of the microring resonators of Fig. 3. The proposed structure are used for a triplexer splitting the signal of three wavelengths λ ₁ , λ ₂ , and λ ₃

• IV. Conclusion

In summary, we have presented the design of a novel microring resonator structure based on 6x6 multimode interference couplers. The proposed device generated the transmission characteristics similar to that of three separate microring resonators based on 2x2 couplers. It has been shown that the proposed device can be used for promising applications in optical communications, including switching, filtering, multiplexing and modulation. In addition, a realization of a triplexer used for the FTTH networks has been presented. Devices have been designed using silicon waveguides. The transfer matrix method and beam propagation method have been used to optimally design the device and to investigate the device performance.