Минимизация энергетических затрат в задаче оптимальной переориентации твердого тела в сопротивляющейся среде

• 1.    Постановка задачи

Уравнения управляемого углового движения твердого тела, обладающего сферической симметрией, имеют вид [1]

2X = X ° и,

I со = u - k и,

где X = ( A 0 , A 1 , A 2 , A 3 ) - кватернион, компонентами которого являются параметры Род-рига-Гамильтона A i , ° - символ кватернионного произведения, 1 1 = 1 ₂ = 1 3 = I -главные центральные моменты инерции тела, о = ( ю 1 , ю ₂ , ю ₃ ) - вектор угловой скорости, u = ( и 1 , u ₂ , и 3 ) - вектор управляющего момента, ω_i , u_i – проекции соответственно ω и u на главные центральные оси инерции, k – коэффициент аэродинамического момента сопротивления вращению тела.

Начальное положение твердого тела задается равенствами

X ( 0 ) = X o = ( A _M, A 10 , A 20 , А зо ) , и ( 0 ) = 0. (2)

В конечный момент времени T связанная с твердым телом и опорная системы координат совпадают

X ( T ) = X T = ( ± 1,0,0,0 ) , и ( т ) = 0.     (3)

На величину управляющего момента наложено ограничение и 1 + и 2 + и 3 < и 0 ,             (4)

где и ₀ = const >  0.

Требуется найти управляющие функции u_i ( t ) ( i = 1,2,3 ), удовлетворяющие ограничению (4), переводящие твердое тело из начального положения (2) в конечное (3) и доставляющие минимум функционалу энергетических затрат:

1 ^T

J = —^(и 2 + и 2 + и ₃ ² dt ,         (5)

2 0                 ³

где время перехода T задано.

В данной постановке задача рассматривалась при k _ 0 в работе [1].

2. Построение оптимального решения

u* _ uZ 1 + uZ 2 + uZ 3 ,

преобразуем соотношения (12), (13) к виду

x + kx _ u *, |u*|< 1.

Введем лам:

новые переменные по форму-

t _ —t', u0

И _ .. — и',

u = u ₀u ' ,

k _ ^lu 0 k ',

T _ — T ', J _,/ /u ₀ ' J '.

u ₀

В дальнейшем все исследования будем проводить в штрихованных переменных, однако штрихи для упрощения записи опустим. После замены (6) получаем

Преобразуем функционал (5), используя формулы (7), (9), (15):

1 ^T

J _ —J (u + u^ + u- )dt _

1 ^T                 2                   2                   2

_] [(

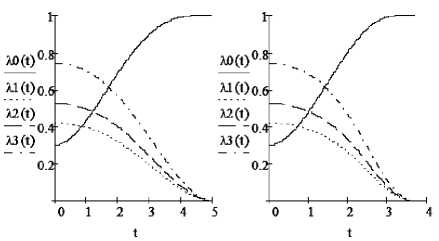
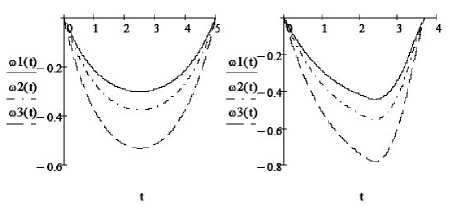
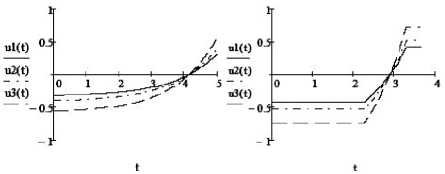
^"l [(xZ +kxZ )2+(xZ +kxZ )2+(xZ +kxZ )2 ]dt_

2X _ X ° и, ю _ u — kи, u 1 + u 2 + u 3 < 1.

TT

_ - ju*2 (z2 + Z2 + Z3)dt _ - ju*2dt.

20                       20

Тогда функционал (5) примет вид

J _¹Tu*² dt.

Вид граничных условий (2), (3) и функционала (5) останется прежним.

Решение задачи будем искать в классе плоских поворотов, при которых вектор угловой скорости ω сохраняет постоянное направление в пространстве. Тогда вектор угловой скорости может быть представлен в виде

Для объекта, описываемого дифференциальным уравнением (15), в работе [3] найдено оптимальное управление, обеспечивающее перевод фазовой точки из начального состояния x(о) _ x₀> 0, x(0) _ 0 в конечное положение x(T) _ xc(T) _ 0 и доставляющее минимум

й( t ) = x (t )z,

где Z = Z1Z2Z3) - постоянный единичный вектор, направленный по оси вращения, x – величина угла поворота.

Общее решение кинематических уравнений системы (7) при постоянном по направлению векторе угловой скорости имеет вид [2]

функционалу (16). А именно,

2 — 2ch kT + kT sh kT x0 "     k2 (ch kT — 1)     '

_x _ 1 — ch kT + ch kt — ch k (T — t)

2 — 2ch kT + kT sh kT k (T — t )sh kT

⁺ 2 — 2ch kT + kT sh kT^X0,

^x о ⁺

при

1^t

X(t) _ c ° exp — [ ю(t')dt',

*

u

_ k2 be

— J

^kT) e^h— sh kT

2 — 2ch kT + kT sh kT

x0,

где c – постоянный кватернион.

Из системы уравнений (7) следует:

2X _ i° ю + X ° u — k X ° ю.       (11)

Подставим в уравнение (11) соотношения (9) и (10). Учитывая, что Z ° Z _—1, получаем

при

J

k³x₀² shkT

min 2(2 — 2ch kT + kT sh kT);

x + kx _ uZ1 + uZ2 + u3Z3.

Из ограничения (8) вытекает

IuZ1 + uZ2 + u-з| < 1.

Полагая

2 — 2chkT + kTshkT       2, (, k

-----—,--------г----< x₀< — lnl ch—T I:

k²(ch kT — 1)        ⁰k²I 2 J

1    „ - kt

1 - e t

2--7 + xo, 0 < t < *i, kk f1 e -kt -11Z, 0 < t < T1, < k k J x = <

d 1 e ^kt +

ekt    Δ

, _л^-t^{+ d}2, ^Ti< t< ^T2^,(20)

k²Δ₁  kΔ₁

w = ^

^k(T- t >-l

⁺ — ^T 2 ^ t< ^T,

*

u =<

-1, 0 < t< Ti, 2ekt - 4    , ,

----7^2, ^Ti < t < ^T2,

Δ1       ^{1        2}

+ 1, T 2 < t< T,

J min = ^{1 (t}1^{+ T - T} 2 ^)-ТУ" ⁺A ^(t 2 - ^Ti b ⁽²²⁾ 2             kΔ₁  2Δ₁

- kde ^kt

I

(k

ekt

+-- kΔ1

e^-1

-

Δ₂

k4 J

Z, T< t< T2, ⁽²⁶⁾

Z, T 2 < t< T.

Из соотношений (7), (25), (26) определим вектор управляющего момента.

„         2 - 2ch kT + kT sh kT

^ПРИ     x° <    k 2 (ch kT - 1)    :

U = k 2 Q - e-kT )^ek - ^{sh kT}_;, 2 - 2ch kT + kT sh kT

где

при

A₁= e^kT2- e^kT1, A ₂= e^kT2+ e^kT1,

2 - 2chkT + kTshkT      2, (, k 4

-----—,--------г----< x0 < — Ini ch—T I: k2 (ch kT -1)        0 k2 I 2 J d 1 =

e^{2 kT1} + A₁ k²A₁

, d 2 =

T1(A 2 A1) ,,

+ Xf) + kA12

[- Z, 0 < t< T1,

u = (

а моменты τ₁, τ₂переключения управления определяются из следующей системы трансцендентных уравнений:

² x₀

kτ2          kτ1

+ 2 + T = 2 k^e--- 'e e^kT2- e^k

, e^{kT 2}+ e^kT1 = e^kT +1.

12t

I 4

- ⁴²I^Z, ^T1 < t< ^T2, 4 J

, Z, t₂< t< t.

Используя соотношения (2), (9), (10), получаем решение кинематических уравнений системы (7):

z =

x

- x0

где функция x = x (t) определяется равенствами (17), (20).

Неизвестную постоянную x0 и компоненты единичного вектора ζ найдем из граничного условия (3), выбирая в формулах (19), (22) из двух значений функционала наименьшее. Тогда x 0 = 2arccos| 2001,             (30)

λi0

1^{1 -}20)

λi0

1^{1 - 2}00

если 200 > 0, если 200 < 0, i = 1,3.

Покажем, что полученное решение (17), (19), (20), (22)–(31), определяющее плоский разворот твердого тела из начального положения (2) в конечное (3), удовлетворяет необходимым условиям принципа максимума Л.С.

Понтрягина [4] для задачи оптимального управления (2), (3), (5), (7), (8).

Так же, как и в работе [2], введем в рассмотрение кватернионы ψ и ϕ сопряженных переменных, в которых компоненты yi (i = 0,1, 2, 3), соответствуют параметрам Ai, а ^ (j = 1, 2, 3) - переменным a j.

Введем обозначение p = vect(~ ° у)             (32)

p = P 0^{Z.               (39)}

Тогда из (35), (37)–(39) следует, что при выполнении условия ф1²+ ф2 + ф₃²< 1:

= k₂(1 — e~kT) e — sh kT , ^Ф = * 2 — 2chkT + kTshkT^X0Z,

2k3 shkT x ,    (41)

2 — 2chkT + kTshkT⁰

и преобразуем функцию Гамильтона–

Понтрягина к следующему виду:

1³                                                   ₂

H = тЕ^(aiPi^-2ka^i+²u^i⁺?оui^).

²i=1

а при ф1²+ фI + ф₃2 > 1:

2 ek^ — ект 2 — ek ф =     kT    kT    Z ’ e 2 — e 1

P 0 = ^{2 k}

kτ ekτ2

kτ

+ e¹

При ф₀= 0 приходим к задаче оптимального по быстродействию управления переориентацией сферически симметричного твердого тела в сопротивляющейся среде, рассмотренной в работе [5]. Без ограничения общности положим ф₀= — 1.

Тогда

kτ e²

—

kτ e¹

Здесь τ₁, τ₂, x₀, ζ определяются из соотношений (24), (30), (31).

Таким образом, для рассматриваемой задачи оптимального управления переориентацией сферически симметричного твердого тела в сопротивляющейся среде решение при

H = эХ^(aiPi^{— 2ka}iVi^{+ 2и}Ф^—и ). ⁽³³⁾ 2 i =1

2arccos| A₀₀<

2 — 2ch kT + kT sh kT k² (ch kT — 1)

Преобразуем функцию H :

1³                                         2      2

H = ~^^(ai^pi^{— 2ka}i^i^—(ui^{— ф}.)⁺Vi )■⁽³⁴⁾

²i =1

описывается формулами (17), (19), (25), (27), (29)–(31); при

Из соотношений (33), (34) следует, что функция H достигает максимума при

2 — 2ch kT + kT sh kT k² (ch kT — 1)

< 2arccos| A₀₀| <

U = 5

Ф, если ф2 + ф2 + ф3 < 1, ф              2     2     2 л (35)

, если ф1 + ф2 + ^3 > 1.

U ф1

< 4ln[ ch-T] k²I 2 J

задается соотношениями (20), (22)–(24), (26), (28)–(31); при

2arccos λ₀₀

Сопряженные уравнения для системы (7) имеют вид

>-|ln (ch ^k-T ] k²I 2 J

задача решения не имеет.

2y = у ° и,            (36)

Ф = kФ ^—2P.

Из соотношений (29), (32), (36) получаем, что

V = ^0 °P0^Z° ^exP

— x0

Пример

Рассмотрим задачу оптимального управления переориентацией твердого тела из начального состояния

X(0) = (0,3; 0,4; 0,5; 0,707), и(0) = 0

в конечное положение (3) при k = 0,8.

Положим T = 5. В этом случае выполняется условие (44). Угол поворота твердого

тела за время T равен x₀= 2,532 рад., минимальное значение функционала энергетических затрат J_min= 0,792. Примем T = 3,7. В этом случае выполняется условие (45). Моменты переключения управления соответственно равны τ₁= 0,271, τ₂= 3,312.

Угол поворота твердого тела за время T равен остается прежним x0 = 2,532 рад., но при этом возрастают энергетические затраты

Jmin = 1,511.

Рис. 2. T = 3,7

Рис. 1. T = 5

Рис. 4. T = 3,7

Рис. 3. T = 5

Рис. 6. T = 3,7

Рис. 5. T = 5

Заключение