Минимизация линейной комбинации времени и энергетических затрат в задаче оптимального управления вращениями динамически симметричного твердого тела

• 1.    Постановка задачи

Уравнения управляемого вращения динамически симметричного твердого тела относительно центра масс имеют вид [1 , 2 ]

« 1 + ( I - 1 )^ з = u i , « 1 ( 0 ) = « 0 ,

• < « ₂ - ( I — 1 ) «« = U ₂ , « ( 0 ) = « 0 ,    (1)

I d ) 3 = u 3 , « 3 ^{( o )} = « 0

Здесь I = 3-, , J, J3 (J ^ J3) - главные цен- тральные моменты инерции твердого тела ( J - экваториальный, J - осевой моменты инерции), « (i = 1,2,3) - проекции вектора угловой скорости на главные центральные оси инерции, ui = ^у-, Mi (i = 1,2,3) - управляющие моменты.

Рассматривается задача гашения экваториальной составляющей угловой скорости, в конечный момент времени t = T :

« 1 ( Т ) = « 2 ( Т ) = 0. (2)

Предполагается, что функция « ( t ) является заданной функцией времени t , а управление изменением экваториальной составляющей угловой скорости осуществляется с помощью пары поворотных (верньерных) двигателей:

• u 2 + и 2 <  и 0 , и ⁰ = const >  0. (3)

2. Построение оптимального решения

Оценка эффективности управления вращением твердого тела осуществляется с помощью критерия

J = J [ 1 + k ( U + U 2 ) ] dt ,

где к >  0 и время перехода T не задано.

Требуется найти управляющие функции u 1 ( t ) , u 2 ( t ) , удовлетворяющие соотношению (3) и доставляющие минимум функционалу (4).

С помощью замены переменных щ = a cos ^ - b sin p ,

. ,                      л t \     ⁽⁵⁾

o ₂ = a sin p + b cos p , p = l ( I - 1 ) o 3 ( r ) d r

первые два уравнения системы (1) и краевые условия преобразуем к следующему виду [1, 2]:

at = щ cosp + u2 sin p, b = -щ sin p + u2 cosp,

a ( 0 ) = щ ⁰, b ( 0 ) = o₂,            (7)

a ( T ) = b ( T ) = 0.               (8)

Для решения задачи (3), (4), (6)-(8) воспользуемся принципом максимума Л.С. Понтрягина [3]. Функция Гамильтона– Понтря-гина имеет вид

H = —1 — k ( Щ + U 2 ) +

+ ( u_x cos p + u₂ sin p ) w +          (9)

+ ( - u_x sin p + u₂ cos p ) w₂ ,

если

W ^l w l' > 2 ku ⁰, то

*    0 Wi cosp - w2 sin p u = u -----.        ----

\ W1

*    0 Wi sin p + Wi cosp uQ = u ------,          -----

V ^W 1 ^{+ W} 2

Из сопряженной системы получаем

Wi = Ci, w2 = C2.(15)

Рассмотрим ситуацию, когда выполняется неравенство (11). Подставим выражения (15) в соотношения (12), а (12) - в правые части системы (6). Найдем решение данной системы уравнений, удовлетворяющее начальным условиям (7):

СС a = — t + o, , b = — t + o₂.

2 k     ¹       2 k     ²

Учитывая условия (8), вычислим постоянные C , С ₂, а затем функции a ( t ), b ( t ) :

_  2 k o i    _  2 k o 0

C i =    ^   , C 2 =    “

где W i, w₂ - переменные, сопряженные a и b соответственно.

Преобразуем функцию Гамильтона–

Понтрягина (9):

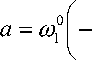
- + 1 1 , b = o ₂’(-- + 1 1. t ;         ² 1 t )

-

к u i

- к

H =- 1 + ^{W 2 + W 2}

4 k

—

-

^( W i cos p - w₂ sin

p )

-

u ₂

if-          ^1 2

^-77⁽ W i sin p ⁺ W 2 cos p )   .

2 k

Из условия максимума функции H следует, что если

W2 + W22 <2ku0,(11)

то

u * =     ( W 1 cos p - W 2 sin p ),

2k(12)

u * = —( w sin p + W ₂ cos p ) ;

2   2k    12

Так как время T окончания процесса не задано, то максимальное значение функции Гамильтона-Понтрягина H должно удовлетворять условию [4]:

H max ( t ) = H max ( T ) = 2.         (18)

Из (10), (12), (15), (16), (18) следует, что

k [ щ ⁰² + О 0 ’² I

H max =- i ■       / ----- ² = 2.     (19)

Из равенства (19) найдем время перехода из начального положения (7) в конечное положение (8):

k f o 0 ²

+ o

.

Подставляя соотношения (15), (16) и

(20) в неравенство (11), получаем, что k >                       (21)

u ⁰

Используя формулы (14)-(16),  (20)

найдем оптимальные управления u * , и 2 :

Отсюда следует, что

2 u ₁

о • о а2 sin р — а cos^

, kf а02 + а’21

С 1           Ш |         С 2         ^^2

—.     =• =--:— - —.     =• =--:— -

С-  С     и0 T С'  С     и ° T

а время окончания процесса равно

u ₂

—

а ⁰ sin р + а 0 cos p

,

T =

k f а ⁰²

+ а 02

а ° ² + а 02

u ⁰

причем

*2      *2

U + U2

При этом значении T и констант (27) функции a ( t ), b ( t ) и а ( t), а ( t ) имеют прежний

Тогда

J = 2

k I

а ⁰²

+ а 02

.

вид (17) и (25) соответственно.

Отметим, что время T , определяемое из формулы (28), совпадает с временем оптимального по быстродействию гашения эква-

ториальной составляющей угловой скорости [1, 2, 4].

Подставим соотношения (15), (27), (28) в (14) и найдем оптимальные управления

Используя выражения (5), (17), найдем угловые скорости а ( t ) и а ₂ ( t )

*

U^ , U^ :

^а 1

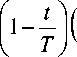
а ⁰ cos p

— а 0 sin р

*

u ₁

= и

₀ а sin р — а cos p

,

а ₂

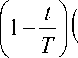
а ⁰ sin р + а 0 cos p ) ,

*

и ₂ =

—

д/ а ⁰ + а 0

О •   ,0

₀ а sin р + а cos p u

0 ²       0 ²

а + а₂

.

а затем, применяя соотношения (20), (22) и (25), получим оптимальные управления в форме синтеза

Из соотношений (17) выразим щ ⁰, н 0 через a , b и подставим полученные выражения в (29):

а к ага н ))

* u

—;

а ₂ г агат)

₀ a cos p — b sin р u ,

V a ² + b²

* 0 u ₂ = — и

a sin р + b cos p >1 a ² + b ²

Пусть теперь выполняется неравенство (13). Используя соотношения (14), (15), найдем решение системы (6), удовлетворяющее начальным условиям (7):

Воспользуемся формулами (5) и найдем оптимальные управления в форме синтеза

* _  ..0

i =— и  t y а + щ

a =

0 uС

С 2 С²

t + а ,

* 0 и = — и

^а 2

■у а + а

ь =

u С ₂

7 С ² + С 22

t + а₂ .

Вычислим значение функционала (4)

В конечный момент времени T выполняется равенство (8). Тогда

J = f1 + ки 02 ] а1

V         2

.

—

а ⁰

u ⁰ С 1

СсГСТ ’

—

®2

u ⁰ С 2

СсГСГ ■

Принцип максимума является необходимым условием оптимальности. Докажем, что найденное решение доставляет абсолютный минимум функционалу (4).

где

Введем в рассмотрение два вектора:

Z (t )=

^{a (} t )

^{b (} t )

V 4a ² ( t ) + b ² ( t ) ’ 4a² ( t ) + b ² ( t ) 7 ’ v ⁽ t ) = ( v 1 ⁽ t ) ’ v 2 ( t )) ’

v , ( t ) = u 1 ( t ) c os ^ + u ₂ ( t ) sin ^ , v ₂ ( t ) = — щ ( t ) sin ^ + u ₂ ( t ) cos ^ , причем v ² + v 2 = u 2 + u 2 . Тогда, учитывая (6), получаем

d^a ( t ) ² + b ( t ) ²

dt

= ⁽ v ⁽ t ) ^{z (} t ) ) .

Проинтегрируем это уравнение и воспользуемся краевыми условиями (7), (8):

—

ф ⁰ + ф 0

T

= J ⁽ v ⁽ t ) - ⁽ t ) ) dt .

Рассмотрим конечномерную задачу оп-

тимизации:

f ( T ) = T + k ( ф 0 ² + 2 0'2 J ^ inf,

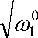
+ ф

u ⁰

— T <  0

и для ее решения применим метод множителей Лагранжа [6]. Составим функцию Ла-

гранжа

L = 2 ₀ ( T + к ⁽ ф 02

+ л

' 4 ф ² + ф о u ⁰

+ ф, ’2

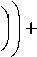
^— T

и выпишем необходимые условия локального

минимума

Тогда

0 ²       0 ²

у ф + CO 2

T

A o i '

—

k

T ²

Ф 1

+ ф

Л ₀ >  0, A >  0,

T

< J T v FW+ v lW | - ⁽ t )| ^dt =

T

= J Vu2 (t) + u22 (t) dt.

Следовательно

' 420 + ф о u “

V

)

^{— т} = 0.

22 ф 0 + ф 2

( T ,— ----- V

< JA u W+M t O dt .

V 0

Так как множители Лагранжа не равны одновременно нулю, то A 0 / 0, иначе A = 0. Поэтому без ограничения общности можно положить 2 ₀ = 1.

Тогда из соотношений (37) получаем,

Воспользуемся интегральным неравенством Коши-Буняковского [5]:

что

к I ф_х   + ф ₂

( b

J f ⁽ t ) g ⁽ t ) ^dt

V a

b

b

< J f ² ( t ) dt - J g ² ( t ) dt .

7 a

a

Пусть a = 0, b = T , f ( t ) = 1, g ( t)=Ju 1² ( t ) + u 2 ( t ) .

Тогда

ф ⁰ + ф 0

< T j ( u 2 ( t ) + u 2 ² ( t ) ) dt .      (33)

Из соотношений (32), (33) получаем

T                             0 ²       0 ²

J ( u , ² ( t ) + u 2 ² ( t ) ) dt >  ^Гф-ф- 0 ^T

.

Следовательно,

T

J = J [ 1 + k ( u + u ₂) ] dt >

0                                 (35)

. k ( 0 ² I     0 ² ^

> т + ~ I ф + ф ^ J .

к >—у  и u0

J ф ² + 2 0¹            1

т =-----7---- при к < —— .

_u 0                  _{u 0} 2

Из графика функции f = f ( т ) следует, что найденные значения T являются точками абсолютного минимума в задаче (36). Тогда из соотношений (35), (36) получаем

T

J = j [ 1 + к ( u + u2

1 при к >—- и u0

+ ф 02

J =[[1 + к ( u2 + u22)] dt >(1 + кu °2 ]        ф o                      V        7     u

1 при к < —- .

0 ² u ⁰

Следовательно,

при k >

Jmin = 2^ k ( а 102 + ®202] ,         (38) Jm  =[ ' 1 + ku °2) J а02 + а02 12 0             (39) u0 1 1 и 02 u k < 02 u соответственно, при- чем минимальные значения функционалов (38), (39) достигаются при uf, и2, определяемых равенствами (26), (30).

Таким образом, решение задачи гашения экваториальной составляющей угловой скорости динамически симметричного твердого тела описывается соотношениями (22)– (26) при k > и (25), (28)-(31) при k < ^-.

02 02

u

u

При оптимальном движении управляющий момент имеет направление, противоположное направлению вектора экваториальной угловой скорости, модуль управляющего момента ра-11

вен -^ при k > —- и равен максимальному k            _u 02

1 значению и при k < —-.

² u ⁰

В последнем случае оптимальный режим совпадает с оптимальным по быстродействию режимом гашения экваториальной составляющей угловой скорости. Время торможения и минимальное значение критерия оптимальности прямо пропорциональны модулю начального значения вектора экваториальной угловой скорости твердого тела.

Заключение

С использованием принципа максимума Л.С. Понтрягина получено точное аналитическое решение задачи оптимального управления гашением экваториальной составляющей угловой скорости динамически симметричного твердого тела.

Определены оптимальные управления в форме синтеза, угловые скорости, значение функционала качества, который характеризует в заданной пропорции расход времени и энергетических затрат.

Доказано, что полученное решение доставляет абсолютный минимум рассматриваемому функционалу.