Минимизация объемов матричного представления информации при взаимодействии автономных интеллектуальных систем

DOI:

Важным этапом при анализе ограничений на значения параметров в пространстве действий автономных интеллектуальных систем (АИС) является этап заполнения матриц зависимости параметров АИС, а также матриц ограничений параметров [1-3]. При этом объём данных, хранимых в таких матрицах, стремится к бесконечности. И тем быстрее растет объём этих данных, чем точнее представление информации, то есть, чем выше уровень дискретизации [4-6].

Ряд авторов отмечает, что это, конечно, неприемлемо для реальных приложений [7-10]. Это касается АИС на базе беспилотных летательных аппаратов (БПЛА), интеллектуальных робототехнических комплексов (ИРК), применяемых как в промышленности, так и в области точного земледелия при оптимизации транспортнотехнологических циклов БПЛА и ИРК. Очевидно, что необходимо минимизировать рост матриц с увеличением числа зависимостей и ограничений. Для этого, как правило, вводится дискретизация значений параметра и его ограничений с определенным шагом. В результате этого можно получить конечный набор значений параметра и его ограничений, что приводит к задаче минимизации объемов информации [11-13].

МАТЕРИАЛЫ И МЕТОДЫ

В целях минимизации хранящейся информации введем ограничение степени влияния значений входных параметров матрицы. При этом, получим, что, допуская определенные погрешности при формировании матрицы зависимости, имеется гораздо меньше значений параметров в каждом измерении. Известные методы [14-17] не позволяют минимизировать объем данных, хранящихся в матричной форме, в прикладных задачах, описывающих взаимодействие АИС.

Области влияния параметров

Итак, взяв матрицу размерности М х N х O , и зная, что значение входного параметра по измерению M слабо влияет на выходной параметр до определенного значения, и это значение хранится, как M , то для всех значений этого параметра меньших М_х матрица зависимости будет на одно измерение меньше, т.е. как N х O . Рисунок 1 иллюстрирует взаимовлияние параметров a, b, c .

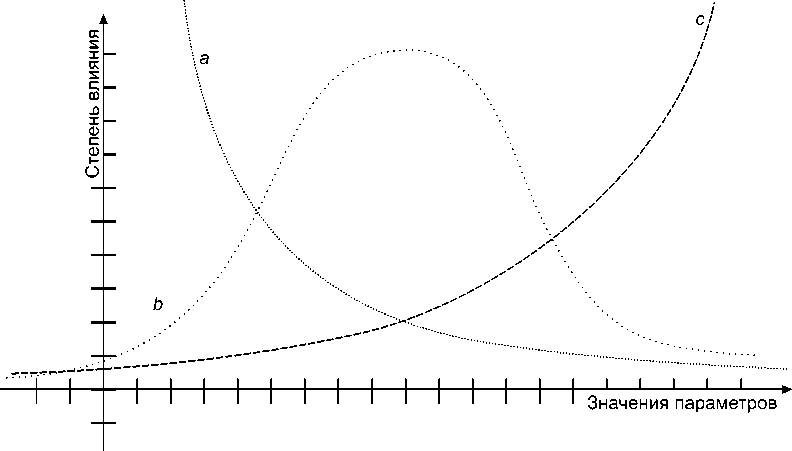
Рисунок 1. График влияния параметров: a , b , c – параметры.

Figure 1. Graph of the influence of parameters: a, b, c are parameters.

Однако, исходя из предыдущего утверждения, будет очевидно, что объём этих матриц, будет равен ( M + 1) х N х O .

Таким образом, получаем, что выделение отдельной матрицы меньшей размерности не имеет смысла. К тому же, для корректной работы с каждой матрицей необходимо дополнительно хранить информацию о списке параметров и области значений матрицы. Причем области значений не только тех параметров, которые задействованы в ней самой, но и тех, которые не учтены в ней, и не используются. Это требуется, так как необходимо отразить область значений других параметров, при которых эта матрица становится применима. Таким образом, добавляя дополнительное значение несущественного входного параметра в матрицу зависимости, мы тем самым отражаем степень его влияния на значение выходного параметра. Причем значение этого несущественного входного параметра должно лежать за пределами порогового значения штрафной функции. Это необходимо, для того чтобы при проведении интерполяции исключить случаи проверки и применения значений этого несущественного параметра, лишь применяя область его значений между значениями M и M . Так как значение M лежит за пределами порогового значения штрафа, то применяемая область будет использоваться всегда, когда значения параметра будут меньше M .

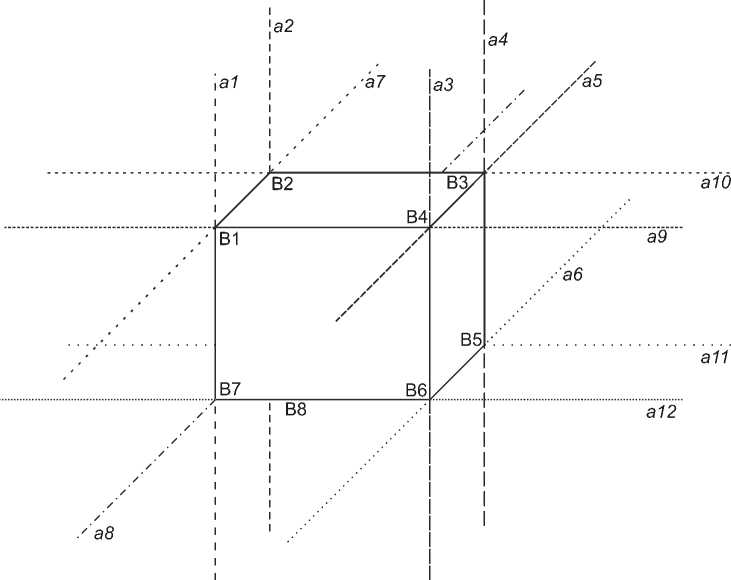
Рисунок 2. Куб значений параметров.

Figure 2. Cube of parameter values.

На рисунке 2 представлена иллюстрация значений параметров в виде куба. Внутри куба находятся значения выходного параметра, на пересечении значений входных параметров. Имеется три входных параметра. Линии, лежащие за пределами куба, иллюстрируют незначащие значения параметров, стремящиеся к M .

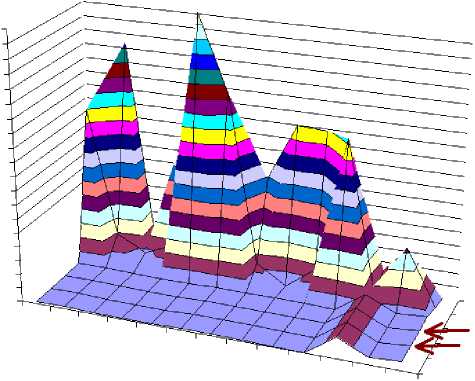
Рисунок 3. Зависимость одного параметра от двух других с двумя незначащими значениями одного параметра (помечены стрелками).

Figure 3. Dependence of one parameter on two others with two insignificant values of one parameter (marked with arrows).

Следует заметить, что в матрице зависимости краевые значения параметров, за пределами которых, параметры становятся незначащими, нужно указывать явно лишь один раз, остальные значения параметров, лежащие за пределами указанных, будем принимать такими-же, как и краевые. Это позволяет вообще отказаться от применения какой-либо интерполяции, а просто применять краевые значения параметров. На рисунке 3 представлена зависимость одного параметра от двух других, с двумя незначащими значениями одного параметра, которые помечены стрелками.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

При формировании матрицы зависимости параметра от других параметров возникает ситуация, когда параметр зависит от очень большого числа других параметров, и их число стремится к бесконечности. При работе в условиях реального мира скорость реакции системы понижается, и в конечном итоге система может заниматься вычислением значения какого-либо параметра неопределенно долгое время, так как при этом учитывается слишком большое число других параметров. Например, при добавлении в матрицу зависимости одного параметра, количество её измерений увеличивается, и объём данных таким образом увеличивается во столько раз, сколько значений имеет новый добавленный параметр. Таким образом, матрица растет слишком быстро.

Минимизация хранящейся информации в матрицах путем ограничения набора параметров

Для минимизации хранящейся информации в матрицах необходимо ввести ограничение на число параметров в матрице зависимости, сократив тем самым количество её измерений. Следует оценивать степень необходимости наличия какого-либо входного параметра в матрице зависимости по его влиянию на значение выходного параметра.

Введем понятие порога чувствительности матрицы зависимости. При некотором отклонении вычисленного значения параметра от его реального значения, не превышающем λ, изменением параметра, влияющего на такое изменение, можно пренебречь. И как отмечалось ранее, можно увеличить расстояние между точками его дискретизации, но, проанализировав все его такие значения, можно прийти к выводу, что во всех случаях его изменение не приводит к значительному изменению итогового параметра, превышающему λ.

В начале работы системы матрицы имеют очень ограниченный набор значений. В дальнейшем в ходе работы происходит коррекция значений (построение) матрицы, добавление новых значений влияющих параметров и зависимого параметра, добавляются значения и в матрицу ограничений. Таким образом, происходит «обучение» системы работе и обработке данных. Во многих случаях в ходе работы необходимо добавлять не только значения параметров, но и новые влияющие параметры в матрицу зависимости, таким образом, увеличивается размерность матрицы, что, конечно, увеличивает вычислительную нагрузку. Необходимо согласовывать изменение размерности матрицы с изменением числа значений в ней. Это необходимо для того, чтобы исключать дублирование значений как измерений, так и параметров.

Представление информации в матричном виде позволяет существенно повысить универсальность математической модели автономной системы, но приводит к некоторым сложностям как со стороны реализации определенных функций, так и со стороны оптимизаций по быстродействию. Как правило, чем больше проводится оптимизационных операций в рамках технологии хранения информации, тем менее универсальной она становится.

В то же время, применяя современные вычислительные комплексы, в которых аппаратно реализованы операции по обработке матриц, можно говорить о том, что производительность будет обеспечена на необходимом уровне.

Мы получаем задачу сохранения баланса повышения производительности и сохранения универсальности . Для ее решения предлагается ввести динамические наборы параметров для различных наборов значений с тем, чтобы в каждой области значений итогового параметра была своя матрица зависимости этого параметра от других. Тогда можно в наименее критичных случаях резко уменьшить размерность матриц и при необходимости установить её большей для повышения точности расчетов. Назовем этот процесс динамическим распределением параметров для формирования матриц зависимости по областям значений .

Для дальнейшего снижения количества значений параметров в матрице зависимости целесообразно применять различные методы интерполяции значений выходного параметра. Информация о примененной интерполяции может храниться как для всей матрицы в целом, так и для областей её значений. Это повышает гибкость применения данного метода сокращения количества значений параметров. Однако описание методов интерполяции и их применения к областям значений параметров в матрице зависимости должно быть стандартизовано и едино для всех взаимодействующих систем.

Изменение шага дискретизации

Первый наиболее простой способ по ограничению хранящейся информации – это изменение шага дискретизации в сторону его увеличения. Но так как в наборе значений одного и того же параметра могут встречаться области значений, где требуется повышенная точность вычислений, необходимо сохранять шаг дискретизации довольно маленьким, что приводит к увеличению объемов информации, хранимой в матрицах. Для того чтобы уменьшить объем информации, не влияя на точность там, где это необходимо, предлагается ввести изменяемую дискретизацию значений. В тех областях значений, где требуется повышенная точность, шаг дискретизации уменьшается до необходимых значений, а там, где в этом нет необходимости, шаг дискретизации увеличивается до значений, не приводящих к существенной погрешности вычислений.

На рисунках 3, 4 и 5 дана иллюстрация зависимости одного параметра от двух других. Но на рисунках есть существенные различия, на которых остановимся ниже.

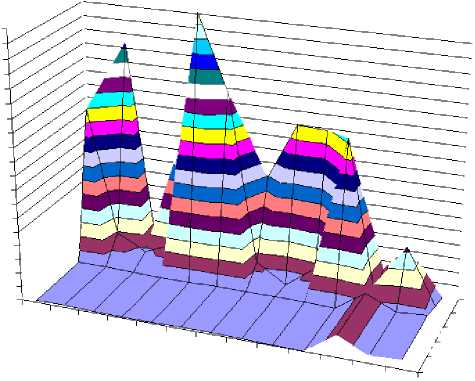
Рисунок 4. Зависимость одного параметра от двух других с двумя незначащими значениями одного параметра и с двумя отсутствующими значениями одного из входных параметров.

Figure 4. Dependence of one parameter on two others with two insignificant values of one parameter and two missing values of one of the input parameters.

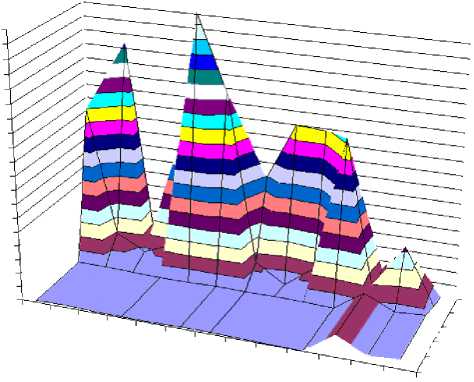
Рисунок 5. Зависимость одного параметра от двух других, с двумя незначащими значениями одного параметра с удаленными промежуточными значениями второго входного параметра.

Figure 5. Dependence of one parameter on two others, with two non-significant values of one parameter with intermediate values of the second input parameter removed.

На рисунке 3 указаны все значения параметров через определенный шаг. На рисунке 4 представлены значения параметров, с двумя отсутствующими значениями одного из входных параметров.

Для дальнейшего сокращения хранящейся информации в матрице зависимости необходимо удалить промежуточные значения второго входного параметра, что отражено на рисунке 5.

ЗАКЛЮЧЕНИЕ

Таким образом, предложен и проиллюстрирован один из возможных подходов к минимизации объемов матричного представления информации при взаимодействии автономных интеллектуальных систем. Решение задачи базируется на сохранении баланса повышения производительности и сохранения универсальности в процессе динамического распределения параметров для формирования матриц зависимости по областям значений.

Предложен метод хранения и обработки информации о параметрах интеллектуальных автономных систем, обеспечивающий оптимизацию хранящейся информации в целях минимизации её объемов. Также предложен метод хранения и обработки информации об ограничениях параметров автономных систем и разработаны процедуры минимизации объёмов информации об ограничениях.