Минимизация расхода топлива в задаче оптимального управления вращениями динамически симметричного твердого тела

1.    Постановка задачи

Уравнения вращения динамически симметричного твердого тела под воздействием малых управляющих моментов в безразмерных переменных описываются системой уравнений [1 –3 ]:

® 1 + ( I - 1 ) ® 2 ® з = £ Щ , Щ ( 0 ) = ^Ш 0 ,

• < Ш 2 - ( I - 1 ) ш 1 Ш 3 = £ U 2 , Ш 2 ( о ) = Ш 2 ,    (1)

I d ) 3 = £ U 3 , Ш ₃ ( о ) = Ш 0 , £ <<  1.

Здесь I = у3, J , J 3 ( J ^ J 3 ) - главные центральные моменты инерции твердого тела, Ш ( i = 1,2,3 ) – компоненты вектора угловой скорости, U i ( i = 1,2,3 ) – управляющие функции, £ е [ 0, £ ₀ ] - малый параметр.

Рассматривается задача гашения экваториальной составляющей угловой скорости, в конечный момент времени t = T :

Ш 1 ( Т ) = Ш ( Т ) = о.              (2)

Предполагается, что функция ш ( t ) является заданной функцией времени t , а управление изменением экваториальной составляющей угловой скорости осуществляется при помощи одного фиксированного в связанных с телом осях двигателя:

u 1 = u cos а , и 2 = u sin а ,          (3)

| и | <  и ⁰, а = const.              (4)

В работах [1, 2, 4] рассматривалась задача оптимального по быстродействию, а в работе [3] – оптимального по энергетическим затратам управления гашением экваториальной составляющей угловой скорости. В настоящей работе исследуется задача минимизации расхода топлива.

Требуется среди всех допустимых управлений и₁ ( t ) , и₂ ( t ) найти такие, для которых критерий оптимальности

T

J = £ J] u\dt ,                   (5)

где время перехода T задано, принимает наименьшее возможное значение.

• 2.    Применение принципа максимума

С помощью замены переменных щ = a cos m - b sin m, ю2 = a sin m + b cos m, t m = J(I -1)^(t)dr

первые два уравнения системы (1) и краевые условия преобразуем к следующему виду [1, 2]:

a = £ ( u , cos m + u₇ sin m ) ,

L 1   •    ,2     \(8)

b = £ ( - u 1 sin m + u 2 cos m ) ,

a(0) = щ0, b(0) = a%,(9)

a (T ) = b (T ) = 0.(10)

Для решения задачи (3)-(5), (7)-(10) воспользуемся принципом максимума Л.С. Понтрягина [5]. Функция Гамильтона-Понтрягина имеет вид принимающей

u *, u * опреде-

Используя соотношения (4), (7), (13), нетрудно убедиться в том, что выражение p cos p не может быть равным -1 или 1 на конечном промежутке времени. Таким образом, оптимальное управление u * является кусочно-постоянной функцией, значения 0, ± 1.

Управляющие функции ляются равенствами u * = u * cos a , u * = u * sin a .

• 3.    Построение усредненной системы

Для построения приближенного решения рассматриваемой задачи оптимального управления воспользуемся методом усреднения [1, 2]. Подставим u **, u * в систему уравнений (8). Усредняя по фазе m правые части уравнений, получаем

H = - £ u | + p_a £ U cos m + U 2 sin m ) + + p_b£ ( - щ sin m + u ₂ cos m ) .

Здесь p_a , p_b - переменные, сопряженные a , b . Так как функция H не зависит от a и b , то из сопряженной системы дифференциальных уравнений следует, что Р_а , Р ь = ^const.

Подставим соотношения (3) в функцию Гамильтона-Понтрягина (11) и преобразуем полученное выражение:

H = -£u| + £upcos(m- а + y), (12) где cos y = pa-, sin y = pb-, Р = VP,2 + Pb. (13) pp

Из условия максимума функции Гамильтона-Понтрягина (12), учитывая ограничение (4), найдем оптимальное управление:

0, если p | cos p | <  1,

„    u ⁰ sign cos p , если p |cos p | >  1,

• - u ⁰<  u <  0, если p cos p = - 1,

0 < u < u0, если p cos p = 1, где p = m - a + Y.(15)

£2

a = — J u *( m - а + y ) cos ( m - a ) d m ,

* ⁿ 0

£ b =--J u *(m - a + y)sin(m - a)dm.

* ⁿ 0

Используя обозначение (15), вычислим инте- гралы:

2 п

Ju*(m - a + y)cos(m - a + y)dm = p1

= 4 J u ^ocos p dip = 4 u ^osin p j,      (18)

2 n

Ju*(m - a + y)sin(m - a + y)dm =0, где p удовлетворяет равенству

1 p = arccos —.

p

Затем вычислим, используя соотношения (18), (19), интегралы в правых частях системы (17):

2 n

J u *( m - a + y ) cos ( m - a ) d m = 4 u ⁰ sin p 1 cos y ,

2 n

J u *( m - a + y ) sin ( m - a ) d m = 4 u ⁰ sin p sin y .

Тогда уравнения для усредненных фазовых переменных примут вид

2 u ⁰ sin ^

a = £----------cos y,

<           ⁿ                    (20)

b = £ ^Ain^sin y .

П

*

u =5

0, если

cos V

cos V i

< 1,

u ⁰ sign cos v , если

cos V

cos V i

> 1.

Вычислим cos v . Из соотношений (23), (24)

следует, что

4. Построение и анализ оптимального решения

cos y = -

a

=, sin y = -’ + b²

b

+ b ²

.

Найдем решение системы дифференциальных уравнений (20), учитывая начальные условия (9):

Тогда, применяя равенства (15) и (6), получаем

2 u ⁰ sin v          ₀

a = £ ---------1 cos Y t + a _x,

n

,     2 u ⁰ sin ^ .         ₀

b = £ ---------1 Sin Y t + a ₂ .

П

cos v = cos (p - a + y) = a cos a + b sin a

- cos p

—

+ b ²

Из граничных условий (10) получаем, что

•       na0

sin V i =------,

¹    2 £ u⁰ T

- sin p

—

( ⁰    .

cos y =--г, sin y = -a0

a^

0        02      02

где a = (d1 + a2

.

Воспользуемся равенствами (22), (23) образуем выражения (21):

и пре-

01          t I

a = all--I,

¹ I     T J

b = (201 1 -

t

T

.

Используя выражения (6), (24), найдем угловые скорости ( ( t ) и a ₂( t ) :

a1 =

( 1 cos p - a ₂ sin p ) ,

a2 =

( ² sin p + a ⁰ cos p ) ,

\

- b cos a + a sin a

J

\

+ b ²

J

t

(p = j(I -1)a3(r)dr.

Воспользуемся формулой (19) и преобразуем равенство (14) к виду

a 1 cos a + a ₂ sin a

y] a + a2

.

Используя соотношения найдем оптимальное управление синтеза

(26),

* u

в

(27), форме

0,

если

a cos a + a₂ sin a

I 2

yj a + a2 cos Vi

< 1,

*

u

—

u ⁰ sign ( a 1 cos a + a ₂ sin a ) ,

если

a cos a + a₂ sin a

I 2

yj a + a2 cos Vi

> 1.

Таким образом, оптимальное управление u * принимает, при выполнении неравен-

ства

a cos a + a₂ sin a

/2 . 2

у/ a 1 + a ₂ cos v 1

зависимости

от

a cos a + a sin a ; в

> 1, значения ± u⁰ в

знака

выражения

противном случае

–

u * = 0. Моменты времени, при которых происходит изменение режима оптимального

управления,

находятся

a cos a + a₂ sin a

^ a 1 + a ₂ cos v 1

из

условия

= 1, где значение cos V i

определяется из равенства (22).

Оптимальные управления u 2 , и 2 вычис ляются по формулам (16), в которые следует подставить управление и * из (28). Из соотношения (22) следует, что с увеличением заданного времени T окончания процесса увеличивается продолжительность времени вращательного движения твердого тела с выключенным двигателем ( и 2 = и 2 = 0).

В первом приближении минимальное значение функционала (5) равно

В этом случае оптимальный по расходу топлива режим совпадает с оптимальными по быстродействию и энергетическим затратам режимами гашения экваториальной составляющей угловой скорости, рассмотренными в работах [1-4]. При T = T расход топлива равен J *= г и⁰T = — ю⁰. При T <  T рассматриваемая задача решения не имеет.

5. Примеры

T

J * = £ f(|u *1 d^ ’

- среднее значение управления

и * по фазе ^ за период 2 п ,

0, если

щ cos а + щ sin а

/ Г д/ щ + а2 cos^

< 1,

u ⁰ , если

щ cos а + щ sin а щ ²+ щ cos ^ 1

> 1.

Таким образом, построенные выражения для угловых скоростей щ , о₂ из (25), функционала J * из (29), (30) и оптимальных управлений и 2 , и 2 из (16), (28) дают решение первого приближения поставленной задачи оптимального управления (1)-(5).

Интересно отметить, что в первом приближении изменение угловых скоростей щ , о₂ осуществляется по такому же закону,

Рассмотрим задачу оптимального управления экваториальной составляющей угловой скорости твердого тела для тех же числовых данных, что и в работе [3]: щ ( 0 ) = 0,5, щ ( 0 ) = 0,5Л, щ ₃ ( t ) = 0,08 1 , I = 2, г = 0,1, а = 30 ° , и ⁰ = 1.

Вычислим по формуле (31) момент окончания процесса T = 5 п (минимальное время, при котором еще возможен переход из заданного начального положения ( 0,5, 0,5д/3 ) в конечное ( 0,0 ) . В этом случае нетрудно найти, используя соотношения (23), (25), (32), точные значения точек переключения оптимального управления, и * является кусоч-

но-постоянной функцией:    и = - 1 при

t е 0, 5.

при t е 5

и и =+ 1

5 п ; расход

что и в задаче минимизации энергетических затрат, рассмотренной в работе [3].

Рассмотрим предельный случай, когда

п

^ ч- (отсутствует пассивный участок вра-

топлива равен J * = 0,5 п .

На рис. 1 изображены графики, иллюстрирующие полученное решение.

щательного движения твердого тела при и *= 0). Тогда время T окончания процесса равно

T 1 = П^ . (31) 2 г и ⁰

При этом значении T функции щ (t), щ (t) имеют прежний вид (25), а управления и2 , и2 вычисляются по формулам (16), в которых и * равно и *=- и osign 01 cos а + ®2sin а). (32)

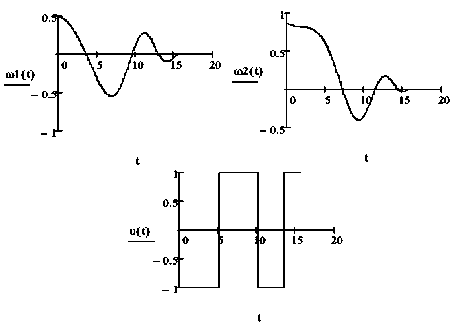
Рис. 1. T = 5 п

Положим T = 17. Для определения оптимального решения воспользуемся формулами (25), (28)–(30) и найдем угловые скорости, оптимальное управление, минимальный расход топлива.

На рис. 2 представлены графики зависимостей угловых скоростей щ, щ и управления и * от времени. Моменты переключения оптимального управления и * соответственно равны т1 = 4,046, т2 = 5,999, т3 = 9,742, т4 = 10,702 т5 = 13,170, т6 = 13,895, т7 = 15,874, т8 = 16,481.

Минимальное значение расхода топлива равно J * = 1,276.

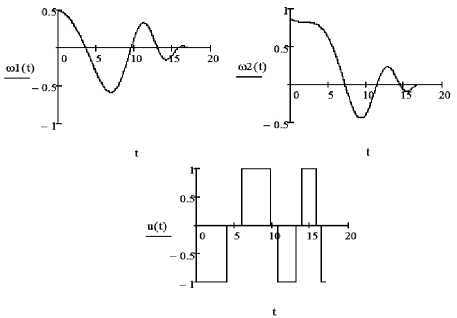
Рис. 2. T = 17

Примем T = 23. Для определения угловых скоростей, оптимального управления и расхода топлива воспользуемся соотношениями (25), (28)–(30).

В этом случае моменты переключения оптимального управления и * соответственно равны:

т1 = 2,389, т2 = 6,830, т3 = 9,178, т4 = 11,189, т5 = 12,759, т6 = 14,724, т7 = 15,535, т8 = 16,801, т9 = 17,875, т10 = 18,995, т11 = 19,960, т12 = 20,961, т13 = 21,839, т14 = 22,757.

Минимальное значение расхода топлива равно J * = 1,165.

Графики зависимостей угловых скоростей щ ( t ) , щ ( t ) и оптимального управления и *( t ) приведены на рис. 3.

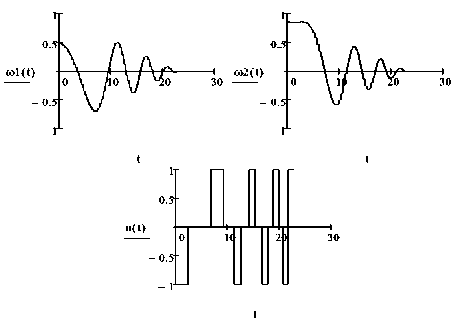
Рис. 3. T = 23

Заключение

В аналитическом виде построено приближенное решение рассматриваемой задачи оптимального управления.

Определены угловые скорости твердого тела, оптимальные управления в форме синтеза, моменты переключения управления, минимальное значение расхода топлива.

Указано условие, когда решение задачи не существует.

Представлены конкретные примеры построения оптимального решения при заданных граничных условиях.