Минимизация вырожденного квадратичного функционала на траекториях квазилинейной системы

Системы, содержащие малый параметр при нелинейных членах в правой части дифференциальных уравнений, широко используются при решении различных задач. В теории оптимального управления также есть немало работ, посвященных задачам управления объектами, описываемыми квазилинейными дифференциальными уравнениями (см. например, [1] и библиографию этой книги). Задача оптимизации квадратичного функционала на траекториях квазилинейной системы рассматривалась в [2] . В статье рассмотрим задачу оптимизации вырожденного квадратичного функционала на траекториях квазилинейной системы. Будет показано, что субоптимальным управлением, решающим эту задачу, будут управления, содержащие импульсные составляющие.

1 Постановка задачи

Рассматривается квазилинейная система дифференциальных уравнений

x ( t ) = A ( t ) x ( t ) + ^f ( x, t ) + B ( t ) V ( t).

Мы будем минимизировать вырожденный квадратичный функционал

J [ u (')l = 1 / 2

t f

У x^T ( t ) Q (t) x ( t ) dt

вдоль траекторий системы (1) . На допустимые траектории системы (1) будем накладывать граничные условия

x ( t o ) = x o , x t f = 0 .

Здесь решение системы (1) x(t) есть n-мерная функция ограниченной вариации, управление v(t) — m-мерная вектор-функция ограниченной вариации (при этом полагаем, что v(to) = 0), производные в (1) понимаются в смысле теории обобщенных функций, µ — малый параметр, to и tf —заданные начальный и конечный моменты времени, f (x,t) — нелинейная n-мерная вектор-функция, A(t) и Q(t) есть непрерывные nxn матрицы, при этом Q(t) является симметричной и неотрицательно определенной. Матрица B(t) является непрерывно дифференцируемой n x m-матрицей-функцией. Отметим, что частный случай этой задачи докладывался на конференции [5].

Как отмечалось выше, задача (1) — (3) в классе измеримых управлений решения не имеет. При ^ = 0 задача (1) — (3) рассмотрена в [3, 4] .

2 Построение вспомогательной задачи

Далее будем предполагать, что матрица B ( t) имеет структуру

—

B ( t ) =

B ( t )

где B ( t ) — m x m непрерывно дифференцируемая невырожденная матрица, 0 — нулевая ( n — m ) x m матрица. Будем обозначать первые n — m вектора x через X и последние m координат этого вектора через X. Также далее будем предполагать что вектор-функция f ( x, t ) будет зависеть не от всего вектора х, а только от его первых n — m координат, т. е.

f ( x,t ) = f 1 ( x,t ) .

Исходная задача является вырожденной и в классе измеримых функций решения не имеет. Сделаем в задаче (1) , (2) , (3) редукцию с помощью замены

y ( t ) = x ( t ) — B ( t ) v ( t ) .

Эта замена применялась при построении расширений задач оптимального управления, в частности, в [3] , [4] , [6] , [7] , [8] .

Выполняя замену (5) в задаче (1), (2), (3), получим следующую вспомогательную задачу. Требуется минимизировать функционал tf

J [ u () = 1 / 2

J [yT (t)Q(t)y(t) + 2vT (t)BT (t)Q(t)y(t)+ t0

+ v^T ( t ) B ( t)^T Q ( t ) B ( t ) v ( t )] dt                         (6)

вдоль траекторий системы дифференциальных уравнений

^{y ( t )} = ^{A ( t )} y ^{( t )} + ^^f i ^(y , t ) + B i ^{( t ) v ( t )} ,                     ⁽⁷⁾

где

B i ( t )= A (t) B ( t ) — B ( t ) , а согласно (5) и (4) f ( x,t ) = f ( y,t ) .

Краевое условие при t = t o будет иметь вид y ( t o ) = x o (v ( t o ) = 0 ) и при t = t f

y ^{( t} f ) = ^{- B ( t} f ^{) v ( t} f ) .                              ⁽⁸⁾

Учитывая структуру матрицы (5) из (8) , имеем, что первые n - m координат вектора y ( t f ) будут нулевыми. Следовательно, не накладывая никаких ограничений на y ( t f ) , условие (8) можно всегда обеспечить, полагая

v ( t f ) = - B ^{- 1} ( t f ) y ( t f ) .                            (9)

Таким образом, краевое условие x(t f ) = 0 исходной задачи во вспомогательной задаче превращается в условие y ( t f ) = 0 , а остальные координаты вектора y ( t f ) могут быть произвольными. Для исходной задачи условие (9) означает, что последние n - m координат вектора x ( t f ) будут зануляться за счет импульса в конечный момент.

Как ив [2] , при у, = 0 задача минимизации функционала (6) вдоль траекторий системы (7) будет называться базовой.

Пусть v ⁰ ( t ) , y ⁰ ( t ) — оптимальное управление и оптимальная траектория в базовой задаче (t G [ t o ,t f ] ). Согласно принципу максимума [9] существует решение сопряженной системы

^ ^{( t )} = - A T ^{( t )} ^ ^{( t )} + ^{Q ( t )}y°^{( t )} + ^{Q ( t ) B ( t ) v 0 ( t )} , соответствующее v ⁰ ( t ) , y ⁰ ( t ) , которое будем обозначать как ^ ° ( t ) . Для этого решения выполняется следующее условие:

< ( t ) B i ( t ) v⁰ ( t )- 2 v ^0T (t) B(t)T ( t ) Q ( t ) B ( t ) y ^o ( t )- v ^{o T} ( t ) B^T ( t ) Q ( t)B (t) v° ( t ) =

= max(^0T (t)Bi(t)v(t)-1 vT (t)B T (t)Q(t)B (t)y0(t)-vT (t)B T (t)Q(t)B(t)v (t). veRm

Из этого условия в предположении, что det BT(t)Q(t)B(t) = 0 Vt G [to,tf], можно найти оптимальное управление в базовой задаче v0(t) = (BT(t)Q(t)B(t))-1(BT(tW0(t) - BT(t)Q(t)y°(t)).(10)

Пусть p o = ^ ^o ( t o ) , тогда y ⁰ ( t ) , ^° ( t ) , t G [ t o ,t f ] есть решение следующей начальной задачи:

y(t) = (A(t) - M(t)BT(t)Q(t))y(t) + M(t)B1 (t)^(t),(11)

^(t) = (Q(t) - N(t)BT(t)Q(t))y(t - (AT(t) - N(t)BT№(!),(12)

где

M ( t ) = B i (t)( B ^T ( t ) Q (t) B ( t ))^-1 , N ( t ) = Q ( t ) B ( t )( B^T ( t ) Q ( t ) B ( t )) ^{- 1} . (13)

Обозначим через F ( t, s' ) фундаментальную матрицу этой системы. Эта матрица будет являться решением такой начальной задачи

F = A(t)F, F (to) = E2n, где

Ш ₌ ( A ( t - M ( t ) B T (Ж® ^{( t )} V Q ( t ) - N ( t ) B T ( t ) Q ( t )

M ( t ) B l ( t ) - ( A^T ( t ) - N ( t ) B l ( t ))

( F 11 F 12 \

F 21 F 22

Для произвольной матрицы G, содержащей n строк, обозначим через G первые n - m строк матрицы G и через G — последние m строк матрицы G. В результате матрицу перепишем в виде

^{F ( t,s} ) =

/ F ii ( t,s ) F ii ( t,s) F 2i ( t,s ) \ Fi^s)

F i2 ^{( t,s )} \

F i2 ( t, s )

F 22 ( t, s )

F 22 ( t, s )

С учетом введенных обозначений решение системы (11) , (12) можно

записать в виде

( ^{y( t )} \ Ft) F t t )

\ ^( t ) /

/ F ii ( t,t o ) F i2 ( t,t o ) \ / y ( t o ) \

F ii ( t,t o ) F i2 ( t,t o )         y ( t o )

F 2i ( t,t o ) F 22 ( t,to' )           p

\ ^F2i ^{( t,t} o ) ^F 22⁽t^,to'⁾ / \ P J

Учитывая, что y(t f ) = 0 и ^ ( t f ) = 0 , из (14) следует

( yt t o ) \ ^{y ( t} f ) \ = ( ^F ii ^{( t} f ^,t 0 ^{) F} i2 ^{( t,t} 0 ⁾ \     y t t o )

F ^{( t} f ) J \ F 2i ( t f ,t o ) F 22 ( t,t o ) J ^p

\ p )

где 0 n — нулевой n-мерный вектор. В предположении, что

F i2 ( t f , t o )

F 22 ( t f , t o )

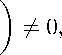
из (15) мы можем найти начальное условие для сопряженной перемен- ной p = - ( Fi2(tf,to) \-1 ( Fii(tf,to) \ ( y(to) \

V F22(tf ^o') /    V F2i(tf ,to') / \ y(to) / в базовой задаче.

3 Решение вспомогательной задачи

Теперь рассмотрим задачу минимизации функционала (6) на траекториях системы (7) . Применим принцип максимума [9] к этой задаче.

H ⁽ У, ^, v, t ) = ^ T ( AtMt ) + f ⁽ У, t ) + ^B i ( t ) ^v ( t )) - 1 / 2 ( y ^T ( t ) Q ( t)y ( t ) +

+2 v^T ( t ) B^T ( t ) Q ( t ) y ( t ) + V ^T ( t ) B ( t )^T Q ( t ) B ( t ) v ( t ) ) .

Сопряженная система будет следующей

t ( t ) = Q ( t ) y ( t ) + Q ( t ) B ( t ) v ( t ) - (а{) + fy^V^ ( t ) .    (17)

∂y

Из условия максимума функции H ( y,^,v,t ) по v получим, что экстремальное управление в этой задаче будет иметь вид (10) , т. е. совпадать с оптимальным управлением в базовой задаче. Этот факт является следствием того, что функция f i ( y,t ) не зависит от управления v.

Подставим управление (10) в (6) и (17) . Получим систему уравнений

y ( t ) = ( A ( t ) - M (t)B^T ( t ) Q ( t )) y ( t ) + fy,t ) + M ( t ) B 1 ( t ) t ( t ) ,   (18)

t ( t ) = ( Q ( t ) - N ( t ) B^T ( t)Q ( t))y (t)

- [ T ( t ) + y ( fd^ T — N ( t ) B T ( t)} t ( t ) .           (19)

Рассмотрим задачу Коши (18) , (19) с начальными условиями y ( t o ) = x o , t ( t o ) = p. При сделанных выше предположениях найдутся такие e o и µ 0 , при которых задача (18) , (19) будет иметь единственное решение y ( t,p,y ) , ^ ( t,p,y ) , t G [ t o ,t f ] при выполнении условий ||p - p o k < e o , | µ | < µ 0 .

Теорема. При сделанных ранее предположениях относительно задачи (6) , (7) при достаточно малых µ существует единственное оптимальное управление:

v°(t) = (BT(t)Q(t)B(t))-1 (BT(t)^(t,p(y),y) - BT(t)Q(t)y(t,p(y),y)) , t G [to,tf], yi(tf,p,p) = 0,i = 1,2,..., (n - m),tj (tt^p) =0, j = n - m + 1, ...,n, p(y) G Cl, p(0) = po.

Доказательство теоремы аналогично доказательству аналогичного результата в [2] и поэтому здесь не приводится.

Пользуясь алгоритмом, представленным в статье [2], продолжим изложение построения приближенного решения исходной задачи. Пусть задано натуральное число K и K < l. Так как v(») G Cl и v(0) = vq, то имеет место равенство p(») = p^K^») + o(»K), где

K

P(K Ч)) = PQ + X PkPk k=i есть полином Тейлора K-й степени. Тогда вектор-функция

V K Kt,» ) = (b^t ( t ) Q ( t ) B ( t )) ^-1 ( n ¹ ( t)^ ( t,p ^{( K}4 p),p )

-B^T ( t ) Q ( t ) y ( t,p ^{( K}4 »' ) , » ) )

будет приближенным управлением K -го порядка во вспомогательной задаче. Далее будем рассматривать процедуру нахождения коэффициентов p k , k = 1 ,...,K из разложения (18) , изложенную в статье [2] . Согласно алгоритму из [2] следует разложить левую часть уравнений

y ^{( t} f ^p) = ^{0 ,}^ ^{( t} f ,P,» ) = ^{0                   (20)}

по степеням малого параметра, применяя классическую технику Пуанкаре к системе (18) , (19) . Вектор-функции y ( t,p,» ) , ^ ( t,p,p ) в каждой точке области определения имеют частные производные по µ до порядка q включительно. Следовательно, y ( t,p,» ) и ^ ( t,p,p ) представимы в виде

K

У^Р,») = X»k Ук (t,P) + o(PK), k=Q

K

^ ^{( t,}p,» ⁾ = X »^ k ^{( t},p )+ o ⁽ » ^K ) .                ⁽²¹⁾

k =Q

Используя метод Пуанкаре, составим дифференциальные уравнения для yk (t,p) и ^k (t,p), k = 1,...,K при фиксированном p.

y o ( t,p ) = ( A (t)- M ( t ) B ^T ( t ) Q ( t )) y o ( t,p )+ M ( t ) B ^T ( t ) ^ o ( t,p ) , y o ( t o ,p ) = x q ,

4 Q ^{( t,}P ) = ^{( Q ( t ) -} N ^{( t )} B ^{T ( t ) Q ( t ))} y Q ^{( t,}P ⁾

— A(t) — N(t)BT(t) ^o(t,p), ^o(to,p) = p, yi(t,p) = (A(t) - M(t)BT(t)Q(t))yi

^{+ f} i ( Уо^ ) + ^{M ( t ) B} i ⁽ t ) ^ 1 ⁽t^,p' ) ^, y i ^{( t} Q ^,p ⁾ = ^{0 ,}

4 i ( t,p ) = ( Q ( t ) - N (t)B^T( t ) Q ( t )) y i ( t,p )-

- ( A T ( t ) — N ( t ) B T ( t ) ) ^ 1 ( t,p ) - ( fy^ T ^ o ( t,p ) , ^ 1 ( t o ,p ) = 0 , (22)

y 2 ^{( t,}p ) = ^{( A ( t ) -} M ( t ^- B^T ( t ^{- Q}(:^t' ^-- У 2 (t’P ^- + ^{df 1 ( y0A}t ^- y ₁ ^{( t,}p ⁾+ ∂y

+M(t)B1 (t)^2(t,p), , y2(t0,p) = 0, ih(t,p) = (Q(t) -N(t)BT(t-Q(t--y2(t,p) - (AT(t) - N(t-BT(t)) ^1(t,p)-

-( ^{df 1 (}y ⁰ ’^t) ) ^T ^ i ( t,p ) - ^ ^T ( t,p ) - ( ^dfy^y i ( t,p ) , ^ 2 ( t o ,t ) =0 и так далее.

Из приведенных выше систем (22) видно, что нахождение коэффициентов в представлениях (21) при заданном p сводится к последовательному решению начальных задач для систем линейных дифференциальных уравнений. В силу (21) левая часть уравнения (20) предста- вима в виде

K

Rfa^ = X P k ^R k ⁽ P ⁾ + ^{o (} ^ K ⁾ .

k=1

Здесь R k ( p ) = y k ( t f ’P ) k = 0 , ...,K. Составим системы линейных уравнений для векторов p k , к = 1 , ...,K. В соответствии с алгоритмом, изложенным в [2] , применим здесь метод неопределенных коэффициентов. Разложим в ряд вектор-функцию P K =1 P k R k ( P k )( p— по степеням p до порядка N . Затем приравняем коэффициенты разложения. В результате получим следующие невырожденные системы линейных уравнений для последовательного нахождения векторов V k , к = 1 ,...,N :

∂R 1

^F 12 ^{( t} 0 ’t f ⁾ P 1 = ^{- R} 1 ⁽ P 0 ⁾ ’ F 12 ^{( t} 0 ^,t f ⁾ P 2 = ^{- R} 2 ⁽ P 0 ⁾--dp ⁽ P 0 ⁾ P 1 ’ ... ⁽²³⁾

Для построения правых частей этих систем необходимо знать значения функций y k ( t,p) и их частных производных по компонентам вектора p в точке ( t o ,p o ) . Искомые значения получаются в результате интегрирования уравнений (22) . Начальные задачи для производных получаем в результате дифференцирования этих же уравнений. Приведем пример для производной функции y 0 ( t, p ) :

d ∂y 0 dt ∂p

d ∂ψ 0 dt ∂p

A ( t ) д о + BMP ^{- 1} ( t ) B 2 ( t ) ^ ’  . (< « ) = 0 ’

Q(t)dp + [Q(t)B^P-1(t)B2(t) - AT(t)]dp0’ d? (to) = E ∂p

При вычислении правых частей систем (22) должны выполняться равенства y o ( t,v o ) = y ^o ( t ) , ф o ( t,v o ) = ф^ ) , t G [ t o ,t f ] . Тогда R i ( v o ) = y ^o ( t f ) , а вектор-функции y ⁰ ( t ) , ф у фф являются решениями задачи:

y i ( t ) = A ( t ) y i ( t ) + f i (-Mt ) ,y o ( t ) ,t) + B i ( t ) P ^{- 1} ( t ) B ₂ ( t ) ^ i ( t ) , y i ( t o ) = 0 ,

Ф i ( t ) = Q ( t ) y i ( t) + [ Q ( t ) B ( t ) P ^-i ( t ) B ₂ ( t ) - A T ( t )] ф 1 ( t )-

^{- d}h ⁽ ^ 0 ⁽^,У 0 ^{( t ) ,t )} , ^ i ^{( t} o ) = ⁰ . ∂y

В результате последовательного решения системы (22) находим p k , к = 1 , ...,N и строим полином p ^{( N}Чц)- Управление v ^N( t, ц ) является приближенным управлением N -го порядка во вспомогательной задаче. Теперь необходимо решить задачу при p = p^{( N} Чц)- Тогда

^(t,v(N Чц)ц = Ф^)(t, ц) + o(^N), где

N

Ф^4t,P ) = X ц ^к ^ k ^{( t )} , t ^{G [ t} o ^,t f ^] .

k=o

Величины ^ k ( t ) определяются путем последовательного решения задач Коши, отличающихся от (22) только начальными условиями для ф k : ф k ( to) = V k , к = 0 ,..., N . Управление

v ^(N Ч^ц ) = ^{P - i ( t ) B}2 ^{( t),}/ ^N \фц\ t ^{G [ t}o^,t f ^{]          (24)}

вместе с V N Ч^ц ) является приближенным управлением N -го порядка во вспомогательной задаче. Так как ф ⁾ ( t,ц ) = Ф° ( Ф ) , t G [ t o ,t f ] , то v ⁽⁰⁾ ( t,ц ) = ^( t ) является решением базовой задачи и приближенным управлением нулевого порядка во вспомогательной задаче. Аппроксимация управления первого порядка представимо в виде:

v ⁽¹⁾ ( t,ц )= P ^{- i} ( t ) B 2 ( t)^ ^o ( t ) + ц ( ф 1^l ( t ) + F 22 ( t,t o ) v i )) , t G [ t o ,t f ] .

Коэффициенты полиномов, с помощью которых строятся приближенные управления, зависят от начального состояния исходной системы. При построении приближенных управлений нулевого и первого порядка эта зависимость будет учтена. Далее будем считать, что выполнено условие det F i2 ( t f ,t o ) = 0 при всех to < t f . Момент t f будем считать также заданным. Из формулы (16) следует, что

P o ⁽ y^^,t o ⁾ = ^{- F}i₂⁽t f ,to)F ii ^{( t} f ^,t o ⁾ yo.

Согласно (24) имеем

v ⁽⁰⁾ ( t,y o ,t o )) = P ^- 1 ( t ) B 2 ( t ) ^ ( ^O) ( t,y o ,t o ) , t € [ t o ,t f ] .

А так как ^ (0) ( t o , y o , t o ) = p o ( y o ,t o ) , то

u ^(o) ( t o ,y o ,t o )) = P ^- 1 ( t ) B 2 ( t ) v o ( y o ,t o ) .

Поскольку (yo,to) — произвольное начальное состояние, то вектор-функция vW(y,t) = -P    - и,. - i 2 f ,t)Fu(tf ,t)y представляет собой оптимальное управление типа обратной связи в базовой задаче. Для всех t < tf справедливо равенство F(tf ,t) = G(t), где матрица

G ( t ) =

G ii ( t ) G i2 ( t ) \

G 21 ( t ) G 22 ( t )

является решением краевой задачи

G = - GA ( t ) , G ( t f )= E ,n .

Поэтому асимптотически субоптимальная обратная связь нулевого порядка может быть записана в виде

v ⁽⁰4 y,t ) = - P ^{- 1} ( t ) B 2 ( t ) G - 1 ( t ) G ii ( t ) y.

Асимптотически субоптимальная обратная связь первого порядка представима в следующей форме:

v(14y,t) = -P-1(t)B2(t)G-21(t)Ri(y,t), где

t f

Rifat ) = y i ^{( t} f ^,y^{,t )} = J ⁽ G 11 ^{( T ) f ( u,}C i ^{( T,t )} y^,T ) ^-

^{- G} 12 ^{( t} ) Jh ⁽ C 1 ^{( T}, tfa C 2 ^{( т}, tfa ^T )) d^T, ∂y

C 1 ^{( t,t} 0 ⁾ = ^F 11 ^{( t,t} 0 ^{) —} F 12 ^{( t,t} 0 ^{) G}12 ^{( t} 0 ^{) G} 11 ^{( t} 0 ⁾ , C 2 ^{( t,t} o) = F 21 ^{( t,t} 0 ^{) —} F 22 ^{( t,t} 0 ^{) G -} 2 ^{( t} 0 ^{) G} 11 ^{( t} 0 ⁾ .

Последовательно будет построено субоптимальное управление вспомо- гательной задачи v(N)(y(t),t).

4 Субоптимальное управление в исходной задаче

Для построения субоптимального решения исходной задачи нужно продифференцировать полученное решение вспомогательной задачи в смысле теории обобщенных функций. Учитывая, что v(N)(y(t),t) = 0 при t < to, дифференцируя функцию v(N)(y(t),t), получим субоптимальное управление для исходной задачи. Оно будет иметь вид vn(t) = AtoVN(to,x(to),^(t-to')+vNr>(t, P) + Atf VN(tf, x(tf ),p)S(t-tf ),

(25) где 6 ( t ) — дельта-функция Дирака.

В (25) первое слагаемое A _t 0 v n ( t o ,x ( t o) , ^ ) определяет интенсивность импульсного воздействия, реализуемого в начальный момент, которое обеспечивает начальный скачок траектории. Слагаемое vj N ( t, ^ ) является непрерывной функцией и осуществляет управление системой на интервале ( t o , if ) • В конечный момент управление с помощью импульса сделает нулевыми последние n - m координат фазового вектора.

Управление (25) является программным. Переход к позиционному алгоритму управления приведет к появлению импульсно-скользящих режимов [10] .

Заключение

В работе предложена рекуррентная процедура построения субоптимального управления. Особенность задачи состоит в том, что искомое управление имеет импульсные составляющие. Сначала строится вспомогательная задача, решение которой существует в классе кусочно непрерывных управлений. С помощью решения вспомогательной задачи строится субоптимальное решение исходной задачи.