Многокритериальная оптимизация технологических параметров СВЧ-выпечки сбивного бездрожжевого бескоркового хлеба

В настоящее время приоритетным направлением технической политики агропромышленного комплекса является разработка системы перспективных мер по насыщению высококачественной продукцией в низком ценовом сегменте и эффективной техникой. С этой целью необходимо разрабатывать и внедрять инновационные технологии и технологическое оборудование для выпуска хлебобулочных изделий повышенной пищевой ценности и низкой себестоимости. Для внедрения ускоренной безд-рожжевой технологии хлебобулочных изделий наиболее проблемной является стадия выпечки с позиции высоких энергозатрат [1].

Актуальным является применение эффективных источников подвода энергии к тестовым заготовкам для снижения энергозатрат и продолжительности, повышения качества в процессе выпечки сбивных бездрожжевых хлебобулочных изделий.

Существуют различные механизмы подвода или генерации тепла, вызывающего интенсивный нагрев выпекаемой тестовой заготовки: способы (радиационно-конвективные), при которых тепло к выпекаемой тестовой заготовке подводится из вне; способы (электроконтактный; в электрическом поле высокой и сверхвысокой частоты; инфракрасного нагрева), при которых тепло выделяется в массе прогреваемой тестовой заготовки [2, 3]; способы с комбинированным прогревом (высокочастотный с инфракрасным; в электрическом поле токов высокой частоты с инфракрасным; инфракрасный с электрокон-тактным; инфракрасный с ультразвуком).

При применении интенсивных физических способов подвода тепла к тестовым заготовкам необходимо учитывать формирование высокого качества сбивных бездрожжевых хлебобулочных изделий. Выпечка является заключительной стадией приготовления хлеба, в ходе которой окончательно формируется его качество. В процессе выпечки внутри тестовой заготовки одновременно протекают микробиологические, биохимические и коллоидные процессы, в основе которых лежат физические явления – прогревание тестовой заготовки, влагообмен между тестом и паровоздушной средой пекарной камеры, внутренний тепломассообмен между мякишем и коркой хлеба [4].

Ввиду равномерности прогрева тестовой заготовки по всему объему и экономичности данного процесса, при выпечке сбивного бездрож-жевого бескоркового хлеба наибольший интерес представляет сверхвысокочастотный нагрев [5].

Одним из методов изучения процесса выпечки хлеба является метод математического моделирования, основным этапом которого является формализация математической модели. В настоящее время сформировались два подхода к построению математических моделей процесса выпечки [6].

Первый подход заключается в построении детерминированной модели выпечки на основе фундаментальных теоретических законов тепло и массообмена в сопряженной постановке. При этом могут быть учтены фазовый переход, механизмы капиллярной, молекулярной диффузии, термодиффузии, многофазное течение в пористой среде (вода, пар, углекислый газ) [7–11]. В ряде случаев в математических моделях учитывается давление в газовой фазе и реология мякиша, изменение геометрических размеров заготовки в ходе выпечки, цвет корки, пористость заготовки и другие параметры [10–12].

Второй подход – экспериментальностатистический, использующий концепцию «чёрный ящик» и не требующий формального описания закономерностей протекания реальных процессов при выпечке. Математическая модель в этом случае имеет вид регрессионных зависимостей, полученных в результате статистической обработки экспериментальных данных пассивных или активных экспериментов.

В лабораторной практике при исследовании технологических процессов пищевых производств наиболее эффективными являются активные эксперименты (планирование эксперимента), основной целью которых является получение максимума информации об объекте моделирования при минимальном объеме экспериментальных исследований [13].

По результатам планирования эксперимента математическая модель изучаемого процесса имеет вид полинома второй степени [13, 14] nn  n y=ь + уьх + уьх2 + Ykx.x, ,  (1)

0                i i                ii i                  ij i j i=1                i=1                 i, j=1

i * j где yˆ – предсказанное значение выходного параметра (функция отклика); b , b , b , b – регрессионные коэффициенты; X – кодированные значения факторов; i, j – индексы факторов; n – число факторов.

Цель работы – исследование взаимодействия основных технологических факторов, влияющих на процесс СВЧ-выпечки сбивного бездрожжевого бескоркового хлеба, математическими методами планирования эксперимента, и поиск оптимальных параметров процесса СВЧ-выпечки.

Результаты

В качестве основных факторов, влияющих на процесс СВЧ-выпечки сбивного бездрожже-вого бескоркового хлеба, были выбраны: x 1 – масса тестовой заготовки, г; x 2 – мощность СВЧ-выпечки, Вт (таблица 1).

Таблица 1.

Характеристики планирования

Table 1.

Planning characteristics

Условия планирования | Planning conditions	Значения факторов | Values of factors
	Масса тестовой заготовки х 1 , г The mass of the test piece x 1 , g	Мощность СВЧ-выпечки х 2 , Вт Microwave baking power x 2 , W
Основной уровень (0) | Main level (0)	350	700
Интервал варьирования | Variation interval	100	200
Верхний уровень (+1) | Upper level (+1)	450	900
Нижний уровень (-1) | Lower level (-1)	250	500
Верхняя «звездная» точка (+1,41) | The upper "star" point (+1.41)	491	982
Нижняя «звездная» точка (-1,41) | The lower "star" point (-1.41)	209	418

Все эти факторы совместимы и некоррелированны между собой. Выбор интервалов изменения факторов обусловлен технологическими условиями производства сбивного хлеба. Мощность СВЧ менее 400 Вт не обеспечивает прогрев и выпечку хлеба, так как температура в центре мякиша не достигает температуры 98±1 ºС. При этом выбор массы тестовой заготовки обоснован известным развесом хлеба.

В качестве выходных параметров использовали: y 1 – продолжительность выпечки хлеба до его готовности, мин; y 2 – упек хлеба, %; y 3 – изменение высоты хлеба после выпечки, мм.

Выбор данных параметров обоснован тем, что готовность хлеба судят по достижению температуры в центре мякиша – 98±1 ºС, выход хлеба судят по его упеку, пористость хлеба оценивают по изменению высоты тестовой заготовки в процессе выпечки изделия.

Моделирование и оптимизацию параметров СВЧ-выпечки проводили экспериментальностатистическими методами в несколько этапов [16].

Первый этап заключался в построении математических моделей, адекватно описывающих зависимости выбранных выходных параметров от изучаемых факторов. С целью сокращения продолжительности экспериментальных исследований и снижения затрат на их реализацию был выполнен полный факторный эксперимент (ПФЭ) типа 2³ в соответствии с матрицей планирования (таблица 2, опыты 1–4). Опыты проводили в двух кратной повторности, для оценки воспроизводимости опытов в центре плана были реализованы 5 параллельных опытов (таблица 2, опыты 9–13). Число опытов в центре плана выбрали с учетом возможного в дальнейшем перехода к планированию второго порядка. Для исключения влияния неконтролируемых параметров на результаты эксперимента порядок опытов рандомизировали посредством таблицы случайных чисел. В таблица 2 представлены средние арифметические значения функций отклика по результатам двух параллельных опытов.

Таблица 2.

Матрица планирования и результаты эксперимента

Table 2.

Planning matrix and experiment results

Опыт Experiment	Кодированные значения Coded values		Натуральные значения Natural values		Функция отклика Response function
	Х 1	Х 2	х 1 , г х 1 , g	х 2 , Вт x 2 , W	y 1 , мин y 1 , min	y 2 , % y 2 , %	y 3 , мм y 3 , mm
1	-1	-1	250	500	4,6	2,2	51,0
2	+1	-1	450	500	5,2	2,1	79,2
3	-1	+1	250	900	2,7	6,0	51,0
4	+1	+1	450	900	3,5	1,5	77,2
5	-1,41	0	209	700	3,0	5,15	53,4
6	+1,41	0	491	700	4,0	1,62	82,0
7	-1,41	0	350	418	6,2	1,42	63,5
8	0	-1,414	350	982	2,7	2,9	61,8
9	0	+1,41	350	700	4,0	1,95	63,5
10	0	0	350	700	4,1	2,31	63,0
11	0	0	350	700	3,8	2,0	63,8
12	0	0	350	700	3,9	2,1	62,9
13	0	0	350	700	4,0	2,0	63,1

План ПФЭ типа 2² дает возможность рассчитать оценку четырех регрессионных коэффициентов уравнения (1) и построить уравнение первого порядка. Как известно [14, 16], свободный член b 0 уравнения регрессии является оценкой выхода процесса в центральной точке эксперимента, которая смешана с суммарной оценкой квадратичных эффектов всех факторов. Если квадратичные эффекты будут значимы, то и прогнозируемые результаты опытов в центре плана эксперимента будут значимо отличаться от их экспериментальных значений. Параллельные опыты в центре плана эксперимента позволяют, не приступая даже к расчету всех (кроме b 0 ) оценок коэффициентов уравнения, судить о возможности описания изучаемых зависимостей уравнением первого порядка без включения в него квадратичных членов.

Расчеты показали, что уравнения регрессии, полученные по результатам ПФЭ, дают неудовлетворительное математическое описание и необходимо перейти к планированию второго порядка, что позволяет учесть в регрессионных уравнениях оценки квадратичных эффектов факторов.

Для этого в исходную матрицу планирования были включены опыты в «звездных» точках (таблица 2, опыты 5–8). Выбор величины «звездного» плеча ± 1,41 обусловлен необходимостью получения униформ-ротатабельного плана, обеспечивающего получения одинаковой величины дисперсии предсказания для любой точки в пределах изучаемой области [17, 18]. Опыты в «звездных» точках реализовали в двухкратной повторности. В таблица 2 представлены средние арифметические значения функции отклика в двух параллельных опытах.

Статистическая обработка экспериментальных данных заключалась в вычислении оценок регрессионных коэффициентов, проверке их значимости, оценке воспроизводимости опытов и установлении адекватности полученных регрессионных уравнений [16, 18]. При этом были использованы статистические критерии Стьюдента, Кохрена и Фишера (при доверительной вероятности р = 0,95 и соответствующем числе степеней свободы) [14, 15].

В результате статистической обработки результатов планирования эксперимента (таблица 2) получены уравнения регрессии, адекватно описывающие зависимости функций отклика от изучаемых факторов

• У, = 3,97 + 0,35 X. - 1,06 X, +

• 1                        1             2      ;(2)

+ 0,05 XX ₂ - 0,23 X 2 + 0,23 Х₂

• У , = 2,08-1,19X + 0,66X -212

• - 1,1 XX + 0,68 X 2 + 0,08 Х 2 ’

У з = 63,57 + 11,95 X - 0,66 X ₂ -

• 3                           1             2    ;(4)

• - 0,27 XX + 1,76 X 2 - 0,75 Х 2

где X – кодированные значения факторов, которые с учетом условий планирования (таблица 1) связаны с натуральными значениями XI соотношениями v _ x - 350, v _x2 - 700

-X "1                      ;   -X-

• ¹     100       ²      200

  
  

Второй этап заключался в интерпретации регрессионных уравнений (2)–(4).

Математическое описание, полученное по результатам ротатабельного планирования, дает информацию о поверхности отклика, однако, интерпретация регрессионных уравнений в виде (2)–(4) затруднена. В этой связи для идентификации вида поверхностей отклика и приведения регрессионных уравнений к канонической форме воспользуемся средствами аналитической геометрии [19, 20].

Приведение квадратичного уравнения регрессии вида (1) к канонической форме заключается в замене старых координатных осей X 1 и X 2 новыми осями Z 1 и Z 2 , переносе начала координат в новую точку факторного пространства и повороту координатных осей на некоторый угол ф [15, 20].

После канонических преобразований регрессионные уравнения (2)–(4) приобретают вид у = 2,98 + 0,23Z2 - 0,23Z22;(6)

y2 = 1,62 +1,01 Z2 - 0,24Z22;(7)

Уз = 43,31 +1,76Z2 - 0,75Z22.(8)

Графическая интерпретация регрессионных уравнений (2) – (4) в виде линий равного уровня представлена на рис. 1–3. Видно, что все поверхности отклика имеет вид гиперболических параболоидов с особой центральной точкой (точкой минимакса). В направлении одной из канонических осей существует минимум, в направлении другой оси – максимум. При этом двумерные сечения гиперболического параболоида координатными плоскостями y = h (где h - произвольная постоянная) имеют вид гипербол.

Там же на рисунках 1–3 представлены двумерные сечения области эксперимента в виде окружности радиусом R = 1,41 , центр которой совпадает с центром эксперимента.

Третий этап заключался в определении оптимальных значений массы тестовой заготовки и мощности СВЧ-выпечки, при которых достигаются экстремумы функций отклика: у ^ min , Уз ^ min и y ^ max .

Видно (рисунки 1–3), что оптимальные значения выходных параметров y 1 , y 2 и y 3 достигаются в разных точках факторного пространства. Так, y ₁ ^mn = 2,49 мин при X ** =- 1,11 и X * = 0,87;   y ₂min = 1,17  % при   X * = 1,12  и

X * = 0,85; y ₃max = 84,21 мм при X 2 = 1,41 и

X ₂ =- 0,077. Очевидно, не представляется возможным установить оптимальные значения переменных X 1 и X 2 , доставляющих экстремум трем параметрам оптимизации y 1 , y 2 и y 3 одновременно.

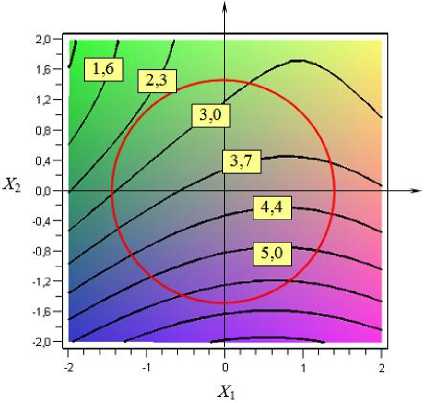
Рисунок 1. Двумерные сечения поверхности отклика y ₁

Figure 1. Two-dimensional sections of the response surface y ˆ

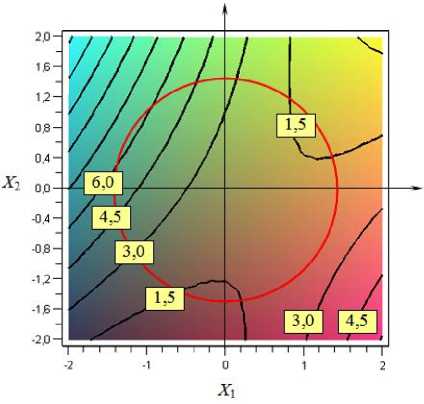
Рисунок 2. Двумерные сечения поверхности отклика y ₂

Figure 2. Two-dimensional sections of the response surface y ˆ

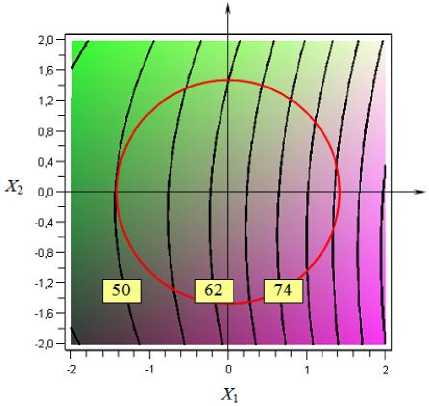
Рисунок 3. Двумерные сечения поверхности отклика y ₃

Figure 3. Two-dimensional sections of the response surface

Рассматриваемая задача оптимизации является многокритериальной с конфликтом между оптимальными значениями переменных X 1 и X 2 и по каждому частному параметру оптимизации. Для ее решения воспользуемся методом свертывания частных критериев в обобщенный аддитивный критерий F [21]

n

F =xay’ (9) i=1

где i – порядковый номер частного критерия оптимизации, n – количество частных критериев оптимизации, n = 3); a. - весовой коэффициент (0 — a - 1) относительной важности частного критерия y ˆ ; y – нормированное значение частного критерия оптимизации.

Поскольку установить приоритет по важности для каждого частного критерия оптимизации затруднительно, весовые коэффициенты a назначим исходя из значений коэффициентов относительного разброса частных критериев.

Коэффициент относительного разброса S i , характеризующий крутизну поверхности отклика, для каждого частного критерия оптимизации

S =

max     min max

y i = 1, n

max min где y , y – соответственно, наибольшее и наименьшее значение i-го частного критерия, рассчитанные по уравнениям (2) – (4) для области эксперимента (таблица 3).

Таблица 3.

Расчет весовых коэффициентов

Table 3.

Calculation of weight coefficients

Частный критерий оптимизации y i A particular optimization criterion y i	Наибольшее значение частного критерия y imax Highest value of a particular criterion y imax	Наименьшее значение частного критерия y imin Smallest value of a particular criterion y imin	Коэффициент относительного разброса δ 1 Relative spread coefficient δ 1	Весовой коэффициент α 1 Weight factor α 1
y 1	5,65	2,49	0,559	0,316
y 2	6,04	1,17	0,806	0,457
y 2	84,21	50,36	0,399	0,226

Весовые коэффициенты а связаны с коэффициентами относительного разброса S соотношением

S а = -—, i =1, n.          (11)

Xs

i = 1

Рассчитанные значения весовых коэффициентов частных критериев оптимизации представлены в таблица 5.

Для приведения частных критериев yˆ к безразмерному виду y использовали соотношение yi = yilyfma , i = 1, n . В результате нормировки уравнения (2)–(4) принимают вид y = 0,702 + 0,0619X. -0,1876X. +

1                              1                 2        ; (12)

+ 0,0088 XX - 0,0407 X 2 - 0,0407 X²

y. = 0,345 - 0,1981 X + 0,109 X. -

• ^{2                            1               2}     ,   (13)

• - 0,182 XX + 0,1139 X ² + 0,013 X²

y₃ = 0,7549 + 0,1419 X - 0,00783 X₂ -

• ^{3                              1                  2}    , (14)

• - 0,0032 XX + 0,0209 X ² - 0,0088 X²

• ¹².    (15)

Тогда обобщенный критерий оптимизации F по форме (9) определится как средневзвешенная сумма нормированных частных критериев (12) – (14)

F = - 0,2074 + 0,103 X + 0, 007431X. +

+ 0,0796 XX - 0,0344 X ² - 0,0208 X²

При формировании обобщенного критерия оптимизации F для минимизируемых частных критериев y_z , i = 1, 2 , весовые коэффициенты а приняты со знаком «-»; для максимизируемого критерия j) i , i = 3 , коэффициент a i принят со знаком «+».

Графический анализ линий равного уровня обобщенного критерия оптимизации (15) показал (рис. 4), что максимум функции F расположен на удалении от области эксперимента, границы которой определяются уравнением

X 2 + X 2 = R ², (16) что в факторном пространстве представляет собой сферу с центром в центре эксперимента и с радиусом R = 1,41 [16].

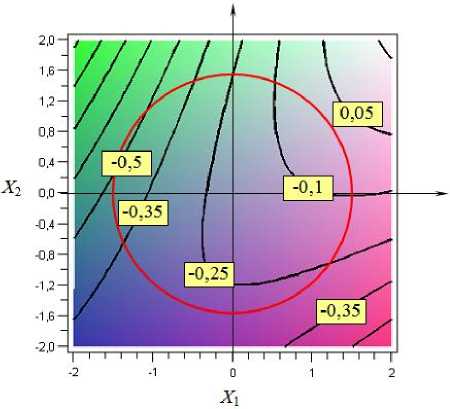
Рисунок 4. Линии равного уровня обобщенного критерия оптимизации F

Figure 4. Lines of equal level of the generalized optimization criterion F

F = - 0,2074 + 0,103 X_x + 0,007431 X ₂ + + 0,0796 XX - 0,0344 X 2 -          (17)

• - 0,0208 X 2 + X ( X 2 + X 2 - R ² ) .

Необходимым условием безусловного экстремума функции Лагранжа является равенство нулю частных производных функции (17) по всем независимым переменным Х 1 , Х 2 и неопределенному множителю X

---= 0,103 + 0,0796 X ₂ -

5Xi

• -    0,0688 Х + 2 Х Х, = 0;

SF

---= 0,007431 + 0,0796 X. -

• 5 X2

• -    0,0216 Х ₂ + 2 Х Х_г = 0;

• —    = X 2 + X ₂² - R ² = 0.

ax     12

В этой связи, оптимизационная задача сводится к нахождению экстремума обобщенного критерия оптимизации (15) F ^ max при наличии ограничения (уравнения связи) (16). Для решения поставленной задачи условной оптимизации воспользуемся методом неопределенных множителей Лагранжа [22, 23], который позволяет задачу на условный экстремум свести к безусловной задаче поиска экстремума функции.

Для этого составим вспомогательную функцию Лагранжа F , представляющую собой аддитивную свертку уравнения (15) и уравнения связи (16), умноженного на неопределенный множитель Лагранжа X

Решая систему уравнений (18) относительное переменных Х 1 , Х 2 и множителя Лагранжа X при R = 1,41 , получаем значения X и координаты стационарных точек факторного пространства X ^* и X ^* , в которых достигается условный экстремум обобщенного критерия оптимизации F (15) (таблица 4). Нетрудно убедиться, что координаты каждой экстремальной точки удовлетворяют уравнению связи (16). Там же в таблица 4 представлены значения *

частных критериев оптимизации y_t , i = 1, n , рассчитанных по уравнениям, соответственно, (2)–(4) в стационарных точках.

Таблица 4.

Результаты оптимизации

Table 4.

Optimization results

Точка Point	X 1 *	X 2 *	X	F *	* y 1 , min	* y ˆ2* , %	* y , mm
1	-0,23	-1,395	0,016	-0,258	5,81	1,27	60,46
2	0,47	-1,332	0,037	-0,263	5,87	1,62	69,477
3	-1,265	0,629	0,094	-0,459	2,54	1,243	50,956
4	1,148	0,825	-0,039	-0,067	3,398	1,174	78,47

Проверка достаточного условия существования экстремума, показала, что стационарная точка факторного пространства с координатами X * = 1,148 и X * = 0,825 является точкой условного максимума обобщенного критерия оптимизации F =- 0,067 (таблица 4).

Переходя от кодированных значений факторов к натуральным с учетом характеристик планирования (таблица 1), получим оптимальные значения массы тестовой заготовки х ** = 464,8 г и мощности СВЧ-выпечки х₂ = 865,0 Вт, обеспечивающих максимум обобщенного критерия оптимизации.

Заключение

Определены оптимальные значения основных факторов (массу тестовой заготовки – 465 г., мощность СВЧ-выпечки – 865 Вт), обеспечивающих наименьший упек хлеба – 1,2 % и максимальную высоту хлеба – 78,5 мм при минимальной продолжительности выпечки хлеба – 3,4 мин.

Экспериментальные исследования процесса выпечки сбивного бездрожжевого безкоркового хлеба, проведенные в условиях лаборатории «Региональный научно-исследовательский центр инновационной технологии хлебопечения» на базе хлебозавода № 7 г. Воронежа, подтвердили оптимальность рассчитанных по предложенной методике режимов выпечки.