Многообразие запутанности как характеристика составных квантовых систем: случай двух кубитов

В настоящее время запутанность рассматривается как основное отличие квантово-механических систем от классических, делающее первые интересными с точки зрения приложений в вопросах обработки информации и квантовых коммуникаций. Ряд авторов указывают на запутанность как на основную причину ускорения квантово-механических расчетов по сравнению с классическими [2].

В области квантовых вычислений на физическое явление запутанности утвердился взгляд как на особый информационный ресурс, сравнимый по важности с энергией. Прилагаются большие усилия, направленные на углубление понимания этого физического явления, однако законченной теории запутанности в настоящее время не создано. Актуальными направлениями исследований являются:

• -    создание универсальных мер запутанности, приложимых не только к чистым, но и смешанным состояниям;

• -    изучение свойств многокомпонентных квантовых систем;

• -    вопросы взаимосвязи различных мер запутанности.

В настоящей работе вопросы, связанные с запутанностью смешанных состояний, нами не обсуждаются.

Одним из важнейших свойств запутанности, играющим важную роль в дальнейших рассуждениях, является инвариантность запутанности по отношению к локальным операциям над подсистемами квантовой системы [1; 3]. Другими словами, запутанное состояние двух и более кубитов не может быть ни создано, ни существенно изменено (в смысле изменения запутанности) воздействием только на отдельные кубиты. Таким образом, все состояния, которые могут быть получены из состояния с заданной запутанностью только с помощью локальных операций, можно отождествить в смысле величины хранимой в них запутанности. Возникает вопрос о том, как устроено множество таких состояний? Обладает ли оно структурой многообразия, и если да, каковы геометрические свойства этого многообразия? В случае двух кубитов простой подсчет параметров, описывающих состояние полной системы (шесть вещественных параметров), и параметров, описывающих каждый кубит по отдельности (по два вещественных параметра), показывает, что, если оно существует, то это – поверхность (два параметра) в пространстве, вообще говоря, пятнадцати измерений.

Многообразие запутанности

Следующие простые рассуждения демонстрируют, что многообразие запутанности всегда существует для составных квантовых систем и является особенностью, отличающей их от классических.

Сначала сделаем замечание по поводу связности гильбертова пространства состояний квантовой системы. Действительно, любое допустимое состояние квантовой системы может быть переведено в любое другое неким унитарным преобразованием. Кроме того, унитарное преобразование, мало отличающееся от единичного, переводит произвольное квантовое состояние в соседнее, мало отличающееся состояние. Таким образом, любые два состояния квантовой системы можно связать непрерывным путем.

Предположим, мы имеем некое состояние квантовой системы. Применим всевозможные локальные унитарные преобразования к подсистемам и отождествим полученные таким образом состояния. Теперь применим к любому из полученных состояний унитарное преобразование общего вида, при этом мы либо изменим его запутанность, либо нет. В последнем случае это может означать либо то, что преобразование общего вида случайно оказалось локальным преобразованием, и мы остались в том же множестве отождествленных состояний, либо оно оказалось симметрией искомого многообразия запутанности. Последнее означает, что мы оказались в некоем состоянии, которое может быть достигнуто и другим, непрерывным, путем, в силу связности пространства состояний. Таким образом, можно считать, что всегда применено преобразование общего вида, меняющее запутанность. В результате повторения данной процедуры все пространство состояний будет покрыто на непе-ресекающиеся множества состояний с одинаковой запутанностью. Выбирая по одному состоянию как представителю из подпространств отождествленных состояний и заботясь о том, чтобы они могли быть переведены друг в друга унитарным преобразованием, мало отличающимся от тождественного, получим гладкое многообразие, которое и будет искомым многообразием запутанности.

Эта идеология применима без существенных изменений к случаю произвольного количества кубитов с той оговоркой, что многообразие запутанности организовано тем сложнее, чем большее количество кубитов в квантовом регистре. В нем будут выделяться отдельные подмногообразия, соответствующие запутанности двух, трех и т. д. подсистем, вплоть до состояний, в которых запутаны все подсистемы. Таким образом, многообразие запутанности доставляет естественную меру запутанности, связанную со структурой этого многообразия.

Неформально мы можем определить многообразие запутанности как любое множество состояний квантовой системы, имеющих разную запутанность и взятое с точностью до локального преобразования. Более точно многообразие запутанности определяется как фактор-пространство состояний полной системы S по состояниям подсистем S_k

E s = HH s 1 ® H s 2 ® ••• ® H sk , (1) где H_s – гильбертово пространство полной системы;

H_sk – гильбертовы пространства состояний k -й подсистемы.

Для n кубитов получим, соответственно:

E n = H n / H 1 ® H 1 ® ••• ® H 1 ,                            (2)

где H_n – гильбертово пространство квантового регистра;

H ₁ – гильбертовы пространства каждого из кубитов.

В общем случае для n кубитов размерность многообразия описывается формулой dim(En) = 2(2n – n – 1).                                     (3)

Следует заметить, что два соседних состояния полученного многообразия могут иметь и одинаковую запутанность, но не быть отождествленными, так как класс преобразований, не изменяющих запутанность, вообще говоря, более широкий, чем класс чисто локальных унитарных операций.

Группа преобразований многообразия запутанности n -кубитного регистра, связывающая две произвольные точки многообразия E_n , получается как фактор-группа G = U (2 ⁿ )/ / U (2) ® U (2) ® ••• ® U (2).

Вопросы морфинга данного многообразия в пространстве состояний полной системы под действием группы локальных преобразований в настоящей работе нами не рассматриваются.

Случай двух кубитов

В применении к случаю двух кубитов мы исходим из параметризации произвольного состояния системы, выбранной в следующем виде:

созхоС°8Х1 e ^° гф1

cosxosinxi e-1№+vi

IVO =                      . .

8ШХ0С08Х2 e+,¥:fl ^

^sinxosinxa e"1"1*’0"1"1*’2 ^

которая введена по аналогии с параметризацией кубита

И =

cos^ e ^гф sinx e^+iV>

Унитарное преобразование кубита U можно параметризовать, например, так:

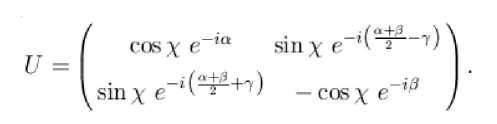
На сфере Блоха это преобразование генерирует вращение вектора r :

r' = Mr,

представимое матрицей M следующего вида:

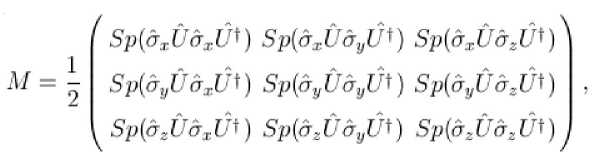
где о i - матрицы Паули.

Учитывая тождество

U 1 ® U 2 = ( U 1 ® I ) ( I® U 2 ),                               (9)

будем производить унитарные преобразования над каждым из кубитов в отдельности. Для этого перепишем состояние двух кубитов следующим образом:

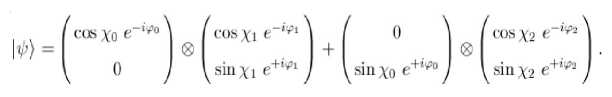
В качестве преобразования U ₂

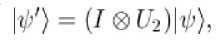
выберем преобразование, компенсирующее произвольное значение «долготы» кубитов ф 1 и ф ₂. Это преобразование всегда существует из геометрических соображений и сводится к вращению сферы Блоха вокруг оси, задаваемой вектором

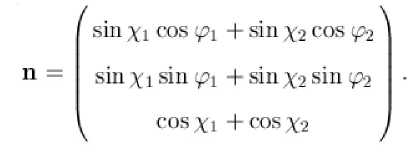
При этом преобразование претерпевают и «полярные» углы кубитов

X1 ^ X‘1, X2 ^ ^2,

в дальнейшем штрих опускаем.

Для применения преобразования U ₁ перепишем состояние кубита следующим образом:

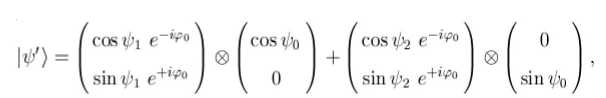
где введены новые полярные углы, связанные со старыми следующим образом:

cos Ф о cos Ф 1 = cos X o cos X 1 , cos ф о sin V i = cos X 2 sin X o , sin ф о cos V 2 = sin X i cos X o , sin V o sin V 2 = sin X 2 sin X o .

В качестве преобразования U ₁ выберем комбинацию поворота вокруг оси z , компенсирующего полярный угол ф ₀, и поворота сферы Блоха, зануляющего один из полярных углов

Фо ^ 0, X2 ^ 0, Xi ^ (xi - Тл) ^ X1.

В результате получим состояние вида:

W") =(LWW

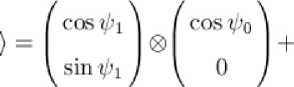
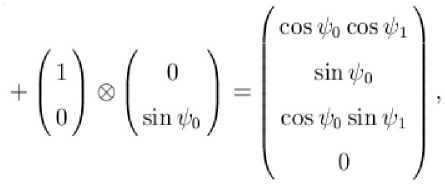
которое и описывает искомое многообразие.

Видно, что найденное многообразие является поверхностью в трехмерном пространстве, так как одно измерение в ходе преобразований естественным образом выпадает.

Полученное многообразие описывается двумя параметрами, поэтому при фиксированной величине запутанности оно будет распадаться на одномерные слои с одинаковой запутанностью. Подробное исследование геометрических свойств многообразия запутанности и его подмногообразий, а также обобщение предложенного подхода на смешанные состояния предполагается выполнить в ближайшее время.