Модель накопления повреждений в ортотропном композиционном материале

В процессе эксплуатации конструктивные элементы силового оборудования, например, газотурбинных установок, которые находят применение от самолетов до многочисленных промышленных производств, могут подвергаться как циклическому усталостному нагружению, так и случайным воздействиям, в том числе динамическим. Случается это вследствие нерегламентированного использования инструмента во время ремонта и обслуживания, попадания посторонних предметов (камней, птиц и другого), а также влияния температурного режима. При создании конструктивных элементов часто применяются композиционные материалы. Для оценки их эксплуатационных характеристик необходимы обоснованные теоретические и экспериментальные подходы, поэтому прибегают и к физическому (натурному), и математическому моделированию поведения в условиях, приближенных к эксплуатационным. Для численного моделирования задач деформирования и разрушения элементов конструкций из композиционных материалов необходимы определяющие соотношения и математические модели на их основе, способные адекватно описывать поведение композиционного материала с учетом внешних факторов: скорости нагружения, температуры, вида напряженно-деформированного состояния, а также структурных изменений, обусловленных накоплением поврежденности. Широкое распространение получили феноменологические определяющие соотношения, вид и параметры которых устанавливаются по результатам квазистатических, в том числе циклических, и динамических испытаний композиционных материалов (стандартных видов деформирования при растяжении, сжатии, изгибе, сдвиге и другом). Далее они включаются в модели для численных расчетов, а по полученным данным прогнозируется поведение реальной конструкции, а затем проводится верификация базирующихся на них моделей. Обычно верификацию проводят путем сопоставления результатов натурного испытания образца и численного (конечно-элементного) расчета его дискретного аналога.

Слоистый композиционный материал характеризуется как сложный объект, изучение деформирования и разрушения которого возможно на различных масштабных уровнях. На нижнем (микроскопическом) уровне композит считается гетерогенной средой, которая состоит из армирующих элементов (наполнителя) и окружающей матрицы (связующего). При использовании метода конечных элементов на микроуровне предполагается дискретизация отдельных элементов композита, напряжения и деформации для которых

оцениваются отдельно, при этом решаемая задача деформирования гетерогенной среды достаточно ресурсоемка. На макроскопическом уровне (макроуровне) композиционный материал представляется как сплошная среда с некоторыми осредненными (эффективными) свойствами. Математическая модель такой среды должна учитывать в процессах деформирования и разрушения факторы, проявляющиеся на микроскопическом масштабе, а именно расслоения, трещины, разрушение отдельных элементов композита и связи между ними. В случае, когда при рассмотрении композиционного материала возможно выделение некоторой повторяющейся структуры, например, монослоя (в слоистом композите) или ячейки периодичности (в тканном композите), то свойства композита можно моделировать на промежуточном, так называемом мезоструктурном уровне. На этом уровне анализируются структуры, отличные от структур образующих его элементов (наполнителя и связующего).

Эффективным подходом для решения задач деформирования и разрушения композиционных материалов в настоящее время служит прямое компьютерное моделирование. Существующие численные методы решения задач, в которых оценивается деформационное поведение композитов, учитывают как физическую, так и геометрическую нелинейность. Популярным численным методом является метод конечных элементов (МКЭ). МКЭ обладает общностью аппроксимации конечных элементов и формулировок разрешающих уравнений. Для задач статики часто применяется неявная по времени схема интегрирования, а для динамических задач более эффективна явная схема интегрирования, с помощью которой адекватно описываются различные нелинейные эффекты и волновые процессы, имеющие место при изменяющихся нагрузках. По этой причине МКЭ реализован в большом числе коммерческих программных продуктов и имеет обширное практическое приложение.

Современные пакеты прикладных программ конечно-элементного моделирования (ANSYS [1] , SIMULIA ABAQUS [2] , COMSOL Multiphysics [3] ) позволяют в какой-то мере реализовать двухуровневый подход при рассмотрении слоистых композитов, но в полном объеме учет причин и механизмов разрушения они не осуществляют. Указанные программные комплексы также дают возможность встраивать в конечно-элементный анализ пользовательские модели деформирования и разрушения материала. Так, в пакет ABAQUS включена пользовательская функция (VUMAT для явного решателя или UMAT для неявного решателя), которая дает возможность находить реакцию материала по сформулированным в инкрементальной форме для каждого шага нагружения определяющим соотношениям. Аналогичный подход встроен в ANSYS, когда требуется привлечение пользовательских моделей. Программный пакет COMSOL Muliphysics предоставляет подход для явного использования физических соотношений, например, для системы дифференциальных уравнений общей постановки (General Form PDE) или ослабленной постановки (Weak Form PDE). Масштабные факторы и механизмы деформирования на мезоскопическом уровне в этом подходе учитываются несколькими путями: явно записываются определяющие соотношения, содержащие физические и геометрические нелинейности, или в расчет принимается прямая модель поведения представительного объема на более низком масштабном уровне (подсеточная модель).

Следует отметить, что в настоящее время развиваются российские аналоги программных продуктов конечно-элементного анализа, например, EFES (г. Томск) [4 –7] и CAE-Fidesys (г. Москва) [8 –10] , которые также позволяют рассматривать гетерогенные среды на разных структурных уровнях. Интенсивно развиваются подходы к моделированию эффективных упругих свойств композитов, в которых учитываются, например, микроструктура [11 –15] , пористость [16] . Разрабатываются модели разрушения представительного объема (или ячейки периодичности) композиционных материалов [17 –19] . Также следует назвать работы, посвященные многоуровневому моделированию композитов [20] , в том числе стохастической природы их внутренней структуры на различных масштабных уровнях [21] .

Актуальным является развитие моделей деформирования и разрушения представительного объема (ячейки периодичности как повторяющейся структуры) композиционных материалов, накопление повреждений, разные механизмы разрушения (разрушение матрицы или армирующих волокон, отслоение, деламинация) в широком диапазоне деформационных и температурных воздействий. Поэтому цель данной работы заключается в создании такой структурно-феноменологической модели представительного объема ортотропного композиционного материала, которая учитывает накопление повреждений. При этом важная роль отводится верификации модели на основе экспериментальных исследований деформационного поведения композиционных материалов при квазистатических, динамических и циклических нагружениях в совокупности с методами непрерывной регистрации физико-механических характеристик, в том числе с учетом накопления повреждений.

• 2.    Учет накопления повреждений в твердом деформируемом теле

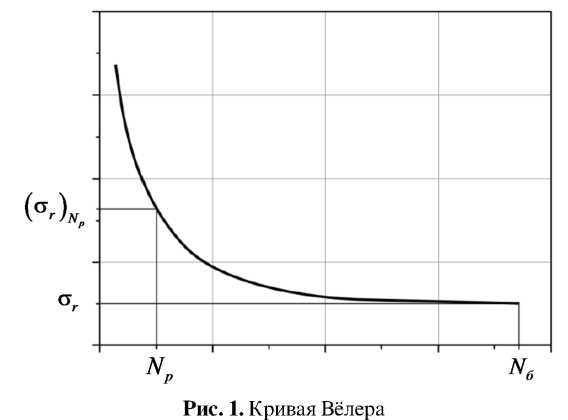
Накопление повреждений в конструкционных металлах и сплавах при квазистатическом и циклическом воздействии — один из важных аспектов их изучения. При этом усталостное разрушение трактуется именно как постепенное накопление повреждений в материале в результате воздействия переменных (циклически повторяющихся) нагрузок. Процесс накопления повреждений является кумулятивным и необратимым, приводящим к деградации механических свойств материала, возникновению и накоплению микроповреждений с дальнейшим зарождением микро- и макротрещин. Многоцикловая усталость материалов характеризуется числом циклов нагружения, превышающим 105. На каждом цикле нагружения полагается, что макроскопически образец деформируется упруго, но несмотря на это многоцикловая усталость вызывает необратимые изменения на мезо- и микроуровнях. Основной характер усталостного нагружения можно проследить по кривой усталости или кривой Вёлера (Рис. 1), которая показывает связь между амплитудными значениями напряжений/деформаций и числом циклов до макроскопического разрушения. На рисунке приняты следующие обозначения: σr — предел выносливости (максимальная амплитуда напряжений, при которой материал образца сохраняет сплошность после неограниченного числа циклов), N1 — база циклов нагружения (число циклов, после которого образец остается целым), (ar)N — предел выносливости (амплитуда напряжений, при которой образец разрушается на заданной базе Np).

Одна из первых эмпиричесих моделей поврежденности для описания многоцикловой усталости предложена А. Пальмгреном и А. Майнером [22, 23] и представляет правило линейного суммирования повреждений.

Уравнения модели справедливы только для одноосного напряженно-деформированного состояния, что является ограничением модели. Данный подход получил развитие в работах Л.М. Качанова [24, 25] , Ю.Н. Работного [26, 27] и других авторов [28] . В этих работах предполагается, что процесс накопления повреждений зависит от совокупности переменных вида действующих напряжений, числа циклов нагружения и накопленной поврежденности. Дальнейшее усовершенствование моделей этого типа заключается в модификации характерных нелинейных зависимостей между скоростью накопления повреждений и указанными переменными. Более подробное описание особенностей моделей накопления повреждений и разрушения приведено в [29] .

По получению кривой Вёлера модели материалов условно можно разделить на две группы: эмпирические и структурные. Первая группа базируется на аппроксимации экспериментальных данных с возможной косвенной интерпретацией механизмов накопления повреждений. Вторая группа опирается на связь усталостной прочности с механизмами накопления повреждений и структурой материала (размером неоднородностей, разбросом физико-механических свойств и другим).

Следующий этап формирования представлений о накоплении повреждений в материале связан с введением деформационного вклада, а процесс разрушения расценивается как критическое событие при достижении характерной деформации. В таком подходе учет напряжений заменяется деформационным вкладом. Модели, основанные на деформационном подходе, предложены в работах С. Мэнсона и Л. Коффина [30] , В.В. Матвеева [31, 32] , В.Т. Трошенко [22] и других. Преимуществом деформационных моделей накопления повреждений является возможность описания переходных режимов нагружения между мало- и многоцикловым режимами усталости. Следует отметить, что для многоцикловой усталости деформационные и силовые подходы становятся эквивалентными.

Применение деформационных моделей привело к гипотезе, что накопление повреждений может обусловливаться накоплением внутренней энергии [33, 34] . Также предложено в качестве параметра модели использовать неупругую энергию петли гистерезиса на каждом цикле нагружения [34] . Такие модели более точно воспроизводят кривую усталости с учетом всех компонент тензоров напряжений и деформаций.

Модели второй группы — структурные, рассматривают повреждение и процесс разрушения материала на различных масштабных уровнях, от атомного до макроскопического. Условно такие модели берут на вооружение вероятностные или физические подходы. Вероятностная модель представления повреждений предложена В. Вейбулом [35] и развивается в работах Я.И. Френкеля, Т.А. Конторовой, В.В. Болотина [36] , С.В. Серенсена [37] , В.П. Когаева [38] , Н.Н. Афанасьева [39] , С.Д. Волкова [40] . Вероятностно-статистические модели применяются при описании одноосных циклических нагружений и основываются на гипотезе наислабейшего звена. Источником разрушения полагается самый опасный дефект. Вероятностный подход имеет трудности при представлении многоосного циклического нагружения и учете напряженно-деформированного состояния.

Физические подходы к определению процессов накопления повреждений базируются на законах физики твердого тела. Выделяют кинетические модели повреждения и подходы на основе континуальной теории дефектов. Соотношения кинетической теории прочности впервые используются С.Н. Журковым для оценки временной зависимости предельного напряжения. Применение кинетической теории прочности для представления разрушения при многоцикловой усталости содержится в работах В.Р. Регеля и А.И. Слуцкера [41] . У И.А. Одинга [42] , В.С. Ивановой [43] и В.В. Федорова [44] структурно-физические подходы базируются на подобии с теорией плавления. В таких подходах диссипированная (тепловая) энергия за счет накопления повреждений и дефектов определяется из энергетического критерия повреждения. Учет структурных дефектов в твердых телах, включая металлы и сплавы, на различных масштабных уровнях заложен А. Коттреллом [45] , а дальнейшее формирование теории влияния дефектов прослеживается в работах Т. Екобори [46] , В.И. Владимирова [47] и В.Е. Панина [48 –50] .

Значительный вклад в развитие механики деформирования и разрушения композиционных материалов внесен учеными российской школы механиков под руководством Б.Е. Победри (МГУ, г. Москва) [51] , школы под руководством В.Е. Панина (ИФПМ, г. Томск) в лаборатории механики полимерных композиционных материалов (зав. лабораторией С.В. Панин) [52, 53] и исследователями пермской школы механики композиционных материалов, создателем и руководителем которой являлся Ю.В. Соколкин (ПНИПУ, г. Пермь) [54] , в сотрудничестве с лабораторией механики перспективных конструкционных и функциональных материалов под руководством Е.В. Ломакина [55 –57] , а также ведущими российскими организациями авиационного моторостроения (ЦИАМ им. П.И. Баранова, ФГУП ВНИАМ и АО «ОДК») [29] . Среди зарубежных исследователей следует отметить группу Composite Materials Group, возглавляемую С.В. Ломовым (KU Leuven, Университет г. Левена, Бельгия), занимающуюся моделированием поведения слоистых и тканных композитов и развивающую прямой численный подход на основе метода конечных элементов, в том числе к многоуровневому рассмотрению (на макро-, мезо-и микромасштабах) поврежденности с последующим анализом данных акустической эмиссии и структурных исследований испытанных образцов из композиционных материалов [58, 59] .

Широкое применение получили модели изотропного накопления повреждений [60, 61] , когда эффективные свойства материала определяются через скалярный параметр сплошности 0 <  ф < 1 . В начальный момент ф = 1 и с течением времени ф убывает. Сплошность ф связывается с поврежденностью D соотношением: ф = 1 — D. Предполагается, что изменение поврежденности зависит от действующих напряжений и текущего значения D . В простейшем случае скорость накопления повреждений обуславливается степенью поврежденности, а полученное напряжение ^ ef f = ст /(1 — D) играет роль среднего напряжения на неповрежденной площади при одноосном растяжении. При этом легко показать, что эффективный упругий модуль есть функция поврежденности: E = E 0 (1 — D ) , где Е° — исходный модуль Юнга. В трехмерном случае вводится тензорный параметр D , который характеризует накопление повреждений вдоль главных осей нагружения. Теперь тензор упругих свойств исходно изотропного материала становится зависящим от введенного тензора поврежденности:

E = A I i + ^ (hi+!_ш )+ C i ( I i • D + DJ i )+ C 2 (hi • D + DJ ii + I_m • D + D ^ 1_Ш ) , (1)

где λ , µ — параметры Ламе, C _i — параметры модели, которые в общем случае могут представляться как функции температуры T и инвариантов тензора поврежденности D [60] , I _I , I _II , I _III — набор независимых изотропных тензоров четвертого ранга, задающих разложение любого изотропного тензора четвертого ранга T = a I I + в I II + Y I III , где a, в, Y — скалярные коэффициенты. Перечисленные параметры, в том числе как 4

функции температуры и инвариантов, необходимо определять по достаточно сложным экспериментальным программам, что вызывает некоторые трудности применения подхода. Преимуществом соотношения (1) является возможность учета наведенной анизотропии за счет тензора повреждений D , и модель может описывать, например, поведение квазихрупких материалов.

В [62] подход обобщен на рассмотрение деградации модуля упругости E при циклическом нагружении с фиксированной амплитудой напряжений. На основе предложенного уравнения кинетики накопления повреждений в композиционном материале (углепластике) разработана математическая модель развития поврежденности, которая позволила качественно и количественно представить деградацию эффективных упругих модулей (Рис. 2а). Проведена идентификация констант модели и получено хорошее соответствие результатов численного моделирования экспериментальным данным в диапазоне многоцикловой усталости (Рис. 2б).

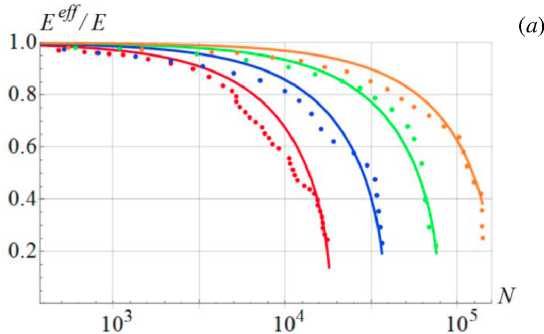
Рис. 2. Результаты численного моделирования деградации упругого модуля для случая циклического нагружения при разных значениях амплитуды напряжений ( а ) и соответствующая критическим точкам кривая Вёлера ( б ) [62]

Для произвольного анизотропного материала учет накопления повреждений требует введения тензоров поврежденности более высокого ранга, например четвертого [63] . Практическое применение такого подхода показано в работе [64] . Кратко изложим основные положения модели. Она опирается на представление закона упругости через тензор упругих свойств E или тензор податливости C , которые задают линейную связь тензоров напряжений σ и деформаций ε

О = E : £ = £ : E , _e = C : о = о : C . (2)

Неупругая составляющая деформаций за счет повреждения материала учитывается как деградация упругих свойств:

o = E : (£-£d) ,

£ d = K i m , (в частности, m = dQ / d o ) ,

∂F

F = о :

∂ σ

- Hk ,

κ

H =

∂F ∂κ

σ

где тензор m задает направление роста повреждений и в частном случае может определяться градиентом потенциала Q в пространстве напряжений для поля неупругой деформации £ d , ik — неупругий, по аналогии с теорией упругопластичности, множитель, F характеризует предельную поверхность неупругого нагружения, H является параметром упрочнения/размягчения среды. Для активной деформации задаются условия: F = 0 , F = 0 , K i > 0 , при разгрузке F <  0 и /К = 0 , то есть отключается неупругая деформация £ d = 0 и осуществляется чисто упругая разгрузка материала. Такой прием приводит к математическим представлениям, эквивалентным представлениям упругопластичности, но вызывает некоторые вычислительные трудности.

Соотношения (3) - (5) с учетом взаимной обратимости тензоров упругих свойств и податливости E : C = C : E = ( I II + I III )/2 = I 4 , то есть того, что их произведение равно единичному тензору в пространстве тензоров четвертого ранга, позволяют перейти к зависимости скорости накопления неупругих деформаций от скорости деградации упругих свойств через податливость и текущие напряжения следующего вида:

£ d = C : о .

В результате уравнения можно переформулировать для тензора податливости как деградацию упругих характеристик:

C = к M , m = M : о ,                                  (7)

где /К определяет величину тензора податливости C , а тензор четвертого ранга M — направление его роста.

Оставаясь в рамках классической теории упругости, наложим на тензоры условие симметричности по соответствующим парам индексов, исходя из симметрии тензоров напряжений и деформаций. Уравнение (7) описывает кинетику изменения 21 компоненты тензора C в соответствии с замыкающими уравнениями (3)-(6), что приводит к необходимости дополнительного задания 21 компоненты тензора M. Альтернативным вариантом является введение сокращенного набора переменных, которые также будут характеризовать процесс накопления повреждений и определяться переменными Γ∗ (как скаляр, вектор или тензор более высокого ранга), где нижний индекс звездочка обозначает отвечающий рангу набор индексов. Тогда упругие характеристики становятся зависимыми от исходных свойств и введенных переменных поврежденности Γ∗ :

с=С(С0Л), C=—оГ., ∂Γ∗ где C0 — исходная упругая податливость неповрежденного материала, C = C (С0 ,Г*) — известные непрерывно дифференцируемые функции, а знак «о» определяет полную свертку по индексам-звездочкам *. По аналогии с уравнениями (4) и (7) для переменных поврежденности запишем эволюционные уравнения деградации упругих свойств:

Г ^    к^ В ^ ,

M =£ ов . . ∂Γ _∗

Рассмотрим пример деградации упругих свойств для изотропного накопления повреждений, задаваемой скалярным параметром 1 — D. Тогда тензоры упругих свойств и податливости представятся в виде: E = (1 — D ) E 0 , C = (1 — D ) C ⁰ , где E 0 и C 0 — соответственно, исходные тензоры упругости и податливости, а уравнение

(8) можно выразить следующим образом:

C =

D C 0 .

(1 — D ) 2

Уравнение (10) задает кинетику изменения обратных секущих модулей (упругих податливостей) в зависимости от параметра поврежденности D как аналога параметра Γ ∗ в кинетических уравнениях (9) . В процитированной выше работе [63] предложено учитывать анизотропное накопление повреждений с помощью полусимметричного тензора четвертого ранга α и произведены все необходимые выкладки. Приведем лишь конечные соотношения. В силу симметрии свойств, а также учитывая (2) , тензоры упругости и податливости представим в виде:

E = а ^-1 : E 0 : а ^-1 ,   C = а : C 0 : а .

При изотропном накоплении повреждений тензор а = ф - 1 1 4 является изотропным тензором четвертого ранга с одним независимым параметром ф =ф1— D, определяющим сплошность среды, а уравнение кинетики при записи через ϕ становится эквивалентным уравнению (10) . Если накопление повреждений анизотропно, необходимо ввести тензор сплошности, выраженный через тензор поврежденности второго ранга: у = I — D (здесь I — единичный тензор второго ранга), с дополнительно введенным тензором w , собственные числа которых связаны соотношениями ^ (k) = w ² _k ) = 1 — D (k) . Тогда собственные значения D (k) будут характеризовать накопленную поврежденность вдоль характерных направлений, а тензор поврежденности четвертого ранга можно представить как а = w ^-1 • I 4 • w ^-1 . Для частного случая ортотропного материала, опуская громоздкие выкладки, приведем лишь матрицу упругих податливостей, связывающую вектор деформаций { £ 11 ,£ ₂₂ ,£ ₃₃ ,Y 12 ,Y 2₃ ,Y 31 } T и вектор напряжений { оп,ст ₂₂ ,ст ₃₃ ,т ₁₂ ,т ₂₃ ,т ₃₁ } ^т , записанную через технические упругие константы с учетом поврежденности (индекс T означает операцию транспонирования):

1 /( ф ? Е 1 )     — v ₁₂ /( ф ₁ ф ₂ E ₂ )

^{— v} 1з ^{/( ф} 1 ^ф з ^E з ^{) —} ^ 23 ^{/( ф} 2 ^ф 3 ^Е 3 ) 1 /( Ф 3 Е з )

¹ / ^(ф 1 ^ф 2 ^G 12 ⁾

¹ / ^(ф 2 ^ф 3 ^G 23 ⁾

^1/(ф 3 ^ф 1 ^G 1з )

— v ₂₁ /( ф ₂ ф ₁ E ₁ )     1 /( ф 2 Е ₂ )

, orth_ ^{— v} 31 ^/(ф 3 ^ф 1 ^E 1 ^{)   — v} 3₂ / ^(ф 3 ^ф ₂ ^E ₂ ⁾

ij

Здесь: E 1 , E 2 , E 3 — модули Юнга; G 12 , G 23 , G 31 — модули сдвига; ν 12 , ν 13 , ν 23 , ν 21 , ν 31 , ν 32 — коэффициенты Пуассона, на которые накладываются ограничения согласно условию симметричности матрицы упругих свойств:

^V 21 / E 1 = ^V 12 ^{/ E} 2 , ^V 31 / E 1 = ^V 13 ^{/ E} 3 , ^V 32 ^{/ E} 2 = ^V 23 ^{/ E} 3 .

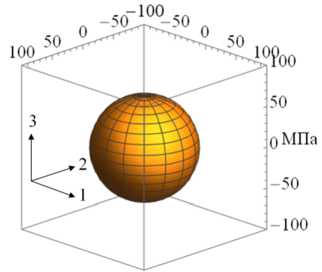
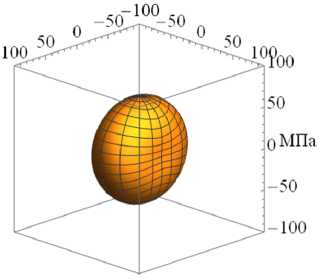
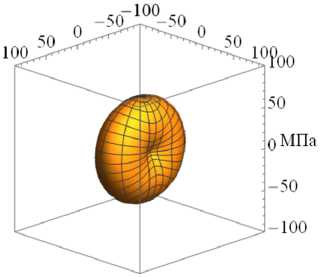
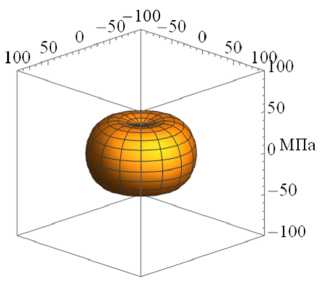
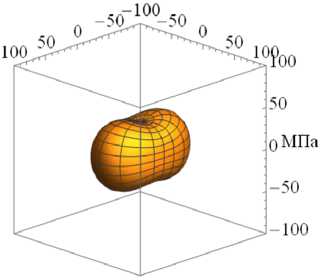
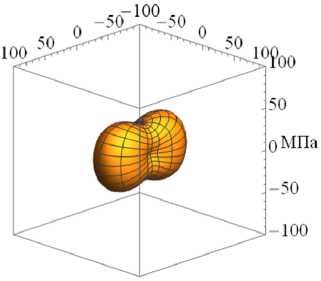
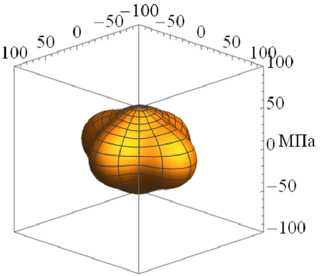
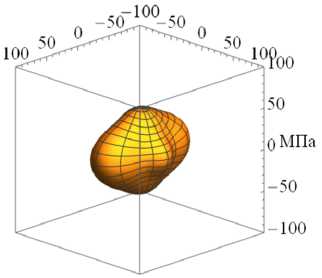
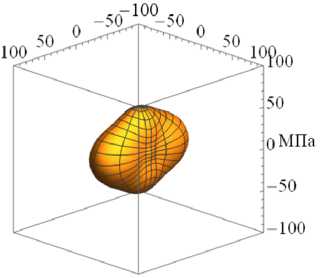
На рисунке 3 приведены характерные поверхности распределения модуля упругости E в зависимости от различного вклада накопленных повреждений вдоль одной из осей, а именно к = 1 (направление осей см. на Рис. 3а ) при разных значениях ϕ 1 для различных видов исходной симметрии начальной матрицы упругих податливостей (11) : изотропной (Рис. 3а , б , в ), трансверсальной (Рис. 33 г , д , е ) и ортотропной (Рис. 3ж , з , и ).

Исходные свойства (при ф 1 = 1 ) для каждого вида симметрии представлены поверхностями на рисунке 3 а , г , ж . Влияние накопления поврежденности только по одной главной оси сказывается на определенных компонентах матрицы упругих податливостей (11) , то есть эффективный модуль Юнга деградирует вдоль одного направления (E 1eff = Ф1Е 1 ) и вызывает изменение двух других модулей сдвига и недиагональных элементов, но при этом модули Юнга по другим ортогональным направлениям не меняются.

При независимом изменении поврежденности по двум направлениям, например, по ϕ 1 и ϕ 2 , будут изменяться все компоненты (11) , кроме компоненты 33. Также может бы ть р ассмотрен тривиальный случай деградации одновременно по всем трем направлениям ф = ф1 = ф ₂ = фз = у/ 1 - D, что соответствует изотропному накоплению повреждений (10) .

Исходя из этих представлений в настоящей работе предлагается модификация модели упругого твердого тела с дефектами, заключающаяся в определении тензора податливости C на основе мезоскопического подхода, то есть когда реакция материала на меньшем масштабном уровне (в ячейке периодичности) находится численно, методом конечных элементов. Аналогичные подходы впервые использовались в турбулентности — это так называемые подсеточные модели. Подобные задачи возникают при численном анализе неоднородных сред сложной структуры на малых масштабах и присущи самым разным областям физики, например, в гидродинамике при изучении турбулентных течений и течений в пористых средах, в теплофизике при анализе теплопередачи в многомасштабных неоднородных средах, в молекулярной динамике и электротехнике [65] . При этом значительно снижаются требования к вычислительным ресурсам, поскольку полные уравнения усредняются по мелкомасштабным компонентам. Реализация определения упругих модулей представительного объема

( a )

( в )

( г )

( е )

( ж )

( з )

( и )

Рис. 3. Характерные поверхности распределения модуля упругости при различном вкладе накопленной поврежденности и различной симметрии: изотропной ( а–в ), трансверсальная ( г–е ), ортотропная ( ж–и ); исходное состояние при ϕ 1 = 1 ( а , г , ж ); ϕ 1 = 0.75 ( б ), ( д ), (з); ϕ 1 =0.5 ( в , е , и )

композита, в том числе с учетом накопления повреждений, будет рассмотрена далее, в четвертом разделе.

Ранее, в [66] , уже предложена макроскопическая модель ортотропного композиционного материала, описывающая накопление повреждений. Теоретические исследования с ее использованием были направлены на изучение слоистого стеклопластика. Разработанные подходы численного моделирования адаптированы к квазистатическому деформированию (в неявный решатель для пользовательской функции UMAT с моделью разрушения XFEM встроена функция UDMGINI, которая определяет критерий разрушения) и к динамическому деформированию (применяется пользовательская функция VUMAT со встроенным алгоритмом удаления разрушенных элементов). Проведено численное моделирование квазистатического и динамического деформирования, а также разрушения ортотропного композиционного материала при различных условиях нагружения. Сравнение результатов численного моделирования с экспериментальными данными показало их хорошее соответствие и позволило получить картины разрушения, выявило характерные зоны образования трещин в композиционном материале, наблюдаемые также в натурных испытаниях [66] .

Разработанная структурно-феноменологическая модель представительного объема ортотропного композиционного материала с учетом накопления повреждений нуждается в верификации. В данной работе модель верифицируется по данным квазистатических испытаний в части описания деградации упругих свойств. Для этого проводились эксперименты, в которых измерялась скорость звука в углепластике.

• 3.    Экспериментальные исследования накопления повреждений в композиционных материалах

• 4.    Численное моделирование накопления повреждений в ортотропном композиционном материале

Далее, прочность и ресурс композиционных материалов оцениваются по результатам экспериментальных и теоретических исследований поведения композитных образцов, проведенных на экспериментальном комплексе в лаборатории физических основ прочности ИМСС УрО РАН, включающем разрывные машины (электромеханическую Shimadzu AG-X Plus, электромеханическую Testometric, сервогидравлическую BIS-100), систему акустической эмиссии (АЭ) Vallen AMSY-6 и систему StrainMaster неинвазивного измерения формы, деформаций и напряжений в твердых, жидких и гранулированных средах. Этот комплекс оборудования позволяет проводить механические испытания стандартных композитных образцов при разных видах нагружения (при растяжении, изгибе, сдвиге) с одновременной регистрацией данных акустической эмиссии и полей распределения перемещений (полей деформации) на поверхности образца [67] .

Ранее авторами получены результаты экспериментального исследования закономерностей накопления повреждений в образцах из стекловолоконного тканого ламината, изготовленного методом вакуумной инфузии, при квазистатическом одноосном растяжении с непрерывной регистрацией акустической эмиссии (АЭ). Проведенный корреляционный и мультифрактальный анализ данных АЭ дал возможность получить новые сведения о статистических свойствах накопления повреждений при деформировании и интерпретировать полученные закономерности в терминах скорости диссипации энергии и количества задействованных механизмов разрушения (каналов диссипации). Использование метода ядерной оценки плотности источников АЭ при решении задачи линейной локации позволило выявить сложную пространственно-временную многомасштабную организацию процесса накопления повреждений, включающую в себя стадии его дискретной по времени активизации и миграцию по образцу в виде локализованных в пространстве и времени зон [68, 69] .

Установлено, что деформирование образца состоит из двух стадий, каждая из которых характеризуется своими статистическими свойствами параметров АЭ. Так, первой стадии отвечает фликкер-шумовая динамика максимальных амплитуд импульсов АЭ с широким мультифрактальным спектром и коррелированным во времени их появлением. На второй стадии происходит переход от фликкер-шумовой и мультифрактальной динамики к коррелированной во времени монофрактальной динамике максимальных амплитуд импульсов АЭ с их появлением, некоррелированным во времени. Такое изменение статистических свойств процесса накопления повреждений может трактоваться как увеличение скорости диссипации энергии с одновременным уменьшением возможных каналов диссипации (доступных механизмов микроповреждений) при приближении к моменту разрушения и резкому падению упругих характеристик, обусловленным интенсификацией накопления повреждений.

Целью экспериментальных исследований в данной работе было измерение скорости звука в образце из слоистого углепластика для определения деградации эффективных упругих модулей, обусловленной накоплением повреждений, и последующей верификации разработанной структурно-феноменологической модели деформационного поведения и разрушения композита. Эксперимент проводился на универсальной нагружающей машине BISS-00-100 на образце из углепластика в виде полосы шириной 25 мм, толщиной 2 мм и длиной 250 мм. На образце закреплялись датчики, регистрирующие АЭ и выступающие в роли излучателей и микрофонов. Деформация образца находилась с помощью системы корреляции цифровых изображений StrainMaster (фирмы La Vision). Ход эксперимента заключался в ступенчатом нагружении образца постоянной нагрузкой от 5 до 50 кН и фиксировании на каждом этапе значений деформации и скорости звука. Шаг нагружения был неравномерным: в начале эксперимента он равнялся 5 кН, на заключительных этапах уменьшался до 1 кН для получения более точных данных в критической области. По результатам эксперимента установлено монотонное падение скорости звука с увеличением нагрузки. При критической нагрузке — перед разрушением, скорость звука уменьшалась более чем в два раза по сравнению с исходной. Сравнение данных эксперимента и численного моделирования производится ниже.

В данном разделе представлены результаты численного (МКЭ) моделирования ячейки периодичности композиционного материала с целью определения эффективных упругих модулей, диаграмм деформирования и характеристик прочности при растяжении и сдвиге в плоскости образца.

Рассмотрено два подхода к расчету эффективных свойств с использованием МКЭ. В первом подходе моделировались свойства ячейки периодичности однонаправленного композиционного материала, а затем свойства усреднялись по слоям укладки, например 0/90 град. Во втором подходе решалась прямая задача моделирования свойств ячейки периодичности для двух слоев с укладкой 0/90 град. В обоих случаях объемная доля волокон составляла 0.65. Для армирующего элемента (углеродное волокно) упругие модули задавались равными E = 200 ГПа и v = 0.25, для связующего (эпоксидная смола) — E = 3 ГПа и v = 0.35. В прикладном пакете конечно-элементного анализа COMSOL Multiphysics 6.0 численно моделировалась ячейка периодичности композиционного материала с однонаправленной укладкой волокон и укладкой 0/90 град. Матрица упругости находилась из решения задачи статики (использовался модуль Solid Mechanics/Linear Elastic Material) при всех различных нагружениях: на одноосное растяжение по трем осям, на сдвиг в трех направлениях. Рассматривалась аффинная деформация ячейки периодичности. При одноосной деформации для ячейки периодичности по соответствующим двум граням имели место однородные перемещения вдоль нормали, по остальным граням — условия проскальзывания. Для сдвига на двух противоположных гранях задавались перемещения в двух плоскостях с противоположными знаками, по остальным граням — периодические граничные условия (равенство перемещений по противоположным граням). Эффективные модули вычислялись как средние по соответствующим граням напряжения, отнесенные к полным деформациям (продольной при одноосном растяжении, сдвиговой для сдвига), вычисляемым явно по известным на гранях перемещениям и геометрическим размерам ячейки периодичности.

Установленные в результате численного моделирования значения упругих констант (в плоскости образца) приведены в таблице. Модули Юнга соответствуют экспериментальным значениям при растяжении образцов (ГОСТ 25.601-80). Значения модуля сдвига также получены путем испытаний (по ГОСТ 32658-2014) образцов на растяжение под углом ±45 град, что соответствует моделированию одноосного растяжения ячейки с укладкой волокон ±45 град. Дополнительно использовалась формула, по которой вычислялся модуль сдвига G в плоскости (при испытаниях по ГОСТ 32658-2014) согласно модели осреднения по слоям (по методу Фойгта): G = EEX/[2(2E — Ех (1 - v))], где E — модуль Юнга на растяжение, Ех — модуль Юнга для образца ±45 град, ν — коэффициент Пуассона. Из таблицы видно, что эти значения хорошо согласуются с данными численного моделирования и эксперимента.

Таблица: Значения упругих модулей в плоскости образца

Модуль	E xx , E yy ,ГПа	G xy ,ГПа	ν
МКЭ	62.7	24.2	0.16
МКЭ+осреднение по слоям	65.0	23.8	0.17
Эксперимент	63±2	24±1	-

Для учета влияния повреждений на упругие характеристики композита в МКЭ-расчет был добавлен программный модуль General Form PDE, который позволяет численно решать уравнения для дополнительных переменных, отвечающих за накопление повреждений и удовлетворяющих гипотезе аддитивности упругих и неупругих деформаций, обусловленных повреждениями (при этом повреждения характеризуются тензорным параметром порядка p). Данная гипотеза приемлема, так как обусловленная дефектами деформация намного меньше упругой деформации. Реакция на нагрузку каждой компоненты упругого композита с повреждениями выражалась нелинейной, имеющей вид полинома тензорной функцией p:

f (k) ⁽ P )

⁽² P c ^- Р )

= ^ c ----2--- p .

P 2

Ее характерный вид представлен на рисунке 4а (см. сплошную линию). При этом σ c есть предел прочности компонента композита.

Тогда для тензоров деформаций, напряжений и поврежденности можно записать следующие выражения:

V^G = 0, e = (Vu+VuT)/2,

E = C (k) : G + p ,

G = f (k)(p), где e — тензор деформации, u — вектор перемещений, g — тензор напряжений, C(k) — тензор упругих податливостей каждой компоненты композита (этот тензор является обратным тензору упругих свойств), p — тензор поврежденности, обусловленный образованием дефектов вследствие деформации, f (k) (p) — нелинейная реакция материала. Математическую постановку задачи следует дополнить граничными условиями для случаев растяжения или сдвига.

На рисунке 4а для проверки адекватности расчета нелинейной реакции материала маркерами показаны зависимости напряжений от параметра p в продольных и поперечных волокнах. На рисунке 4б представлены характерные расчетные кривые при одноосном растяжении ячейки периодичности с укладкой волокон 0/90 град. Предел прочности продольных волокон соответствует максимуму на зависимости напряжений от параметра порядка p и дает хорошее согласование с прочностью всего образца, полученной в эксперименте. На диаграмме растяжения представительного объема (кривая 1 , Рис. 4б ) наблюдается изгиб, что связывается с деградацией эффективного модуля упругости.

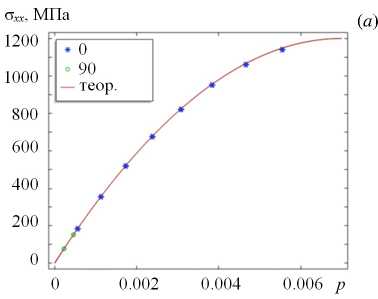
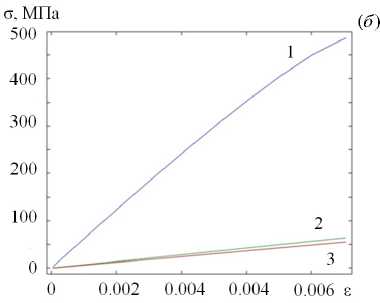
Рис. 4. Зависимость напряжения от накопленных повреждений в волокнах с укладкой 0/90 град ( а ) и кривые деформации ( б ), соответствующие одноосному квазистатическому растяжению образца с укладкой 0/90 град; компоненты напряжений: 1 – σ xx , 2 – σ yy , 3 – σ zz

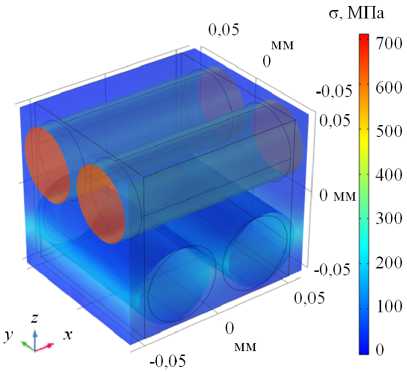
Характерные распределения интенсивности напряжений и деформаций, обусловленных дефектами, при растяжении вдоль и поперек образца, а также при сдвиге представлены на рисунках 5 –7. При деформации вдоль образца (Рис. 5) напряжения возрастают в основном внутри волокон, ориентированных вдоль оси нагружения. При этом существенное накопление повреждений происходит в волокнах, ориентированных вдоль оси нагружения (0 град). Незначительные повреждения наблюдаются также и в волокнах, расположенных к оси растяжения под углом 90 град.

При поперечном растяжении ячейки (Рис. 6) наблюдается концентрация напряжений в матрице, что в свою очередь может связываться в большей степени только с разрушением матрицы, а прочность в этом случае соответствует данным экспериментов на межслоевое разрушение, то есть повреждения накапливаются на границе матрица–волокно.

Результаты моделирования при сдвиге в плоскости образца приведены на рисунке 7. Распределение напряжений носит подобный характер в слоях +45 град и –45 град, так как они одинаково ориентированы по отношению к оси растяжения. Незначительное накопление повреждений при сдвиге наблюдается также на границе волокно– матрица. Таким образом, вычисляемая по предложенной методике матрица упругих свойств, критические значения характеристик прочности углеродных волокон и матрицы полностью определяют деформационное поведение и разрушение углепластиков при растяжении и сдвиге.

Разработанная структурно-феноменологическая модель верифицирована с помощью эксперимента по определению данных акустических свойств углепластиков и позволяет описывать влияние накопления

( a )

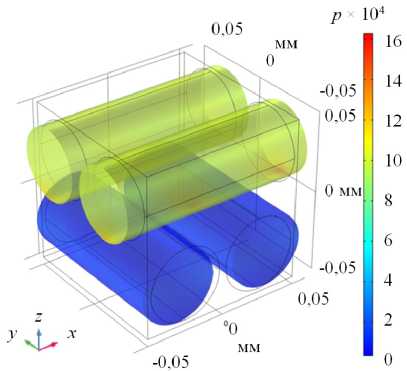
Рис. 5. Характерные распределения продольных напряжений ( а ) и накопленной поврежденности ( б ), соответствующих одноосному квазистатическому растяжению образца с укладкой 0/90 град

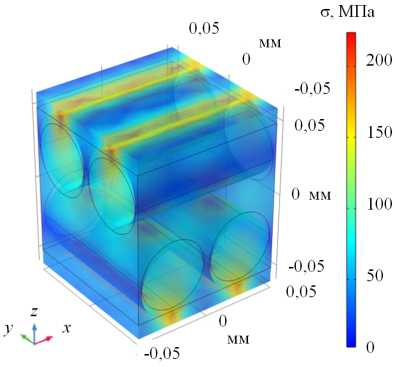
( a )

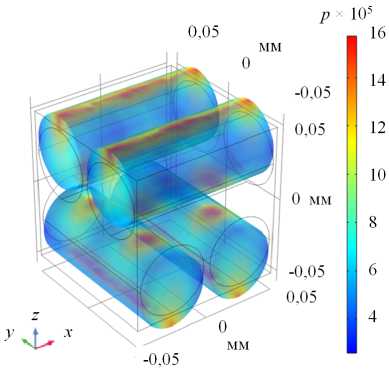
Рис. 6. Характерные распределения поперечных напряжений ( а ) и накопленной поврежденности ( б ), соответствующих поперечному растяжению слоя композита

повреждений на эффективные упругие свойства и характеристики прочности. На рисунке 8 для сравнения приведены результаты деградации упругих свойств, обусловленной накоплением повреждений и, как следствие, падением скорости звука. Модель адекватно отражает падение эффективного модуля упругости образца в соответствии с численным моделированием эффективных упругих свойств для ячейки периодичности композита. Предел прочности вдоль оси растяжения соответствует резкому падению модуля упругости, обусловленному деградацией акустических свойств вследствие накопления повреждений, и согласуется с экспериментальными данными по квазистатическому растяжению образцов.

Одной из основных задач исследования являлась разработка модели представительного объема композиционного материала, состоящего из двух компонент: связующего (эпоксидной смолы) и элементов армирования (углеродных волокон). Реализована методика расчета упругих эффективных свойств представительного объема композита на основе МКЭ. Получены результаты численного моделирования для двух ситуаций. В первой ситуации осреднялись эффективные свойства по слоям из однонаправленного композита, при этом свойства каждого слоя также рассчитывались МКЭ, во второй — использовался прямой метод моделирования структуры по слоям. Оба метода демонстрируют хорошее соответствие друг другу, а также экспериментальным данным.

Следующим этапом был учет накопления поврежденности в композите. Для этого с помощью дополнительного программного модуля General Form PDE в конечно-элементную модель добавлялись уравнения для тензорной переменной, характеризующей неупругую деформацию за счет образования и роста новых дефектов. В процессе а. МПа

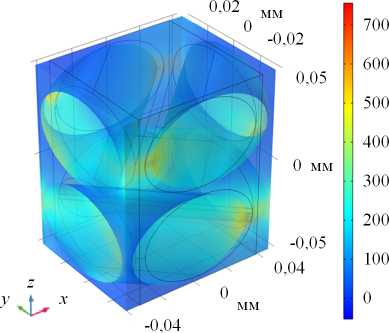
( a )

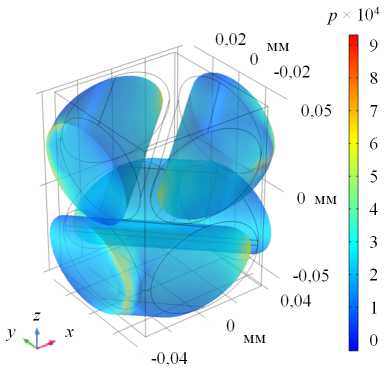
Рис. 7. Характерные распределения поперечных напряжений ( а ) и накопленной поврежденности ( б ), соответствующих одноосному растяжению образца с укладкой +45/–45 град (эксперимент на сдвиг в плоскости)

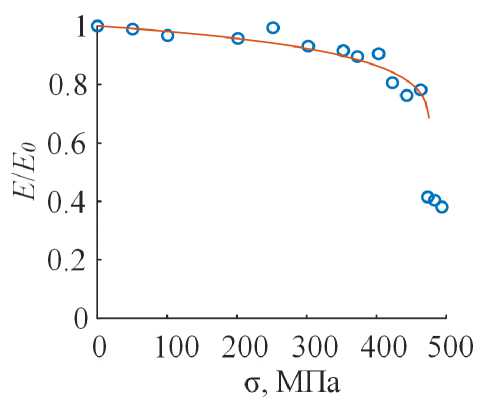
Рис. 8. К верификации модели с учетом деградации упругих свойств: кружками показаны данные акустических измерений скорости звука в композите (представлено нормированное значение продольного модуля Юнга) и расчетная кривая (сплошная линия)

накопления дефектов как в волокнах, так и в матрице, происходит деградация упругих модулей. При этом остаточная поврежденность может быть принята во внимание в представленной во втором разделе формулировке через зависимость эффективных упругих модулей от параметра сплошности (11) . Данный подход позволяет рассматривать накопление повреждений при квазистатических и динамических нагружениях, а также при повторяющихся нагрузках, в том числе со сменой направления нагружения. Следует отметить, что ограничение данного подхода при использовании пакета прикладных программ COMSOL Multiphysics заключается в недостаточности реализации разрушения в рамках конечно-элементной формулировки, в отличие от других пакетов, например ABAQUS, в котором методы моделирования разрушения представлены в большем объеме. Возможность включения в модель макроскопического разрушения показана в предыдущих исследованиях авторов (см. [66] ). Разработанный подход может быть распространен в дальнейшем на моделирование слоистых структур с эффективными упругими свойствами каждого слоя и с учетом накопления повреждений.

• 5.    Заключение

В статье сформулирована и решена задача моделирования эффективных упругих свойств представительного объема ортотропного композиционного материала с учетом накопления повреждений. Проведены экспериментальные исследования по определению влияния накопления повреждений в процессе деформации углепластиков на акустические свойства с целью получения эффективных модулей упругости и верификации развиваемых моделей деформирования и разрушения композитов с повреждениями. Решение задачи нагружения ячейки периодичности композиционного материала численно, на основе МКЭ, позволило вычислить эффективные упругие модули в зависимости от накопленных повреждений, обусловленных зарождением и развитием дефектов при деформировании. Найденные эффективные упругие свойства углепластика хорошо согласуются с экспериментальными данными и таким образом разработанная структурно-феноменологическая модель верифицируется.

Исследование выполнено за счет гранта Российского научного фонда (проект № 21-79-30041),