Модель получения полимерных стабилизаторов композитов с заданным составом макромолекулы

Кинетические закономерности бинарной сополимеризации хорошо изучены и представлены широким спектром информационной справочной литературы [1, 2]. Согласно данной информации мгновенный состав сополимера в условиях радикальной сополимеризации зависит от исходного соотношения, концентрации вступающих в реакцию мономеров и их соотношения, различной реакционной способностью, количественно связанной с константами сополимеризации [3, 4]. Существенная разница в реакционной способности мономеров приводит к образованию неоднородных по молекулярным массам и составе макромолекул сополимеров. Это приводит к низкой вероятности достоверного прогноза о возможностях таких сополимеров в составах различных композиционных материалов, поскольку свойства усредненных, но значимо отличных по составу и структуре сополимеров будут изменяться в широком диапазоне [5, 6]. Поэтому целью настоящей работы являлось получения рабочей технологической формулы, регламентирующая добавку сомономера во времени, которая обеспечивает синтез макромолекулы сополимера с постоянным составом и соответственно с прогнозируемыми свойствами, как сополимера, так и модифицированных им пористых композиционных материалов.

Методы

В основу математического моделирования положена теория кинетики сополимеризации, учитывающая реакционную способность мономеров посредством констант сополимеризации реагирующих сомономеров. Исходной базой служила кинетика сополимеризации двух сомономеров, существенно отличающихся по своей реакционной способности, что требовало последовательную, ступенчатую подачу менее реакционноспособного мономера в реакционную среду с более активным мономером [7].

Результаты и обсуждение

Исходным выражением (1) послужило соотношение концентраций реагирующих мономеров в виде постоянной величины:

М

—1- = const = x .

с_{М 2}

Уравнение (1) можно преобразовать в равенство (2), рассматривая отношение концентраций реагирующих мономеров в составе образующегося сополимера в следующем виде:

с М_хп      rx + 1

—— = x ----.

с М 2 п      ^r 2 ⁺ x

Рассмотренные два выражения образуются как следствия теории сополимеризации [8], учитывающей реакционную способность каждого мономера с помощью констант сополимеризации (r).

Уменьшение концентрации реагирующего мономера в условиях радикального синтеза можно представить в виде дифференциального уравнения с учетом закона действующих масс [9]

dс_{М 2}

"IT " кэфСМ2 ’ где kэф – константа скорости сополимеризации, учитывающая контанты сополимеризации каждого мономера

Далее проводим операцию интегрирования, что позволяет получить уравнение для изменяющейся во времени концентрации мономера М2 в реакционной смеси согласно экспоненциальному закону [10]:

С м 2 = С М 2^- , (3)

используя конечные условия интегрирования c ^₂ = с _UJ t = 0, где c0₂ - концентрация второго сомономера в начальный момент времени.

Для получения зависимости между концентрациями реагирующих мономеров в условиях радикальной сополимеризации воспользуемся ранее рассмотренными уравнениями и получим необходимое выражение в следующем виде, которое учитывает соотношение сомономеров с о / kэфt

^СМ 1 хс М ₂ ^ХСМ ₂^ .

Воспользуемся условиями материального баланса, чтобы выразить концентрацию второго, менее реакционноспособного мономера М2 ( с ) в полимере которую можно представить в виде следующего равенства

^С М ₂ п    ^С М ₂    ^С М ₂ .

Из уравнения (4) можно заключить, что уменьшение содержания второго мономера М 2 в реакционной массе означает увеличение его в составе сополимера.

Воспользуемся выражением (3), согласно которому можно записать

С м 2 п = С М 2 (1 -^ k * )          (5)

Очевидно также, что См₂ + С м₂п = сМ₂ .

Это следует из характера физического явления и определяется графическими зависимостями, представленными на рисунке 1, аналитической основой для которых являются выражения (3) и (5).

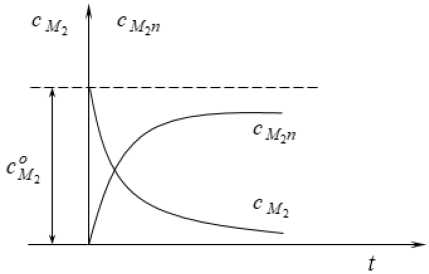
Рисунок 1. Кинетические кривые процесса сополимеризации

Figure 1. Kinetic curves of the copolymerization process

Д^ = ХС^о 0 ^Эф^

^А с м 1   хс м 2     ⁺

+ хс м, r ^ x + i ( 1 "Г^м ) - хс м, '

² r ₂ + х

Последнее выражение несколько изменим, приводя к более лаконичному виду путем работы с одноименными членами ( хс^о ) и квадратными скобками:

^{А с}м 1   ^хсм ₂

^Л г_гх + 1

V Г 2 + х

- ¹ ( -с-

Установим зависимость между содержанием первого мономера в составе сополимера М 1 ( с ) и исходной концентрацией второго мономера в реакционной массе для чего воспользуемся уравнениями (2) и (5)

с м, = хrx + 1 с М ₂ (1 "^ ^kэфt) .      (6)

¹       r₂ + х

Подобное уравнение можно использовать и для второго менее активного мономера М 2.

Необходимо выразить общее содержание первого мономера М 1 ( ^ с_{м 1} ) в реакционной массе и в составе сополимера, что будет соответствовать выражению (7): которое определится его концентрацией в полимеризующейся системе и сополимере:

^ ^см 1 = ^см 1 ^{+ с}м 1 п ^{.           (7)}

Откуда логично вытекает соотношение (8),

о

М ₁         М ₁     М ₁

которое принципиально выражает условие поддержания постоянства соотношения сомономеров в реакционной массе ( x = const ) путем введения определенного количества первого более активного мономера М 1 в реактор. Данный технологический прием способствует образованию макромолекулы сополимера с более стабильным составом и структурой (структуру по составу) [11].

Далее необходимо выразить функциональную зависимость введения определенной концентрации первого мономера А с_м во времени t.

^А см, = фО) .

На основе выше полученных уравнений можно необходимую функциональную зависимость представить следующим образом

Выражение (9) устанавливает закономерность введения в реакционную массу активного первого мономера М 1 , что обеспечивает образование более стабильного по составу и структуре сополимера [12].

Последнее выражение (9) приведем в более удобную для технологии форму, которая требует определения общей константы скорости радикальной сополимеризации k эф в условиях бинарных систем. При этом необходимо использование либо справочной информации или экспериментальное определение констант сополимеризации для каждого мономера бинарной системы. Целесообразно также определять оптимальные соотношения мономеров, обеспечивающие получение сополимеров с заданными составом и структурой.

Для нахождения k эф подвергнем выражение (3) операции логарифмирования [13], что позволяет получить уравнение (10):

ln см₂ = ln см₂ — к фф t . (10)

Уравнение (10) преобразуем к виду (11), которое удобно обрабатывать методом наименьших квадратов [14] для нахождения требуемых коэффициентов:

y = a 0 - к фф • t . (11)

Для интересующих бинарных реакционных смесей мономеров можно использовать справочную информацию о величинах констант скорости или получать их экспериментальным путем. Для новых бинарных систем всю необходимую исходную информацию можно получить при экспериментальном изучении кинетики сополимеризации. Затем определяем требуемый состав сополимеров ( x ), исходную концентрацию менее активного второго мономера ( с ^о ) необходимое время синтеза ( t ). Далее уравнение (9) позволяет рассчитать изменение концентрации первого более активного мономера ( А с_м ) для получения сополимера с заданным составом и структурой.

Заключение

На базе основных положений теории кинетики бинарной сополимеризации, закона действующих масс и метода наименьших квадратов получена рабочая формула, определяющая зависимость дозировки менее активного сомономера во времени с учетом исходного содержания более активного сомономера, а также их констант сополимеризации.

Таким образом, используя текущее значение времени, экспериментальные или справочные величины констант сополимеризации, заданное соотношение сомономеров и начальное содержание более активного сомономера можно рассчитать последовательность введения менее активного сомономера во времени. При этом предварительно рассчитывается эффективная константа кинетики сополимеризации на основе прологарифмированного промежуточного уравнения с использованием метода наименьших квадратов. По справочным данным была построена и проанализирована математическая модель с использованием основных понятий бинарной кинетики сополимеризации.

Компьютерная обработка полученных уравнений показала достоверность применения их в технологической практике синтеза сополимеров на основе сомономеров с существенной разницей в реакционной способности, для которых данная модель наиболее актуальна.