Модель прогнозирования темпов индекса потребительских цен (инфляции) на примере РФ

Инфляция является одной из ключевых категорий экономической теории. Ее регулирование позволяет решить различные проблемы социально-экономического характера, а своевременное прогнозирование способствует оптимальному управлению хозяйственной деятельностью экономических субъектов. Количественные оценки инфляционных процессов получили широкое распространение среди положений теории стоимости денег во времени. Правильный и достоверный расчет будущих темпов изменения цен на продукцию и услуги различной направленности позволяют проектировщику точно оценить устойчивость своих проектов, определить точки безубыточности и найти оптимальную цену продукции, которая будет способствовать максимизации его прибыли. Помимо этого достоверное прогнозирование уровня инфляции позволяет сократить издержки будущих периодов, которые особенно сильно возрастают при кризисных явлениях в экономических системах. В данной статье рассматриваются основные теоретические положения инфляционных процессов с позиций теоретических положений У. Филлипса и предлагается математическая линейная модель множественной регрессии, при помощи которой можно спрогнозировать темпы изменения индекса цен на будущие периоды. Также рассмотрены теоретические положения о доле безработных относительно исследуемой категории и изложены методологические положения о трендовом моделировании данного процесса. На основании построенных моделей были получены прогнозные значения темпов потребительских цен и уровня безработицы для экономики Российской Федерации за 1999 – 2017 гг., а также проведен анализ того, как данные категории будут вести себя в будущем. В заключении статьи предложены варианты ис- пользования спроектированного математического инструмента, в особенности при оценке инновационно-инвестиционных проектов, а также те направления, при помощи которых возможно его совершенствование и улучшение математического инструментария. Следует отметить, что построенная математическая регрессионная модель при доработке оценочных значений показателей может быть использована для расчета и прогнозирования естественного уровня безработицы, который не зависит от инфляционных процессов и явлений, протекающих в экономической и социальной среде общества.

Инфляция, индекс потребительских цен, уровень безработицы, множественная регрессия, трендовое моделирование.

При моделировании сложных экономических систем или процессов, которые протекают в экономике, одной из ключевых категорий является инфляция. Большее значение измерение данного показателя имеет при оценке инновационных, инвестиционных проектов или объектов недвижимости. Данные положения наиболее подробно исследуются в теории стоимости денег во времени [2].

При оценке точки безубыточности какого-либо проекта проектировщик сталкивается со следующими проблемами [15]:

– выход на оптимальный срок реализации идеи;

– формирование адекватной цены продукции, по которой покупатель или заказчик готов приобрести реализованную идею или готовый материальный объект;

– моделирование альтернативного дохода или затрат.

Расчет темпов инфляции связан более всего с последней проблемой. Он закладывается в норму дисконта, которая необходима при приведении разновременных затрат и результатов к единому моменту (точке приведения). Помимо темпа инфляции, норма дисконта включает в себя МР – минимальную реальную норму прибыли и R – коэффициенты учитывающие степень риска. Общая модель нормы дисконта выглядит следующим образом [15]:

E i = y i + Mp i + R i , (1)

Таким образом, целью данного исследования являлось построение рабочей мате-

матической модели, способной прогнозировать значения движения инфляции для будущих периодов.

В официальной статистике РФ представлена динамика рядов во времени по показателям: индекс потребительских цен, характеризующий уровень инфляции за 1999 – 2014 гг. [12] и уровень безработицы за тот же период. Согласно теории У. Филлипса [11; 15] мы предполагаем, что темп инфляции отрицательно связан с уровнем безработицы, т. е. увеличение доли безработных сокращает скорость роста инфляционных процессов, также мы предполагаем, что исследуемый процесс носит инерционный характер, т. е. чем больше темп инфляции в настоящий момент, тем больше он будет в будущих периодах. Также в данную теорию закладывается положение о том, что существует некоторый «естественный» уровень безработицы, не оказывающий влияния на процессы инфляции. В англоязычной литературе данному определению присвоена аббревиатура NAIRU (Not Accelerating Inflation Rate of Unemployment) [10]. Таким образом, теоретическая математическая модель темпов инфляции примет следующий вид:

y i = a(NAIRU i – u i ) + by i–1 ,      (2)

где:

y i – темпы инфляции i-го периода (индекс потребительских цен);

y i–1 – темпы инфляции периода предшествующему i-му отрезку времени;

u i – уровень безработицы i-го периода;

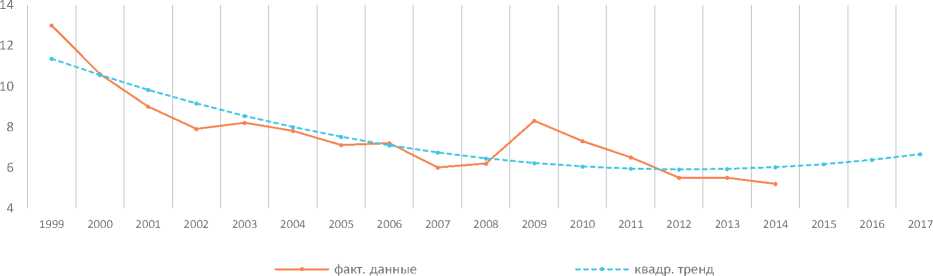
Рис. 1. Динамика уровня безработицы по РФ

Таблица 1. Уровень безработицы в РФ

Год Уровень безработицы Прогнозируемый уровень безработицы 1999 13,0 11,356 2000 10,6 10,558 2001 9,0 9,823 2002 7,9 9,152 2003 8,2 8,543 2004 7,8 7,998 2005 7,1 7,516 2006 7,2 7,096 2007 6,0 6,740 2008 6,2 6,447 2009 8,3 6,218 2010 7,3 6,051 2011 6,5 5,948 2012 5,5 5,907 2013 5,5 5,930 2014 5,2 6,016 2015 – 6,165 2016 – 6,377 2017 6,652 Источник: Регионы России. Социально экономические показатели [Электронный ресурс] : стат. сб. – Режим доступа :

NAIRU i – естественная доля безработных в i-м периоде;

a и b – неизвестные коэффициенты влияния.

Следует отметить, что для прогнозирования темпов инфляции более чем на один период вперед необходима модель прогнозирования уровня безработицы. Данная модель была построена по РФ на основе трендового моделирования (рис. 1), подробно разобранного ранее [1].

Полиноминальная модель квадратичного тренда, согласно скорректированному коэффициенту детерминации (R² скор. ), равному 0,756, наиболее точно описывает сложившу-

юся в экономике России тенденцию в сфере безработицы. При сопоставлении фактических данных с прогнозируемыми можно выделить период 2009 года, который нарушает плавный равномерный спад уровня безработицы РФ. В это время значение исследуемого показателя увеличилось примерно на 34%, что может объясняться влиянием мирового финансового кризиса, протекавшего в экономиках мира на момент 2009 года. Спрогнозированные значения показателя имеют тенденцию к росту (табл. 1).

Следует отметить, что прогнозирование на более длительный срок по данным моделям является проблематичным, т. к. тенден-

ции, протекающие в экономике, описаны при помощи простейших функций, график которых с течением времени будет иметь более пологий характер (кроме линейной модели). Это отразится на прогнозных значениях ускорением темпов роста (или замедления) исследуемой величины.

С учетом функции уровня безработицы модель темпов индекса потребительских цен примет следующий вид:

y i = a(11,36 – 0,83i + 0,03i²) + by i–1 (3)

Для указанных временных рядов (19992014 гг.) оценки параметров уравнения множественной линейной регрессии примут следующий вид:

y i = 51,22 + 0,58y i–1 – 0,7u i (4)

Следует отметить, что статистическое качество полученного уравнения регрессии находится на высоком уровне. При заданном уровне значимости в 5% значения t- статистик находится в пределах заданных норм, что гарантирует адекватность полученных параметров. Коэффициент детерминации равен 0,727. Это указывает на то, что около 72 – 73% поля разброса объясняется полученной статистической моделью. На рисунке 2 представлено графическое изображение регрессии в сопоставлении с фактической информацией.

В иллюстрированном виде уравнение множественной регрессии также довольно хорошо описывает фактические данные по индексу потребительских цен (табл. 2). При сложившихся экономических условиях и их неизменности тенденция данного показателя на перспективу будет носить ниспадающий характер. Согласно уравнению инерционная составляющая инфляции сохраняется на уровне в 60% от предыдущего года (0,58y i–1 ). Рост уровня безработицы на 1% замедляет темпы роста инфляции на 0,7 проц. ед. (0,7u i ).

Прогнозное значение темпов инфляции на 2015 год составит значение на 2% больше, по сравнению с предыдущим годом, но в дальнейшие периоды (2016 – 2017 гг.) будет происходить замедление. Прогнозирование на более длительный период можно осуществлять лишь с учетом получения данных о дальнейших наблюдениях. Это условие применимо как для конечной модели, описывающей изменение инфляции, так и для модели, касающейся уровня безработицы.

Таким образом, спроектированная математическая модель инфляции, в основе которой лежат регрессионные модели простейших математических функций и понятие об автокорреляции, позволяет прогнозировать значения темпов индекса потребительских цен при неизменных экономических условиях на искомые будущие периоды. Полученное уравнение может быть использовано при моделировании бо-

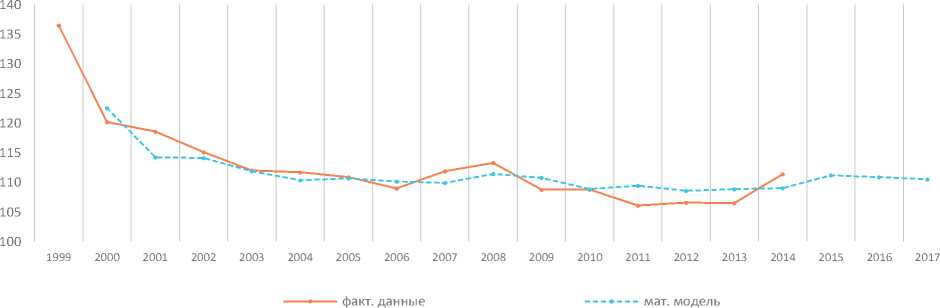
Рис. 2. Динамика темпов индекса потребительских цен РФ

Таблица 2. Темпы индекса потребительских цен (ИПЦ)

Год ИПЦ Прогнозируемый ИПЦ 1999 136,5 – 2000 120,2 122,540 2001 118,6 114,259 2002 115,1 114,108 2003 112,0 111,878 2004 111,7 110,370 2005 110,9 110,689 2006 109,0 110,157 2007 111,9 109,904 2008 113,3 111,437 2009 108,8 110,769 2010 108,8 108,875 2011 106,1 109,437 2012 106,6 108,582 2013 106,5 108,870 2014 111,4 109,024 2015 111,173 2016 110,893 2017 – 110,538 Источник: Регионы России. Социально экономические показатели [Электронный ресурс] : стат. сб. – Режим доступа :