Модель управления температурой при выращивании кремния

Методы вытягивания кристаллов из расплава по способу Чохральского берут начало от работ таких авторов, как R. Nacen, S. Kyrohulos и J. Czochralski. Основа этих методов состоит в том, что небольшую монокристаллическую затравку вводят неглубоко в расплав и затем ее медленно вытягивают из расплава. При вытягивании температуру расплава сначала повышают, что приводит к образованию шейки, затем температуру расплава снижают до первоначального уровня, в результате чего диаметр затравки возрастает. Этот процесс носит название подрезания затравки. Он позволяет получить гарантированную монокристаллическую затравку. После подрезания затравки для перехода в автоматический режим выращивания кристалла по программе, закладываемой в систему управления, производится вытягивание шейки затравки определенного диаметра и длины с одновременным обеспечением заданной скорости вытягивания, что позволяет стабилизировать тепловые условия перед переходом в автоматический режим работы по программе. Выращивание кристаллов кремния производится обычно в протоке инертного газа аргона, при этом расплав помещается во вращающийся тигель (с угловой скоростью вращения в пределах 2–10 об/мин), а затравке с кристаллом придается программируемое вращение (с угловой скоростью в пределах 10–90 об/мин). В процессе вытягивания форма прямого конуса кристалла, его цилиндрической части и обратного конуса, а также процесс последующего медленного отжига кристалла (снижения температуры после отрыва кристалла от расплава) программируется системой управления за счет программного изменения скорости вытягивания кристалла и температуры. Во многих системах управления поддерживается постоянный уровень расплава в тигле и имеются подсистемы измерения и управления текущим диаметром кристалла. Интенсивное перемешивание расплава в тигле за счет центробежных сил позволяет отбросить от кристалла возможные возникающие паразитные кристаллические зародыши и исключить радиальные температурные градиенты, способные вызвать неправильный (боковой) рост кристалла. Это благоприятствует поддер- жанию однородности расплава. При выращивании совершенных кристаллов необходимо избегать тепловых и механических колебаний; при которых нарушается форма кристалла и в нем возникают дефекты. Важно также отметить тот факт, что напряжения, возникающие после вытягивания кристалла из расплава, сводятся к минимуму за счет его последующего медленного охлаждения или так называемого процесса отжига (до 24 ч для кристаллов германия диаметром 270 мм). Процесс вытягивания монокристаллов кремния из расплава по способу Чохраль-ского требует соблюдения целого ряда дополнительных условий, обеспечивающих получение качественного материала заданной геометрии. Кроме чистоты используемого сырья и возможности загрязнения расплава посторонними примесями из тигля и других частей печи, необходимо также создать определенные физические условия, обеспечивающие минимальные дефекты кристаллической решетки в процессе роста кристалла. Изменения скорости вытягивания монокристалла, степени охлаждения и температуры расплава влияют на заданную геометрию выращиваемого кристалла и во многом определяют количество дефектов кристаллической решетки. Особенно сильно влияют колебания температуры расплава (более 0,1 °С) и скорости вытягивания кристаллов [1-3]. Поэтому для выращивания совершенных марок монокристаллов используются автоматизированные системы управления с контролем и управлением текущей площадью кристалла в процессе роста. Микропроцессорная система управления выращиванием монокристаллов кремния представлена на рис. 1. Под управлением системы управления в камере производится выращивание монокристалла диаметром d, со скоростями вытягивания Vзи вращения кристалла W3, при этом расплавленный металл, находящийся в тигле с внутренним диаметром D, вращается с угловой скоростью W Для поддержания постоянного уровня расплава в тигле, кроме скорости подъема тигля вверх V, в системе формируется информация о перемещении тигля Xитц с (дискретностью Ат) и информация Xизц о перемещении кристалла вверх (с дискретностью Аз). Управление от ЭВМ скоростями вытягивания кристалла Vз, вращения кристалла W^ вращения тигля Wt осуществляется через соответствующие приводы. Управление температурой расплава осуществляется на основе формирования задания температуры Т от ЭВМ на регулятор температуры. В качестве датчика обратной связи по температуре используется радиационный пирометр с оптической системой, которая направлена на боковую поверхность графитового нагревателя. Информация о выращиваемом диаметре кристалла поступает с оптической системы на преобразователь, на основе чего в системе формируется текущее положении яркостного ореола мениска кристалла и происходит вычисление сигнала управления, который пропорционален отклонению диаметра выращиваемого кристалла от заданного по программе. Полученный сигнал управления используется для коррекции диаметра выращиваемого кристалла по каналам управления скоростью вытягивания и температурой расплава. Программное задание закона изменения температуры Tв микропроцессорных системах выращивания кремния задается технологом за счет ввода в систе- му управления программы изменения температуры на всех участках выращивания. После выращивания первых образцов заданной марки кристалла, введенный выше программный закон изменения температуры корректируется на основе анализа предыдущих записей. При производстве кристаллов кремния удовлетворительным получается процесс корректировки программного закона изменения температуры после выращивания от четырех до пяти кристаллов заданной марки, что является трудоемким процессом.

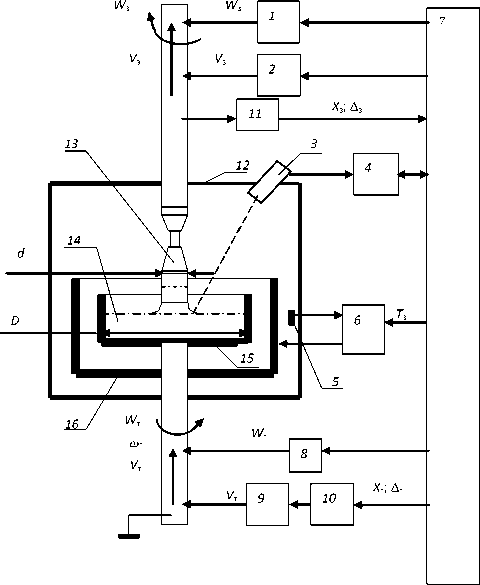
Рис. 1. Система управления выращиванием монокристаллов кремния: 1 - привод вращения затравки; 2 - привод перемещения затравки; 3 - оптическая система;

4 - преобразователь изображения мениска; 5 - датчик температуры; 6 - регулятор температуры; 7 - ЭВМ; 8 - привод вращения тигля; 9 - шаговый двигатель;

10 - блок управления шаговым двигателем; 11 - датчик перемещения затравки; 12 - камера; 13 - слиток;

14 - расплав металла; 15 - тигель; 16 - нагреватель

Приведем математические выражения для формирования программного задания температуры T , которые позволяют автоматизировать данный процесс. Модель управления температурой (рис. 2) при выращивании кремния можно представить в виде выражения

T(x) = F(Z, Y, V (x), L(x), x), где T(x) - средняя температура расплава в зоне фронта кристаллизации; Vзп(x) - программное задание скорости вытягивания кристалла; x - координата перемещения вдоль оси кристалла; L(x) - линейный осевой градиент в твердом кристалле; Z- вектор задания геометрии выращиваемого кристалла; Y- вектор задания теплофизических параметров материала.

Если приравнять вес массы столбика расплава силам поверхностного натяжения, действующим по окружнос- ти, и учесть выражение высоты столбика расплава через уравнение теплового баланса на фронте кристаллизации, то можно получить зависимость диаметра кристалла d от скорости вытягивания Vз и температуры расплава Тв виде следующего выражения [1]:

Выражения по заданию диаметра d _з( x ) и температуры Т ( x ) на прямом конусе кристалла примут вид x ■ [ d , - d _о ] d _з ( x ) = d ₀ + — -------, x i

d = C t

[ L — C v ■ V s ] [ t - T ]

T _3n ( x ) = Т к + C t -^

v—r          E          1 C ' ^TR     ТГ где cv = рж —; Ct = 4-----——; V - скорость вытяги-

^Х тв           Р ж ^-Х _ж ^- g ³

вания кристалла; T к - температура кристаллизации материала; T - средняя температура расплава в зоне фронта кристаллизации; L - линейный осевой градиент в твердом кристалле; E - удельная теплота плавления материала; Х _ж - коэффициент теплопроводности расплава; Х _тв -коэффициент теплопроводности кристалла; g - ускорение свободного падения; с - поверхностное натяжение

[ L о — C v ■ V з_П ( x ) ] x ■ [ d i ^- d о ] d 0 + x ,

где x , - координата завершения формирования прямого конуса кристалла; L ₀- величина осевого градиента в кристалле на конусной части; d ₀ - диаметр вытягиваемой шейки кристалла; d ₁ - диаметр цилиндрической части кри-

сталла.

Выражения по заданию диаметра d _з( x ) кристалла и температуры Т ( x ) на цилиндрической части кристалла

примут вид

расплава; р _ж - удельная плотность жидкого материала; d - диаметр выращиваемого кристалла.

Для задания средней температуры расплава выражение (1) можно представить в виде

T ( % ) = T _K + C t ^[L ^- C^V ■V ⁽ x ^{) ]} ,             (2)

^d з⁽ x )

где d _з( x ) - программное задание выращиваемого диаметра кристалла; V _зп( x ) - программное задание скорости вытягивания кристалла; x - координата перемещения кристалла.

Процесс управления основными параметрами выращивания монокристалла кремния приведен на рис. 3. Используя линейную аппроксимацию параметров на узловых участках выращивания кристалла, можно получить выражения для вычисления программы управления температурой на всех участках выращивания.

d з ( x ) = d i ,

L о ^{+[ x - x} i ^]

T ( x ) = Т к + Ct -----------

⁽ L i ^- L о )

( ^x 2

-

^x i )

d i

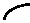
- C v ■ V з_П ( x )

где x ₂ - координата завершения формирования цилиндрической части кристалла; L _i - осевой градиент в кристалле в конце цилиндрической части.

Выражения по заданию диаметра d _з( x ) кристалла и температуры Т ( x ) на обратном конусе примут вид

( x ^- x 2 ) ■ [ d i ^- d о ]

^d з^{( x} ) = ^d i  ---- z _A----- ( ^x з ^{- x} 2 )

Т зп ( x ) = Т к + C t

[ L i - C v ■ V _ln ( x ) ]

Y

d _i

( x - x ₂ ) [ d _i - d _о ] ( ^x з ^{- x} 2 )

Р т

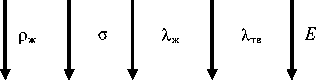
T ( x ) -----►

Рис. 2. Модель управления температурой при выращивании кремния

где x3 – координата завершения формирования обратно- физических постоянных материала кремния [4] приведе- но на рис. 4–6.

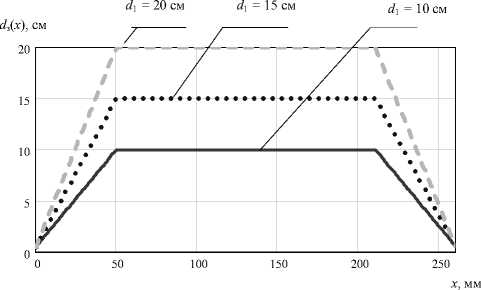
Рис. 4. Задание диаметра кристалла кремния:

го конуса кристалла.

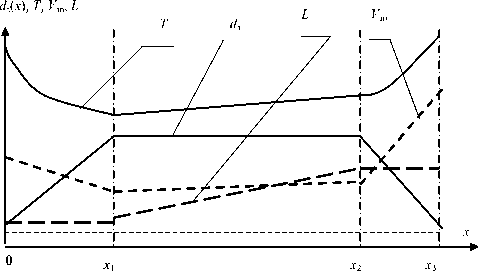
Рис. 3. Здание параметров процесса выращивания кристаллов кремния: d _з – задание диаметра выращиваемого монокристалла; Т – программное задание закона изменения температуры; L – задание осевого градиента; x – перемещение кристалла; x ₁ – координата завершения формирования прямого конуса кристалла; x ₂ – координата завершения формирования цилиндрической части кристалла; x ₃ – координата завершения формирования обратного конуса кристалла; V _зп – программное задание закона изменения скорости вытягивания

Моделирование температуры выращиваемых кристаллов кремния разных диаметров с заданием диаметра и скорости вытягивания на всех участках выращиваемого кристалла на основе приведенных зависимостей и тепло- x1 = 50 мм; x2= 210 мм; x3= 260 мм; d0 = 0,5 см

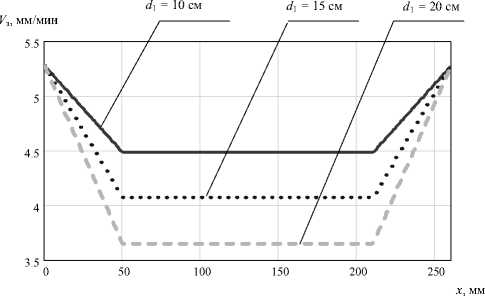
Рис. 5. Задание скорости вытягивания кремния: d ₀ = 0,5 см; x ₁ = 50 мм; x ₂= 210 мм; x ₃= 260 мм

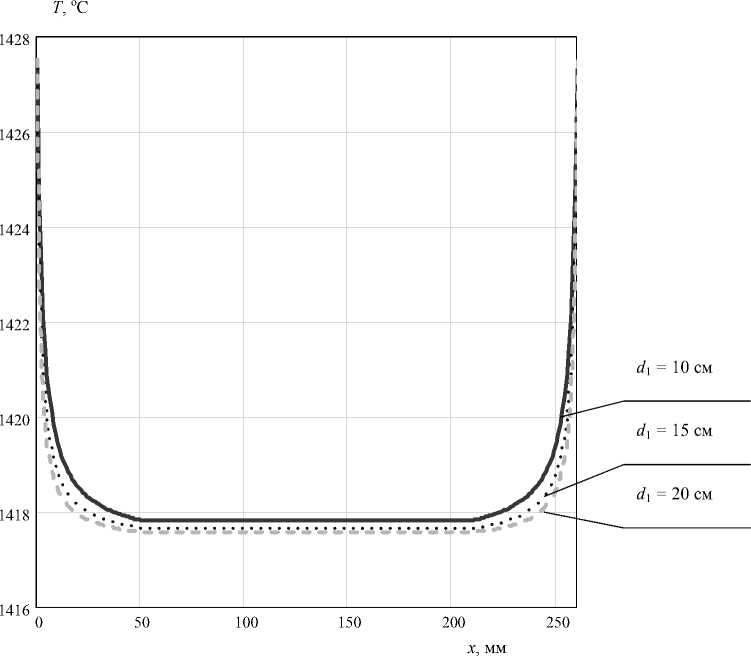
Рис. 6. Задание температуры вытягивания кремния: d ₀ = 0,5 см; x ₁ = 50 мм; x ₂= 210 мм; x ₃= 260 мм

Моделирование программы задания температуры позволяет без процесса предварительного вытягивания монокристалла кремния ввести смоделированное задание температуры в систему управления установкой вытягивания, что значительно сокращает цикл изготовления готовой продукции. Для системы автоматического управления выращиванием кристаллов кремния необходимо учитывать и то обстоятельство, что в системе управления регулирование температуры расплава осуществляется на основе задания и регулирования температуры части боковой поверхности нагревателя с применением оптических пирометров, что можно учесть с помощью измерения и последующего расчета коэффициента связи средней температуры расплава и регулируемой области нагревателя.

Таким образом, предложена математическая модель формирования задания температуры на установке выращивания монокристаллов кремния, которая позволяет при изготовлении готовой продукции смоделировать и автоматизировать процесс ввода программного задания температуры в систему управления установкой перед процессом выращивания монокристалла, что сокращает цикл получения качественной продукции для каждой новой марки выращиваемых кристаллов.