Модель выбора формы лезвия выпуклого шестиугольного диска

В условиях сложившейся экономической ситуации в нашей стране и мире сельское хозяйство становится важнейшей отраслью народного хозяйства. От развития агропромышленного комплекса зависит жизненный уровень и благосостояние населения. Основной задачей производства продукции растениеводства является получение высоких урожаев с хорошим качеством зерна [1]. Повышение эффективности производства продукции растениеводства возможно лишь путем интенсификации, предусматривающей рост урожайности и снижение себестоимости производства возделываемых культур за счет рационального использования удобрений, внедрения высокоурожайных сортов и улучшения агротехники их возделывания [2].

Основную роль в создании условий жизнедеятельности культурных растений играет почва, от ее состояния зависит урожай сельскохозяйственных культур. Для создания оптимальных условий для растений необходима обработка почвы – важное звено в системе агротехнических мероприятий при производстве продуктов растениеводства [3]. Это наиболее энергоемкий элемент практически всех технологий возделывания сельхозкультур: расходуется от 30 до 40% всей энергии, потребляемой в сельском хозяйстве.

В то же время от качественной обработки почвы зависит до 25% формирование урожая. Связана обработка почвы со значительным расходом топливно-смазочных материалов (от 12 до 38% общих затрат на топливо в сельском хозяйстве). Поэтому разработка и внедрение в производство энергосберегающих систем при обработке позволят во многом снизить затраты на производство и обеспечить значительный экономический эффект [4]. К элементам такой системы относится поверхностная обработка почвы дисковыми орудиями.

Установлено, что дисковые рабочие органы унифицированной круглой формы не обеспечивают качественного резания почвенного пласта, т.к. в процессе работы перед диском сгруживается почвенно-растительная масса. В результате увеличивается тяговое сопротивление агрегата, снижается производительность, качество работы и нарушаются агротехнические требования. Часто возникают отказы в работе дисковых почвообрабатывающих агрегатов, случаются поломки.

Цель исследований: повышение эффективности работы дисковых почвообрабатывающих машин, снижение энергоемкости и повышение качества обработки почвы.

Объекты и методы

Методика теоретических исследований конструктивных параметров выпуклого шестиугольного диска предусматривала использование основных положений и законов классической механики, математики и статистики. В ходе исследований получена математическая модель выпуклого шестиугольного диска.

Результаты и их обсуждение

В ходе исследований выполнен расчет математической модели с целью выбора типа лезвия выпуклого шестиугольного диска [5]. Для упрощения расчетов в качестве математической модели выпуклого диска был принят круговой конус (рис. 1, а ), уравнение которого определяется по формуле [6]

z = ( R - V x ² + y² ) • tg ^e . ⁽¹⁾

Для получения математической модели необходимо в основание конуса вписать правильный шестиугольник и через каждые две соседние его вершины провести плоскость, параллельно оси ОZ. Таким образом, от воронки отсекаются сегменты (рис. 1, б ), а оставшаяся часть воронки и есть искомая математическая модель.

Пусть шестиугольник правильной формы А 0 А 1 А 2 А 3 А 4 А 5 вписан в основание конуса (рис. 1, б ). Рассмотрим случай, когда координаты начальной и конечной его вершин имеют значения:

A o (Rcos 30 ° , Rsin 30 ° ,0), A 5 (Rcos 30 ° , - Rsin 30 ° , 0), где R – радиус диска, мм.

При проведении плоскости параллельно оси ОZ через эти точки из конуса вырезается гипербола с уравнением

( z = ^R

к

^

³ R ² + y

При этом

(

h = R • 1

к

^

• tg ^e .

, 33 1

V • ^p .

Определим длину лезвия, т.е. длину дуги А 0 А 5 (рис. 1, б ):

R

L =-----f² cos β ⁰

x ² + ³R ² • cos² в

x2 + 3 R2

dx .

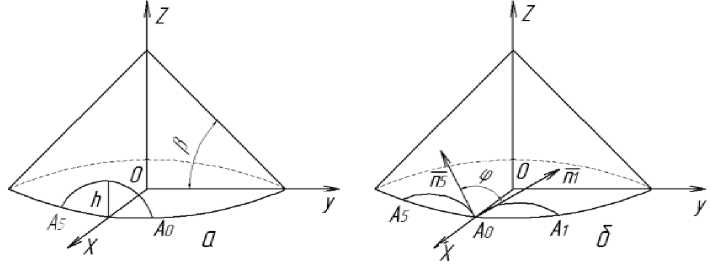
Рис. 1. Модель выпуклого дискового ножа: а – круглого; б – шестиугольного

При определении угла между лезвиями впишем шестиугольник А 0 –А 5 так, чтобы его начальная вершина лежала на оси ОХ, вершины (рис. 1, б ) будут иметь координаты: A (R, 0, 0), A i (Rcos 60 ° , Rsin 60 ° , 0), A 5 (Rcos 60 ° , - Rsin 60 ° , 0).

Исходящие из начальной вершины дуги можно описать параметрическими урав- нениями:

А 0 А 1 : x

= (1 -1) • R +1 • у, y = 1 •

—-—, z = R • (1 — V1 — 1 +12 )• 1дв,

, x R              R • л/3             /      /-----------.

А 0 А 5 : x

= (1 — 1 )• R +1 • — ,y = — 1 —-—,z = R • (1 — V1 — 1 +12 )• 1дв , где t изменяется от 0 до 1.

( dx dy dz )

Следовательно, для касательных векторов получим: I —,—,— 1 1 = 0 к d1 d1 d1 7

Таким образом:

n 1 =

R

к

R:^ , Ri^g ^ 1, _n,=f— R , — R ^³, Ri^g ^ 1

2       2 J ⁵ к 2      2       2 J

cos ф =

- 2 + tg ^{2 в} 4 + tg 2 в

1 - 3cos² в

1 + 3cos² в

ф = arccos

( Ь — Зсо^ ) [ 1 + 3cos² в J

На основании вышеизложенного получены значения стрелки лезвия ножа h , длины лезвия L и угла между касательными, проведенными к двум соседним лезвиям в их общей вершине φ (таблица). По полученным значениям построены графики зависимостей указанных величин от угла между образующей диска и его основанием ( β ) (рис. 2–4).

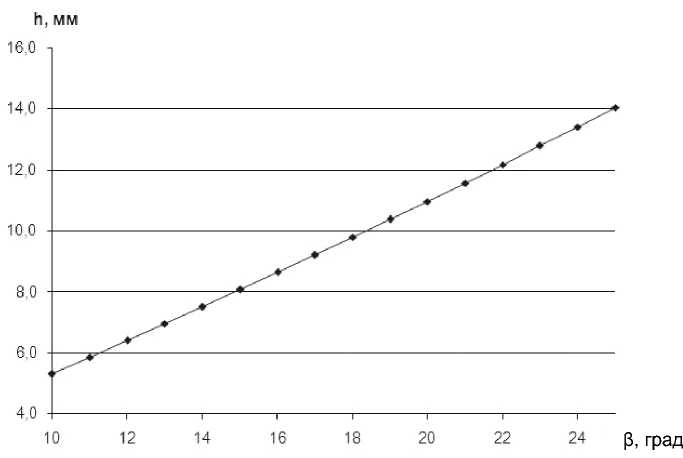
Рис. 2 . Зависимости стрелки лезвия ножа от угла между образующей диска и его основанием f = h(β)

Результаты расчетов параметров дисков

№ п.п.	β, град	h, мм	L, мм	φ, град	№ п.п.	β, град	h, мм	L, мм	φ, град
1	10,0	5,3	225,3	119,2	9	18,0	9,8	226,1	117,5
2	11,0	5,9	225,4	119,1	10	19,0	10,4	226,2	117,2
3	12,0	6,4	225,5	118,9	11	20,0	11,0	226,4	116,9
4	13,0	7,0	225,6	118,7	12	21,0	11,6	226,5	116,5
5	14,0	7,5	225,7	118,5	13	22,0	12,2	226,7	116,2
6	15,0	8,1	225,8	118,3	14	23,0	12,8	226,9	115,8
7	16,0	8,6	225,9	118,0	15	24,0	13,4	227,1	115,4
8	17,0	9,2	226,0	117,8	16	25,0	14,1	227,3	115,0

В рассматриваемой выше математической модели шестиугольного диска предполагалось, что секущие плоскости, вырезающие сегменты из конической воронки, проводились параллельно оси ОZ. Рассмотрим случай, когда секущие плоскости проходят через некоторую точку С с координатами (0, 0, Н). Считаем, что точка С либо лежит ниже основания конуса, либо выше его вершины

ππ

H = -R • Ідү, 0 < ү <— или H = R • Ідү, в < ү <— , где H – координата точки С по высоте; γ – угловая характеристика величины H.

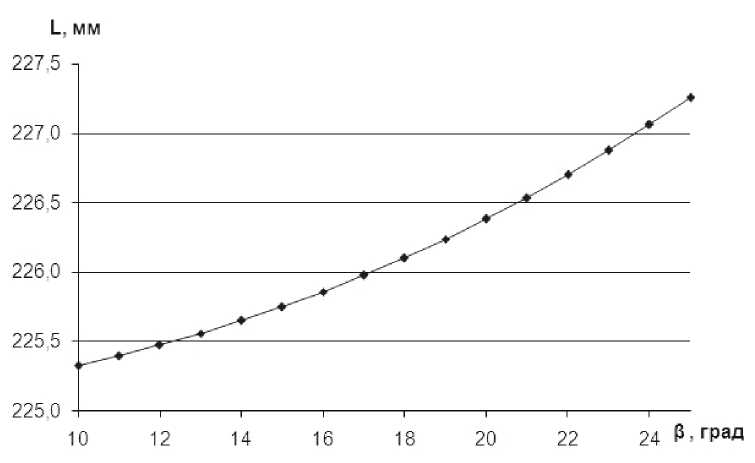
Рис. 3. Зависимости длины лезвия между двумя соседними вершинами от угла между образующей диска и его основанием f = L(β)

Ч, град

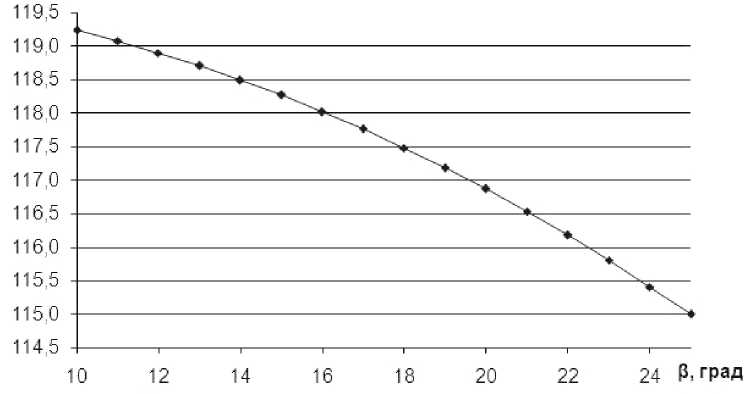
Рис. 4. Зависимости угла между касательными, проведенными к двум соседним лезвиям в их общей вершине от угла между образующей диска и его основанием f = φ(β)

Таким образом, к основным параметрам R , β добавим еще величину Н . Дуга А 0 А 5

(рис. 1, б ) теперь является линией пересечения поверхностей, заданных уравнением

z = H •

—

R •

• x

Аппликата точки с координатами (x, y, z), движущейся по указанной дуге, будет наибольшей при у = 0. Сравнивая правые части уравнений (1) и (2), получим

( R - V x ² + y ² ) • tge = H • 1 к

^“ -----

3 R

• x

Отсюда

x = ( H - R • tg P )

При таком х имеем z = h =

1----- tgP

H 2

( ^RA

• R • 1 -• tge.

V ² j

Из уравнения видно, что это предельный случай, полученный при H ^ да .

Решим уравнение относительно х . После соответствующих выкладок, которые опускаем, получим

1 -

x =

2     1 O L R o\ ² Г 4     1      2 „l 2

—+ — • tgP • J 1 tgP \ +I —уу • tg ² в I • y R V3 H N V   H J V 3 R ²   H ² J

-    • tgв

3 R ² H ²

.

Добавив сюда равенства y = y , z = H •

( 1 - 2 x А

V R • d3 J

, получим параметрическое зада-

ние дуги А 0 А 5 , когда роль параметра играет переменное у , изменяющееся на отрезке

—

R R T

,   . Тогда длина L лезвия равна:

2 2

R

L = 2 J V1 + Q ( y ) dy ,

I + ' . ]• tg- в^ y-

Q ( y ) =7----- ^{V 3} R H ^J---------

<1    R           Г 4      1      20 A ² 2

1 tg в +              gy     • y y

V H J V 3 R ² H ² J

.

Рассмотрим случай знака «–», соответствующий первой дуге (рис. 5).

R 3

Пусть ее параметризация: x = x ( t ), y =       , z = z ( t ), t e [ 0,1 ] .

Дифференцируя предыдущие равенства, имеем dz ,, ( 1 • dx 1    dyA

= H • dt V R • dt R V3 dt J

Тогда при t = 0 получим

dx        R

dt R

2 • I     • tg B - 1

V h

.

Следовательно, n 1 =

R     R V3  1 R • tgp

——------------.------.--- ——------------

R • tgp - 1  ^{2    2} R • tgp - 1

H              H J

Аналогичное равенство записываем для n ₅ , отличие лишь в знаке второй координаты. Следовательно

1 - 3 • cos ф =----

1 + 3 •

-

-

• cos² в

.

• cos² в

Таким образом, в представленной математической модели выпуклого шестиугольного диска рассмотрены три случая его изготовления, исходя из различного прохождения секущей плоскости m-m (рис. 5).

Рассмотрим первый случай, когда секущая плоскость m-m проходит параллельно оси OZ (рис. 5, а ); при движении диска в ходе обработки почвы его лезвие занимает горизонтальное положение, обеспечивая качественное подрезание пласта почвы средней плотности.

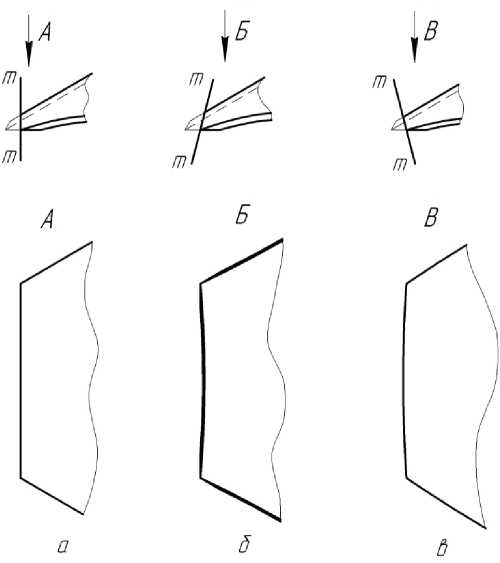
Рис. 5. Срез диска плоскостью m-m: а – параллельно оси OZ; б – через верхнюю вершину конуса; в – через нижнюю вершину конуса

Во втором случае плоскость m-m рассекает поверхность через точку, расположенную выше вершины конуса. Лезвие располагается на вогнутой кривой, его длина максимальна (рис. 5, б ). В данных условиях обеспечивается качественное подрезание рыхлого почвенного пласта.

Рассмотрим третий случай, когда секущая плоскость m-m проходит через точку, расположенную ниже основания конуса (рис. 5, в ); лезвие располагается на выпуклой кривой. Обеспечивается качественное подрезание твердого почвенного пласта.

Заключение

В результате теоретических исследований получена математическая модель выпуклого шестиугольного диска. Выявлены зависимости стрелки лезвия ножа (h), длины лезвия между двумя соседними вершинами (L) и угла между касательными, проведен- ными к двум соседним лезвиям в их общей вершине (φ) от угла между образующей диска и его основанием (β). Рассмотрены три случая изготовления выпуклого шестиугольного диска. В первом случае лезвие занимает горизонтальное положение, что обеспечивает качественное подрезание почвенного пласта средней плотности. Во втором лезвие находится на вогнутой кривой, создавая условия качественного подрезания рыхлого почвенного пласта, так как длина лезвия максимальна. В третьем – лезвие на выпуклой кривой и гарантирует качественное подрезание твердого почвенного пласта.

Omsk State Agrarian University named after P.A. Stolypin, Tara branch, Tara

Omsk State Agrarian University named after P.A. Stolypin, Omsk

Omsk State Agrarian University named after P.A. Stolypin, Tara branch, Tara

Model of the choice of a form of an edge of a convex hexagonal disk