Модели и методы календарного планирования сертификационных сессий в управлении проектами

НП «Ассоциация управления проектами «СОВНЕТ» основана в 1990 г., как профессиональная некоммерческая организация, действующая на основе Российского законодательства.

Основными направлениями текущей деятельности НП «Ассоциация «СОВНЕТ» являются:

• –    международная сертификация специалистов по управлению проектами по системе 4-L-C IPMA-СОВНЕТ;

• –    международная сертификация организаций по модели IPMA Delta;

• –    сертификация консультантов по управлению проектами по программе IPMA-СОВНЕТ;

• –    обучение, семинары и мастер-классы для специалистов проектного управления;

• –    членство в СОВНЕТ;

• –    аккредитация учебных программ;

• –    организация и проведение национального конкурса «Лучший проект года»;

• –    развитие деятельности молодежной ассоциации «YOUNG CREW СОВНЕТ»

Важной составляющей деятельности НП «Ассоциация «СОВНЕТ» является сертификация специалистов по управлению проектами, о ней поговорим более подробно в последующих разделах статьи.

Постановка проблемы

Процесс сертификации состоит из нескольких этапов, на каждом из которых осуществляется оценка кандидата [1]. Порядок проведения оценки на каждом этапе определен в зависимости от уровня компетентности А, В, С и D.

Порядок проведения оценки, объем решаемых задач, привлекаемые специалисты на каждом этапе определены в зависимости от уровня компетентности А, В, С и D, на который оценивается кандидат.

Одной из главных задач, требующих особого внимания, является составление расписания сертификационных сессий, при создании которого учитывается:

• –    возможность участия асессоров в определенные даты проведения сертификации;

• –    обязательность участия всех действующих асессоров в течение определенного временного периода в сертификационной сессии при условии минимального количества оцененных кандидатов;

• – наличие 1-го из 2 асессоров, имеющих опыт работы в сфере деятельности (отрасли), которую представляет кандидат на сертификацию;

  – соответствие назначаемых асессоров уровню кандидатов, участвующих в сертификации;

  – наличие свободной аудитории для проведения сертификации;

  – наличие экзаменатора установленной категории для данного уровня участников сертификационной сессии.

Для решения данной задачи рассмотрим использование моделей календарного планирования, поэтапно усложняя требования.

Модели календарного планирования

Рассмотрим ряд моделей календарного планирования и процесса сертификаций. Примем, что имеется база (список) из n асессоров, имеющих право проводить сертификацию и m претендентов на получение сертификата.

Модель 1. Определены даты сертификации и удобные дни претендентов. Известны возможности асессоров участвовать в сертификации в те или иные даты. Задача состоит в назначении асессоров на сертификационные сессии (по два асессора на каждую сессию) так, чтобы все сессии были обеспечены асессорами. Для формальной постановки задачи определим двудольный граф, состоящий из n + m вершин ( n вершин первого слоя, соответствующих асессорам, и m вершин второго слоя, соответствующих сертификационным сессиям).

Каждую вершину i первого слоя соединим с вершиной j второго слоя другой пропускной способностью 1, если асессор i может участвовать в сессии j .

Обозначим А i максимальное число сессий, в которых согласен участвовать асессор i , В i = 2 число асессоров, необходимых для проведения сессии j , Х ij = 1, если асессор i участвует в сессии j , Х ij = 0, в противном случае.

Задача 1. Определить Х ij , i = 1̅,̅ n , j = 1̅,̅ m

Ф( X )= I Ху(1)

(i, j >U при ограничениях

I Ху < Ai, i = 1?n,(2)

j U

I Ху = 2, j =1?m,(3)

i 'U где U - множество дуг графа, Ui - множество дуг, исходящих из вершины i первого слоя,

U ^– _j – множество дуг, заходящих в вершину j второго слоя.

Задача относится к классу транспортных задач (точнее к задачам о назначении), для которых существуют эффективные методы решения [2].

Пусть Х ⁰ – оптимальное решение задачи.

Теорема 1. Если ф ( х 0 ) = 2 m , то существует расписание сессий, при котором все сессии обеспечены асессорами.

Доказательство очевидно, поскольку каждому решению задачи соответствует некоторое расписание работы асессоров.

Пример 1 . Имеются 5 сессий и 4 асессора. В табл. 1 указаны возможности асессоров участвовать в сессиях.

Таблица 1

Возможности асессоров участвовать в сессиях

j i	1	2	3	4	5
1	1	1	1
2	1		1	1
3		1		1	1
4			1	1	1

Соответствующий двудольный граф приведен на рис. 1.

Примем А i = 3, i = 1̅,̅4.

Одно из решений приведено на рис. 1 (числа в скобках у дуг соответствует назначениям асессоров на сессии).

Если не удается обеспечить все сессии асессорами, то проводим опрос асессоров по их возможностям участвовать в той или иной сессии за дополнительную плату. Обозначим С _i j дополнительную оплату асессору i , если он согласен участвовать в сессии j , i = 1̅,̅ n , j = 1̅,̅m.

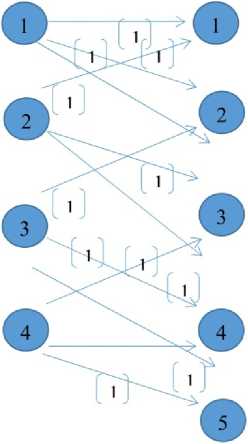
Рис. 1. Двудольный граф

Задача заключается в назначении асессоров на сертификационные сессии с минимальными дополнительными затратами. Задача является частным случаем транспортной задачи [2].

Дадим ее математическую постановку.

Задача 2. Определить Х ij , j = 1̅,̅ m i = 1̅,̅ n , минимизирующие

∑СijХij(4)

i,j при ограничениях

∑Хij = 2, j = 1̅,̅m,(5)

∑Хij ≤ Аi, i = 1̅,̅n.(6)

j

Алгоритмы решения транспортной задачи хорошо известны [2]. Покажем иллюстрацию одного из них на примере.

Пример 2 . Имеются 4 асессора и 5 сессий. В табл. 2 указаны дополнительные платы, при которых асессоры согласны участвовать в сессиях. Пусть А i = 3, i = 1̅,̅ n .

Таблица 2

j i	1	2	3	4	5
1	0	2	5	1	0
2	1	3	3	0	2
3	4	0	4	2	1
4	2	3	0	4	2

1-й шаг. На каждую сессию назначаем асессоров с минимальной дополнительной оплатой (рис. 2). Видно, что асессор 1 перегружен, а асессоры 3 и 4 недогружены.

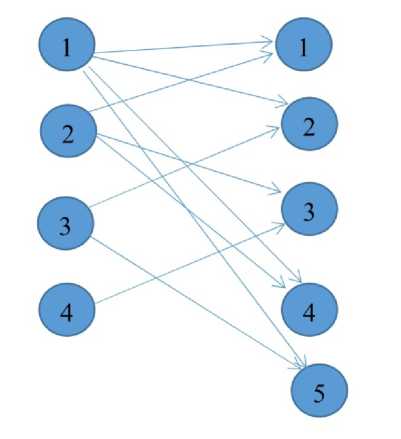
Рис. 2. Граф назначений

2-й шаг. Строим сеть, добавляя к графу (рис. 2) две вершины – вход 0 и выход Z . Вход 0 соединяем дугами длины 0 со всеми перегруженными вершинами. Все недогруженные вершины соединяем с выходом Z дугами длины 0. Длины дуг ( i , j ), соответствующих назначениям асессоров, полученных на шаге 1, получаем равными (– С ij ). Проводим дуги ( i , j ) длины С ij , идущие от вершин, соответствующих сессиям, к вершинам, соответствующих асессорам, назначены пунктиром на рис. 3.

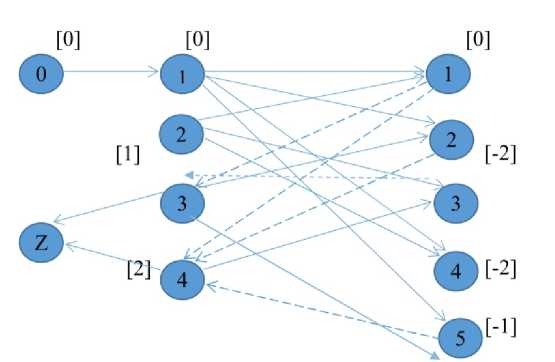
[-0]

Рис. 3. Граф назначений

3-й шаг. Определяем путь M минимальной длины из входа в выход [2].

4-й шаг. Корректируем назначение асессоров следующим образом. Если ( i , j ) М ( i -асессор, j -сессии), то отменяем назначение асессора i на сессию j . Если ( j , i ) М ( i -асессор, j -сессии), то назначаем асессора i на сессию j . Повторяем шаги 1̅,̅ n , если после корректировки остались еще перегруженные асессоры.

Пример 3. Рассмотрим сеть (рис. 3) с данными табл. 2. Установившиеся индексы вершин указаны на рис. 3 у вершин в квадратных скобках. Кратчайший путь М = (0, 1, 2, 4, z) имеет длину 1. Ему соответствует отмена назначения асессора 1 на сессию 2 и назначение на эту сессию асессора 4. Дополнительная плата составляет 9 единиц.

Модель 2. В модели 1 предполагалось, что сертификационные сессии не пересекаются во времени, так что асессор может принимать участие в любой из сессий, которые он указал. Если ряд сессий проводился одновременно, то, естественно, асессор может участвовать только в одной из них.

Для учета этого ограничения модифицируем двудольную сеть. Суть модификации покажем на графе рис. 1. Путь сессии 2, 3, 4 и сессии 4, 5 проводятся одновременно. Соответствующая модификация сети приведена на рис. 4. На этой сети решается задача 1.

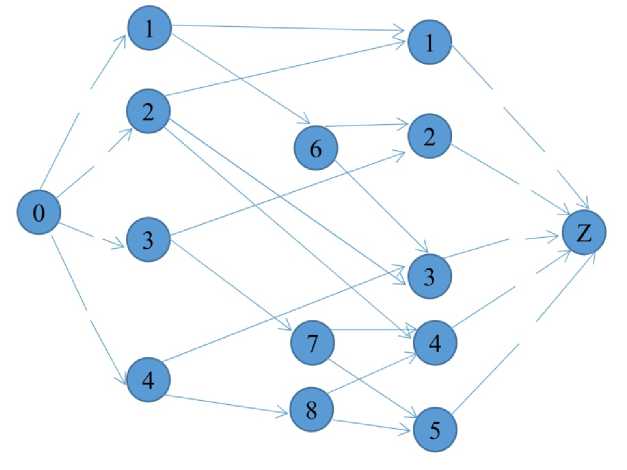
Рис. 4. Модифицированный граф

Поясним этот рисунок. Поскольку пропускная способность дуги (1, 6) равна 1, то асессор 1 не может участвовать одновременно в сессиях 2 и 3. Аналогично асессор 3 не может одновременно участвовать в сессиях 4 и 5 и асессор 4 не может одновременно участвовать в сессиях 4 и 5.

Для решения задачи превратим график в двудольную сеть, добавив две вершины вход 0 и выход Z (покажем пунктиром на рис. 4).

Вход 0 соединим с каждой вершиной i первого слоя дугой (0, i ) пропускной способностью А i .

Каждую вершину j второго слоя соединим с выходом Z дугой ( j , Z ) пропускной способности 2.

Задача свелась к определению потока максимальной величины в полученной сети [2]. Если поток максимальной величины насыщает выходные дуги (то есть равен 2m), то задача решена.

В противном случае вводим дополнительную оплату Асессоров за участие в сессиях, как в задаче 2.

Задача 3. Определить поток величины 2m с минимальными дополнительными затратами. Это известная задача определения потока минимальной стоимости в транспортной сети [2].

Модель 3. До сих пор предполагалось, что для каждой сессии определено место ее проведения. Однако для ряда сессий существуют альтернативные варианты проведения. Для учета этой ситуации будем рассматривать асессоров парами, каждая пара асессоров – это команда, которая может участвовать в сессии. Пара формируется на основе табл. 1, поскольку каждый асессор пары должен быть согласен участвовать в сессии.

Пример 4. Из табл. 1 следует, что в сессии 1 может участвовать только одна пара асессоров (1, 2). В сессии 2 тоже только одна пара – (1, 3), в сессии 3 могут участвовать три пары –

(1, 2), (1, 4) и (2, 4), в сессии 4 тоже три пары – (1, 3), (2, 4) и (3, 4). Наконец, в сессии 5 одна пара

(3, 4). В результате получаем двудольный граф (рис. 5).

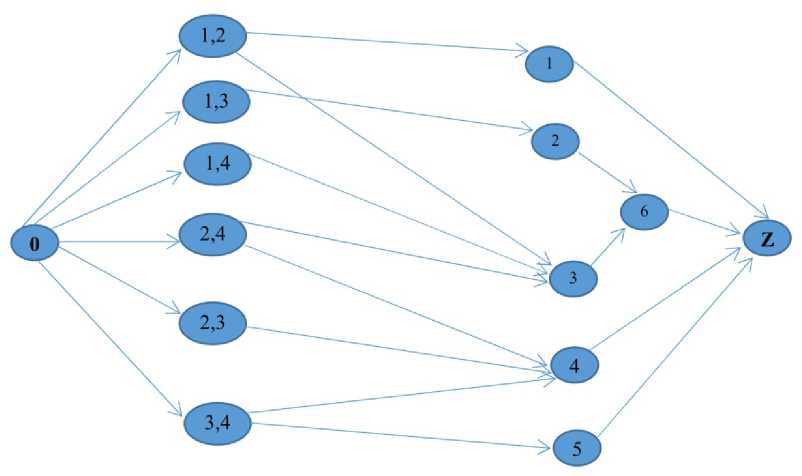
Рис. 5. Двудольный граф

Пусть варианты 2, 3 соответствуют альтернативным вариантам проведения сессии. Для учета этого обстоятельства вводим дополнительную вершину 6 такую, что пропускная способность дуги (6, Z ) равна 1, что исключает проведение сессии в двух местах.

Выводы

Использование моделей календарного планирования (различные модификации транспортных задач) позволяет построить реализуемые планы проведения сертификационных сессий с минимизацией затрат на оплату асессоров. При этом появляется возможность увеличить число сертификационных сессий. Предложенные модели учитывают различные ситуации, возникающие при формировании календарного плана, такие как невозможность проведения более одной сессии в одном месте, невозможность участия асессора в нескольких сессиях, если они проводятся в одно и то же время и др. Дальнейшие исследования предполагается проводить в направлении формирования программы повышения эффективности сертификационного процесса.