Модели, методы и средства организации учебного процесса с использованием уровневых дисциплин

Устойчивой тенденцией развития высшего образования является переход к инновационным формам обучения, реализующим индивидуальные образовательные траектории (далее – ИОТ) в учебном процессе. Благодаря этому становится возможным шире учитывать потребности и предпочтения обучающихся [1–6].

Уровневое обучение и его особенности

Один из способов реализации ИОТ заключается в организации уровневого обучения. Основной особенностью уровневых дисциплин является их адаптация к степени успешности освоения учебного материала обучающимися. В этом случае обучение ведется в различных подгруппах по отличающимся по сложности и объемам программам. Отнесение обучающихся к тому или иному уровню и, соответственно, переход в подгруппу соответствующего уровня осуществляются в течение семестра по результатам текущих контрольных мероприятий. В результате оказывается возможным регулировать уровни сложности задач и объемы заданий, которые предъявляются к обучаемым в той или иной подгруппе в процессе обучения.

Действительно, если предъявить всем обучающимся одинаковые по уровню сложности задачи и одинаковые по объему задания, рассчитанные на средний уровень текущей подготовки, то в результате их выполнения обучающиеся с высоким уровнем подготовки не смогут в полной мере повысить свой уровень знаний, умений и навыков, потому

Модели, методы и средства организации учебного процесса с использованием уровневых ...

Модяев Дмитрий Александрович

что потенциально могли бы решить более трудные задачи и выполнить задания большего объема. Обучающиеся с низким уровнем подготовки значительную часть работ не смогут выполнить. Тем самым они практически не приобретут умений и навыков, а тем более дополнительных знаний.

Сказанное выше можно также проиллюстрировать зависимостью, приведенной на Рисунке 1 [7].

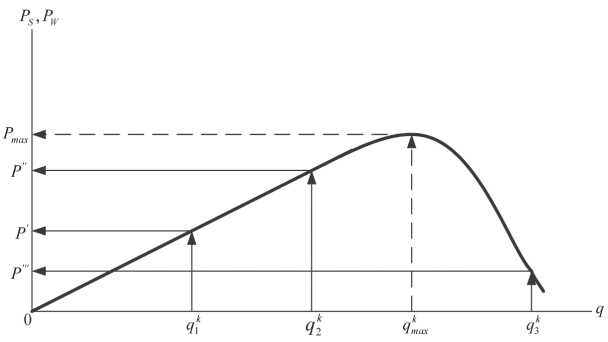
Рисунок 1. Изменение уровня умений и навыков обучающегося в зависимости от уровня сложности задач и объемов заданий

Источник: [7].

Здесь по оси ординат отложены значения уровней умений и навыков, приобретаемых обучаемым при проведении внелекционных видов учебных занятий (например, семинаров S и лабораторных работ W ). На оси абсцисс расположены значения уровней q сложности задач и объемов заданий, предъявляемых k -му обучаемому на семинарах и при выполнении лабораторных работ. Приведенная нелинейная зависимость качественно отражает процесс приобретения умений и навыков каждым из обучаемых. Отсюда следует, что повышение значения q (то есть интенсификация процесса обучения, увеличение учебной нагрузки на обучаемого) способствует повышению приобретаемого уровня умений и навыков. Действительно, при q₂^k >  q₁^k получаем P^'' >  P^' . При превышении значения q некоторого максимально допустимого значения эффективность процесса обучения резко падает. В результате при q₃^k >  q_m^k_ax получаем P^''' <  P^' . Такие режимы обучения в принципе недопустимы. Поэтому при выполнении обучаемыми вне-лекционных видов учебных занятий необходим индивидуальный подбор значения q^k

(близкий по значению к q₂^k ). Его конкретное значение будет обусловлено прежде всего уровнем знаний обучаемого.

В работе [7] приводятся экспериментальные данные, подтверждающие наличие в учебной группе обучаемых с различными динамическими характеристиками. Диаграмма (см. Рисунок 2) показывает группирование обучаемых по различным кластерам, различающимися моделями поведения. Здесь отражены типичные результаты статистического анализа знаний, приобретаемых обучаемыми на лекциях в течение семестра. На диаграмме в координатах (средний уровень знаний; среднеквадратическое отклонение уровня знаний) нанесены точки, соответствующие каждому из обучаемых, причем обучаемым различных кластеров присвоены разные обозначения.

0.35

О Кластер L1

□ Кластер L2

+ Кластер L3

х Кластер L4

+ Кластер L5

О Кластер L6

0.3-

О

ф

0.25

о 5

О ф о

ф

га

0.2

ф

0.15

0.2

0.3

0.5

0.6

□

+

0.8

Среднее значение уровня знаний по лекциям

Рисунок 2. Диаграмма распределения обучаемых по кластерам Источник: [7].

Из диаграммы следует, что обучаемым из кластеров L1, L2, обладающим стабильно высоким уровнем знаний, можно при выполнении практических занятий давать задачи повышенной сложности и задания увеличенных объемов. Обучаемым из кластеров L3, L4, отличающимся нестабильными параметрами обучения, возможно чередовать задачи повышенной и средней сложности и объемов. Следует отметить, что необходимо создавать дополнительную мотивацию таких обучаемых к повышению успешности обучения, – это позволит им переместиться правее по диаграмме. В определенной степени к этой группе обучаемых можно отнести часть кластера L5. Обучаемые из кластера L6 и оставшейся части кластера L5 обладают невысокой успешностью обучения и малой склонностью к ее изменению. Им следует предъявлять задачи невысокой сложности и малых объемов, но не ниже требований учебного плана.

Модели, методы и средства организации учебного процесса с использованием уровневых ...

Механизм обучения при использовании двух уровней

В этом случае в режиме ИОТ исходная группа обучаемых делится на две подгруппы, в которых обучение проводится раздельно: в одной подгруппе по программе основного уровня, а в другой – по программе углубленного уровня. Эти подгруппы образуют динамические группы, поскольку их состав может изменяться в процессе обучения. Механизм формирования динамических групп показан на Рисунке 3. Исходная группа из N студентов разбивается на две подгруппы численностью n ₁ и n ₂ , которые и образуют динамические группы. Исходный состав динамических групп в начале первого семестра формируется по результатам исходных отборочных мероприятий В, включающих анкетирование и тестирование студентов. В дальнейшем в процессе обучения будет возможен переход студентов между уровнями, что обусловливает изменение как состава, так и численности динамических групп.

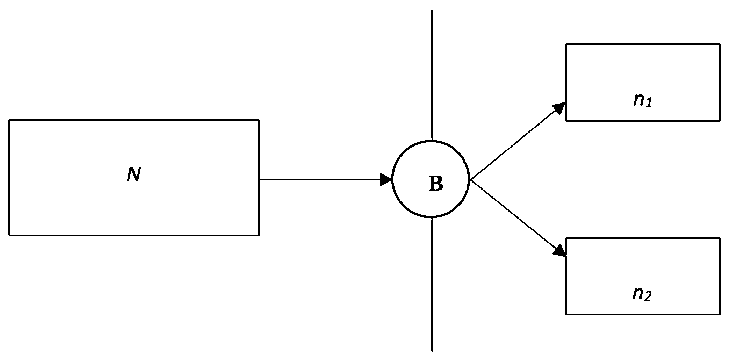
Рисунок 3. Формирование динамических групп Источник: здесь и далее рисунки выполнены автором.

Управление процессом обучения уровневой дисциплине заключается, во-первых, в предъявлении первой динамической группе в составе n ₁ студентов задач основного уровня сложности q _s1 и заданий основного объема q _w1 . Студентам, обучающимся во второй динамической группе по программе углубленного уровня численностью n ₂ , предъявляются задачи повышенного уровня сложности q _s2 и задания большего объема q _w2 . Выходными величинами P ₁ и P ₂ являются оценки результатов обучения в соответствующих динамических группах, что показано на Рисунке 4. Здесь отражена возможность переходов студентов из одной динамической группы в другую.

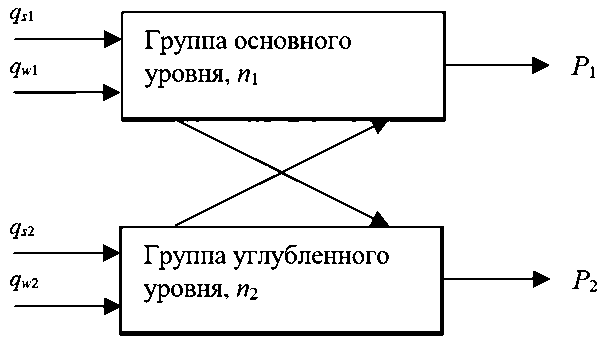
Рисунок 4. Управление сложностью задач и объемами заданий в динамических группах Источник: таблица составлена автором

Переходы студентов из одной динамической группы в другую и обратно в основном имеют место для обучаемых из кластеров L3 и L4.

Применительно к уровневой дисциплине «Информатика», имеющей два уровня (основной и углубленный), программа обучения представлена в Таблице.

По оценкам преподавателей, разрабатывавших задачи для уровневой дисциплины «Информатика», сложность задач углубленного уровня q _s2 превышает сложность задач основного уровня q _s1 примерно на 20 %, поэтому можно считать, что в относительных единицах на входе каналов управления сложностью задач имеет место соотношение q _s2 = 1,20 q _s1 . Количество заданий на углубленном уровне q _w2 , как следует из Таблицы, за четыре семестра обучения превышает количество заданий основного уровня в 1,18 раза. На входе каналов управления объемами заданий получим соотношение q _w2 = 1,18 q _w1 .

Тогда qs2/qs1 = 1,20; qw2/qw1= 1,18.                                     (1)

Таблица

Программа обучения

Основной уровень		Углубленный уровень
Содержание	Контроль	Содержание	Контроль
1-й семестр
Основы программирования на языке Си, ветвления, циклы. Вычисления, массивы и указатели. Функции, передача параметров, рекурсия	3 раздела, 10 тем, 20 заданий, 13 тестов	Основы программирования на языке Си, ветвления, циклы, оптимизация вычислений. Вычислительные методы. Массивы указатели, адресная арифметика. Функции, передача параметров, рекурсия. Символы, кодировки, строки и файлы	3 раздела, 10 тем, 20 заданий, 13 тестов
2-й семестр
Функции и массивы. Файлы. Сортировка массивов. Многомерные массивы. Структуры	3 раздела, 8 тем, 16 заданий, 11 тестов	Динамическая память. Сортировка массивов. Многомерные массивы. Векторные и матричные вычисления. Структуры. Динамические структуры данных. Списки, деревья, хеширование	3 раздела, 10 тем, 20 заданий, 13 тестов
3-й семестр
Структурированные динамические данные. Основы объектно-ориентированного программирования на языке Си++: классы и абстракции данных, наследование, полиморфизм	2 раздела, 8 тем, 16 заданий, 10 тестов	Объектно-ориентированное программирование на Си++. Перегрузка операций. Иерархия объектов и наследование. Виртуальные методы. Полиморфизм. Шаблоны и библиотеки	2 раздела, 8 тем, 20 заданий, 10 тестов
4-й семестр
Основы программирования на одном из языков высокого уровня: Python, C++, Fortran (по выбору)	2 раздела, 6 тем, 12 заданий, 8 тестов	Прикладное программирование на языках программирования высокого уровня: Python, C++, Fortran (по выбору)	2 раздела, 8 тем, 16 заданий, 10 тестов

Источник: таблица составлена автором.

Модели, методы и средства организации учебного процесса с использованием уровневых ...

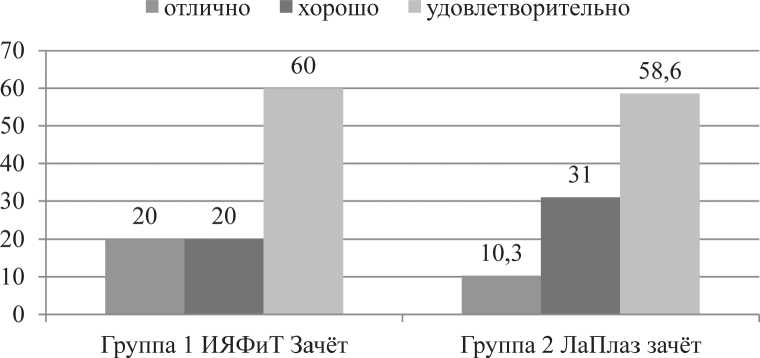
Обратимся к рассмотрению статистических данных уровневой информатики, полученных по итогам аттестации студентов на первом семестре в институтах ИЯФиТ (Институт ядерной физики и технологий) и ЛаПлаз (Институт плазменных технологий) НИЯУ МИФИ (см. Рисунок 5 а , б ). Итоговыми величинами здесь являются распределение студентов по степени успешности обучения и усредненные значения среднего балла по результатам аттестации при завершении семестра. Полученные значения среднего балла можно выбрать в качестве величин P ₁ и P ₂ .

Выберем приращение показателя Δ P в относительных единицах в качестве обобщённого показателя эффективности уровневого обучения. Поскольку вклад в итоговое значение величины P ₂ аддитивен, приращение показателя Δ P примет вид

∆P = ∆Ps + ∆Pw.(2)

Приращение, обусловленное влиянием первого канала в относительных единицах,

∆Ps= [ (qs2/qs1) P2/P1] – 1.(3)

Аналогично для второго канала получим:

∆Pw= [ (qw2/qw1) P2/P1] – 1.(4)

Исходя из данных Рисунка 5, для студентов ИЯФиТ значения P ₁ = 75,6 и P ₂ = 71,2 соответственно. Подставляя эти значения в соотношения (3), (4) с учетом (1) найдем значение обобщенного показателя эффективности уровневой дисциплины:

Δ P = Δ P _s + Δ P _w = (0,13+ 0,11)×100%= 24 %.

Аналогичные результаты имеют место при обучении уровневой информатике студентов института ЛаПлаз.

Доля студентов, %

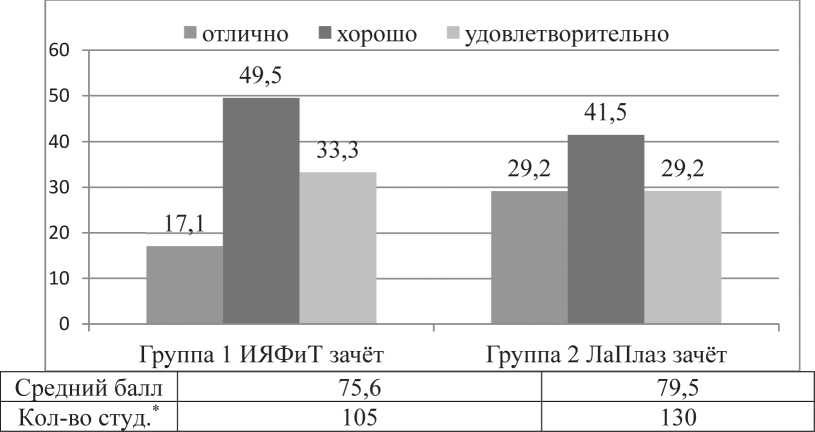
* — учитываются только студенты, успешно сдавшие зачет/экзамен с первой попытки

(без пересдач).

Рисунок 5 а. Статистические данные результатов обучения по информатике студентов основного уровня после окончания первого семестра (2023/24 учебный год)

Доля студентов, %

Средний балл	71,2	70,4
Кол-во студ.*	10	29

* — учитываются только студенты, успешно сдавшие зачёт/экзамен с первой попытки

(без пересдач).

Рисунок 5 b. Статистические данные результатов обучения по информатике студентов углубленного уровня после окончания первого семестра (2023/24 учебный год)

Заключение

Полученные практические результаты подтверждают правильность основных положений для разработки уровневых дисциплин и показывают эффективность их применения в учебном процессе

Отметим, что полученные результаты предполагают линейность в обоих каналах управления. Превышение учебной нагрузки студентов свыше допустимой может привести к возникновению нелинейных режимов, что отрицательно повлияет на процесс обучения.