Модели восприимчивости робота к псевдовоспитанию

В настоящее время ученые США, Канады, Швеции, Южной Кореи и Японии ведут активные исследования по созданию человекоподобных роботов-гуманиодов. Согласно прогнозам мировой рынок роботов-гуманоидов к 2018 г. должен составить 25,5 миллиардов долларов.

При создании таких роботов важным становится разработка математического аппарата и программного обеспечения, моделирующего "эмоциональную" сферу функционирования роботов-аналогов человека.

Так как создать точные копии эмоций человека у робота затруднительно и, наверное, невозможно, то к названию психологических характеристик робота, аналогичных психологическим характеристикам человека, будем в дальнейшем добавлять сочетание "псевдо-".

В работе [1] введено определение псевдовоспитания робота, основанного на испытываемых им псевдоэмоциях. В работе [2] введены понятия псевдовоспитательных уровней, характеризующих процесс псевдовоспитания робота при условии, что робот

испытывает только положительные псевдоэмоции.

В работе [2] впервые введены модели восприимчивости к песвдовоспитанию £ и относительной восприимчивости к псевдовоспитанию а робота, причем параметр а является безразмерной величиной и а е [ 0,1 ] . Согласно [2] восприимчивость к псевдовоспитанию £ равномернозабывчивого робота с равноценными эмоциями удовлетворяет соотношению

£ =

q

1 - О

- R,

где q – элементарное пседовоспитание ро-

бота, 9 - коэффициент памяти робота, R -псевдовоспитание робота, при котором происходит переход робота на следующий псев-довоспитательный уровень.

Задавая величину £ и вычисляя в процессе псевдовоспитания значение R , согласно соотношению (1) можно моделировать пе-

реход от первого псевдовоспитательного уровня на второй псевдовоспитательный уровень алгоритма Узнадзе [2].

Согласно работе [2] справедливо равен-

ство

а = ^^

q

.

В работе [3] введено условие перехода

от одного псевдовоспитательного уровня к другому, отличное от соотношения (1). Это условие формулируется следующим образом: "Переход с первого уровня на второй осуще-

ствляется, если справедливо равенство

1 - θ ⁱ     1 - θ ^{i - 1}

q     -q

1-θ    1-θ

= δ 1 ,

где δ – заданная малая величина, большая нуля, i – номер такта, при котором происходит переход на следующий уровень псевдовоспитания робота" [3].

Определим связь между величинами ε и δ .

Математические оценки восприимчивости роботов к псевдовоспитанию

Так как в настоящей статье рассматриваются равномернозабывчивые роботы с равноценными положительными псевдоэмоциями, то соотношение (1) можно записать в виде

q

1-θ

-ε=q

1 - θ ⁱ

1-θ

Прибавляя к равенству (3) равенство (4) и производя несложные преобразования, получим формулу

δ1 = q

_θ i - 1

1-θ

- ε .

Исходя из соотношения (5), очевидна справедливость неравенства

δ <  ^q - ε .           (6)

1   1-θ

Очевидно, что для перехода от одного псевдовоспитательного уровня к последующему уровню, должно выполняться соотношение δ >  0 . Исходя из этого неравенства и формулы (5), получим неравенство

ε < q

_θ i - 1

1-θ.

Переходя к термину относительной восприимчивости робота к псевдовоспитанию, с учетом соотношения (2), можно записать цепочку соотношений

_θ i - 1 q

α= ε <  1-θ = θi-1.     (8)

q 1

q 1-θ 1-θ

Таким образом, связь между величиной α , коэффициентом памяти θи порядковым номером такта i , при котором происходит переход на следующий   псевдовоспи- тательный уровень, определяется неравенством

α <  θ ^{i - 1} .                (9)

Заметим, что полученные оценки (4), (5), (7) и (9) могут применяться при задании исходных параметров в компьютерных программах,    моделирующих    псевдовос- питательный процесс робота при переходе с одного псевдовоспитательного уровня на другой псевдовоспитательный уровень [2].

Способ численной оценки восприимчивости человека к воспитанию

Предложим описание способа приближенной оценки величины восприимчивости человека к воспитанию, основанного на вышеприведенных формулах.

В работе [1] приведено описание программы SoundBot, моделирующей мимическую псевдоэмоциональную реакцию робота [4]. Согласно описанию функциональных возможностей этой программы она может использоваться при постановке голоса оратора.

Можно считать, что в качестве потенциального зрителя выступает робот с неабсолютной памятью [1], который способен проявлять свою псевдоэмоциональную реакцию на выступление оратора, подобную эмоциональной реакции человека-зрителя. Таким образом, методика постановки голоса сводится к следующим шагам [5]:

• 1.    Задание верхнего и нижнего порогов положительной псевдоэмоции робота, которые определяют диапазон громкости голоса, в который происходит постановка.

• 2.    Обучение. Оказание воздействия на робота звуковыми сюжетами до момента выработки только i положительных последовательно идущих друг за другом псевдоэмоций.

• 3.    Отдых (перерыв во взаимодействии с роботом).

• 4.    Тестирование постановки голоса (выработка первой положительной псевдоэмоции). На основе вышеописанной методики проведена серия экспериментов по постанов-

• ке голоса с испытуемыми, коэффициенты памяти которых определены ранее [5]. Результаты экспериментов представлены в таблице.

Таблица 1. Результаты экспериментов по постановке голоса оратора

№ экс.	P верх.	P ниж.	Кол-во непр. полож. тактов	Коэф. θ	№ ТППЭ1	№ ТППЭ2
1	80	10	20	0,7	5	2
2	80	10	20	0,9	4	1
3	80	10	20	0,7	5	3
4	80	10	20	0,9	2	1
5	80	10	20	0,6	3	1
6	80	10	20	0,9	4	3
7	80	10	20	0,8	4	3
8	80	10	20	0,9	3	2

*№ ТППЭ1 – номер такта первой положительной псевдоэмоции при обучении. № ТППЭ2 – номер такта первой положительной псевдоэмоции при тестировании

Как видно из табл. 1, при тестировании номер такта первой положительной псевдоэмоции меньше, чем при обучении, следовательно, можно говорить о некоторой постановке голоса на нужный диапазон громкости. Таким образом, проведенная серия экспериментов по постановке голоса показала возможность применения разработанных программных систем и методики для решения данной прикладной задачи.

Исходя из описанной методики постановки голоса оратора можно предложить способ приближенного определения величин а и s для человека при постановке его голоса.

Этот способ определяется следующими шагами:

• 1.    Задается количество требуемых непрерывных тактов i с положительными псевдоэмоциями.

• 2.    Используется описанная выше методика постановки голоса оратора.

• 3.    Если значение ТППЭ2 равно единице, то строится эквивалентный псевдовоспита-тельный процесс [1], на основе которого вычисляется величина q , иначе идти к 6.

• 4.    Вычисляется значение s по формуле (1) и величина а по формуле (2).

• 5.    Идти к 9.

• 6.    Делается длительный перерыв в экспериментах, который определяют специалисты-психологи и во время которого испытуе-

• мый забывает результаты прошедшего эксперимента по постановке его голоса.

• 7.    Увеличивается количество требуемых непрерывных положительных тактов i .

• 8.    Идти к 2.

• 9.    Конец.

Опишем другой способ приближенного вычисления численного значения а , основанный на математической теории эквивалентного псевдовоспитательного процесса робота [1, 5].

Пусть известны коэффициенты памяти человека и результаты измерений воспитаний (псевдовоспитаний) человека (робота). Тогда согласно работам [1, 5] для эмоций (или псевдоэмоций) можно построить эквивалентный воспитательный процесс с фиктивными тактами.

Для чередования тактов серии: "такты – фиктивные такты – такты" – формула воспитания человека (псевдовоспитания робота) Ri + j + k примет вид

1 — ^    +к 1 — ^

где i – количество первых тактов в серии, j – количество фиктивных тактов в серии, k – количество тактов в третьей очереди серии.

В работе [1] впервые введены модели восприимчивости к песвдовоспитанию s и относительной восприимчивости к псевдовоспитанию а робота, причем параметр а является безразмерной величиной и а е [0,1].

Используя табл. 1 и предполагая, что в результате завершения второго измерения воспитаний при получении первой положительной псевдоэмоции (столбец ТППЭ2) робот достигает псевдовоспитания, при котором происходит переход на следующий уровень алгоритма Узнадзе [2], можно записать cоотношение

q

-

0 k

- 0

+ 0+kq

1 - 0

1 - 0

£

1 - 0

из которого следует равенство

£ =

q    1 - 0

--q-----

1 - 0    1 - 0

-

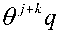
1-01 - 0 ’

Используя формулу (2) для вычисления относительной восприимчивости а к псевдовоспитанию с учетом соотношения (10), получим равенство

а = 0 (1 - 0J + 0i+ j). (11)

Анализируя равенство (11), можно сделать вывод о том, что при больших значениях i и j величинами 0 ^j и 0 ^{+ j} можно пренебречь и вычислять относительную восприимчивость к псевдовоспитанию по приближенной формуле

а = 0к.

Основываясь на результатах экспериментов, приведенных в табл. 1, и соотношении (11), можно вычислить величину а . Результаты расчетов приведены в табл. 2.

Таблица 2. Значения восприимчивости к псевдовоспитанию

№п/п	0	i	j	k	а
1	0,7	20	20	2	0,49
2	0,9	20	20	1	0,89
3	0,7	20	20	3	0,34
4	0,9	20	20	1	0,89
5	0,6	20	20	1	0,59
6	0,9	20	20	3	0,73
7	0,8	20	20	3	0,51
8	0,9	20	20	2	0,81

Анализируя табл. 2, можно сделать вывод о том, что большему коэффициенту памяти робота соответствует большая относительная восприимчивость к псевдовоспитанию (за исключением строки 5 табл. 2).

Согласно работе [5] психологические параметры, описываемые в табл. 1 и табл. 2, можно принять в качестве приближенных психологических характеристик человека, поэтому относительную восприимчивость к псевдовоспитанию робота можно при первом приближении принять равной относительной восприимчивости к воспитанию человека.

Заключение

Таким образом, в предлагаемой статье приведены математические модели характеристик восприимчивости робота к псевдовоспитанию и предложен способ приближенного вычисления этих оценок у человека и робота на примере постановки голоса ораторов.