Modeling of Air Temperature using ANFIS by Wavelet Refined Parameters

Published Online January 2016 in MECS

Human beings lifecycle in any area is mostly relying on the average air temperature. Owing to the above statement, the precise modeling of meteorological parameters like average air temperature is potentially required in both temporal and spatial a domain which is a most natural event for analyzing and making decisions in various application fields like climate monitoring, drought detection and environment issues [1]. To predict the energy consumption of passive solar buildings [2], prediction of room air temperature [3] and estimation of the residential building energy consumption [4]. A prior knowledge of such variation in air temperatures is essentially required. The accurate modeling of air temperature is also effective for analyzing the site suitability which is necessary for agricultural and forest crops. Any such variation of air temperature may lead to serious issues like change in rainfall patterns and also a rise in sea level.

Since average air temperature is one of the most fundamental elements of climate variation in area, an intense work has been earmarked to investigate the average air temperature behavior in a different time and location scales. Prediction of air temperature is one of the essential aspects in the fields of water resources planning and management, irrigation networks, tourism and everyday life issues.

Due to the dynamic nature of the atmosphere, it is truly difficult to predict ambient air temperature data accurately [5]. Various techniques like linear regression, auto regression, Multi Layer Perceptron, Radial Basis Function networks are applied to predict atmospheric parameters like temperature, wind speed, rainfall, meteorological pollution, etc. [5], [6], [7], [8], [9], [10], [11]. Recently, various soft computing techniques such as ANN, Fuzzy logic and Genetic algorithm are acquiring importance in predicting air temperature as these techniques can handle noisy, nonlinearity and uncertainty elements satisfactorily which placed as superior to the existing traditional methods.

Smith et al. [12] for accurate air temperature prediction developed and implemented respective tools based on Artificial Neural Network (ANN) model on using the data collected through 2005. ANN model was implemented for temperature prediction by Dombayc [13], which attempted to predict Daily means ambient temperature prediction using Artificial neural network method: A case study of Turkey was conducted by using previous daily mean temperature values to predict daily mean temperature for the present day using same model. Bilgili and Sahin [14] predicted long term monthly air temperature and rainfall based on ANN using Geographical variables (latitude, longitude, and altitude) and time, which were used as an input data for this approach. By such analysis it proves that ANN based model works better for prediction. Smith et al. [15] added seasonal information as the input pattern along with extra duration of data of 24 hrs. To predict air temperature models based on ANN. Hence the use of hybrid model such as ANN and fuzzy logic attracted researchers more because they had the capacity of handling non linearity and uncertainty in data set.

Pankaj Kumar [16] formulated weekly temperature forecasting using ANFIS (Adaptive Neuro Fuzzy Inference system), This model is used for forecasting the results at least a minimum of one week ahead of weekly temperature with the help of current weeks maximum mean weekly temperature as an order of input to predict. This formulation also included gbell type of membership function considering ten years data. By such analysis it proves that this model can be effectively used to obtain one-week ahead weekly temperature prediction. Later Daneshmand et al. [17] carried on a research to predict monthly minimum temperature data using ANFIS model with 42 years of statistical period data. They implemented the same approach by formulating the same model along with spectral analysis, correlation coefficient, and the knowledge of experts were used to select needed input parameters. Following with which the Results concluded that, this model is acceptable for prediction. Kisi et al. [18] used graphical input for prediction of long-term monthly air temperature. He tried to investigate the abilities of ANFIS model with Arificial Neural Network (ANN) in terms of results and found that ANN works better compared to ANFIS model. However, ANFIS is poorly capable to deal with noisy and highly varied seasonality behaviors of data like air temperature in terms of accuracy. To enhance the accuracy in prediction of air temperature, many methods were proposed. One of the recently popular methods is using data pre-processing such as stabilizing mean and creating stationary time series before putting them to any predictive model. Recently, Wavelet transform is widely used in data preprocessing techniques in non stationary and noisy time series. [19][20]

Wavelet analysis gives knowledge about the physical form of the data. This supplies a time frequency representation of a signal at many different periods in the time domain [21]. Wavelet model transforms the data from original time series to improve the ability of predicting by capturing useful information on various resolution levels [22], [23]. Wavelet decomposition is the one, which decomposes time series data into a different time and scale of wavelet transformation, and thus one can get the property of time series in different frequency bands as time goes by [24]. This method has been widely used in multi-scale analysis of time-series [25], [26]. Regularities of short-term (high frequency) and long-term (low frequency) reflect in different frequency bands after wavelet decomposition of time-series. Which includes many process changes by various time scales [27]. If Wavelet coefficients in different frequency bands are applied to ANFIS, the result of the hybridization has the possibility of improved time-series of different time scales, which can reflect its natural information better.

In recent time hybrid models are used in different fields like Harish et al [28] compared hybrid Particle Swarm Optimization based support vector machine model with single ANFIS model only for damage level prediction of non-reshaped berm breakwater and concluded that hybrid model works better compare to

ANFIS model alone. Moosavi et al. [19] investigated a hybrid Wavelet- ANFIS to forecast ground water level. In this study, it was proposed to compare hybrid model (wavelet-ANFIS) with single ANFIS and ANN models. But results showed that hybrid Wavelet-ANFIS model works better compared to single model. Partal and Kisi [20] used Wavelet and Neuro fuzzy for precipitation forecasting with the conventional single model. In terms of forecasting performance, hybrid model evidently outperformed other models.

From the literature review, it was observed that, there are hardly any hybrid models available with Wavelet transform and ANFIS which can handle the above mentioned limitations such as nonlinearity, noisy, uncertainty or even non stationary to certain extent for the modeling of air temperature. Hence this work is a novel approach in developing a hybridized wavelet-ANFIS model for modeling the average air temperature for different input scenarios. Furthermore, this study has assessed the effectiveness of hybridized Wavelet-ANFIS in terms of accuracy where results are compared with the single ANFIS model.

• II.    Data and Methodology

• A.    Input Data

  In the present work monthly recorded meteorological data from seven stations located in and around the Shimoga district (Fig. 1) (Shimoga station, Raypura station, Linganmakki station, Honnali station, Hiriyur station, B. R. Project and Davanagere) which covers a time period of 11 years (from January 2001 to December 2011) was used. Shimoga district covers an area of 8477.84 sq. km and lies in the western part of the Karnataka state between 13⁰27´ to 14⁰14´39´´ North latitude and 74⁰38´ to 75⁰45´ East longitudes. The district is surrounded by Uttara- Kannada & Dharwad districts in the north, Udupi & Chikmagalur districts in the south and Davanagere district in the east. The area belongs to the tropical climate region. Generally, the weather is hot and humid in the eastern part and very pleased with the remaining parts of the area. The evapotranspiration is normally higher in the ghat section as compared to plane areas in the east. Summer prevails between March to

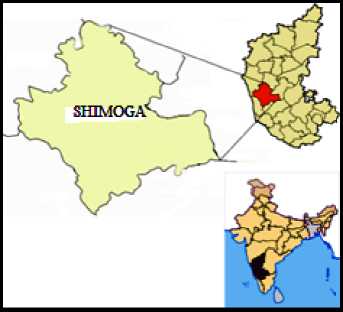
Fig.1. Study area early June, the wet months start from early June to September and during October and November months scanty rain is experienced by N-E monsoon. The winter commences in mid-November and ends in the middle of February. The maximum and minimum temperature of this area is 310 C and 180 C. Rapid growth of urbanization and vehicles are contributing in increase of temperature in recent time. The data were collected from January 2001 to December 2011 for a period of 11 years.

• B.    Methodology

In the present research work, the input for ANFIS model were the meteorological data rainfall, humidity, wind speed, sunshine hour, and the average temperature was used as output data for ANFIS model. Daubechies mother Wavelet was used to decompose the original meteorological data and the same was used as input for the ANFIS model but without changing the average temperature data which was used as output for the model. Finally, performance of accuracy of the model was compared between single ANFIS and hybridized Wavelet-ANFIS models. Flowchart of the procedure is represented in Fig. 2.

• C.    Wavelet Analysis

The Wavelet Series has been just like Continuous Wavelet Transform (CWT) and it requires a significant amount of time and resources, depending on the results required. Ψ (t) is the mother wavelet or the basis function (Eq. 1). The Continuous Wavelet Transform (CWT) is provided by Eq. (2), where f (t) is the signal to be analyzed. The transformation used in the wavelet functions are derived from the mother Wavelet through translation (shifting) and scaling (dilation) [29].

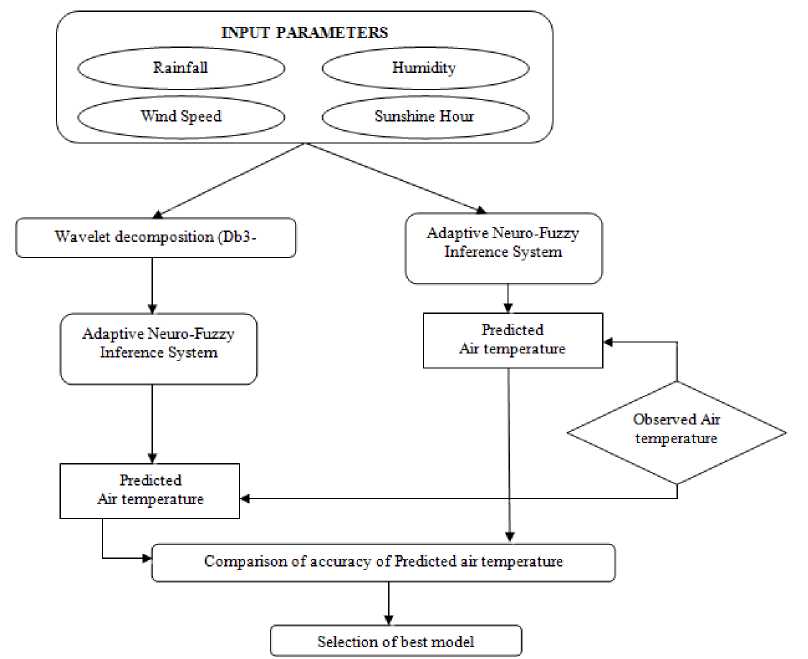
Fig.2. Flowchart of the work

Va ,b ( t )

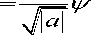
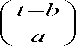
^Xwt ( a , b ) = -1= J f ( t ) .^ ^a

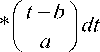
The Discrete Wavelet Transform (DWT), which is based on sub-band coding, is found to be best for computation of Wavelet Transform [30]. Implementation of this method is easy and works better in terms of computation time and resources required. DWT of f (t) can be written as (Eq.3);

Where ψa,b (t) is the successive wavelet, a is the frequency factor, b is the time factor and ψ* is the complex conjugate functions of ψ (t).

Xwt (j, k ) =

J f (t) V* ~tj - kbо dt

V ^a о        7

The most frequent choice of the parameters a0 and b0 is 2 and 1 time steps, respectively [30]. This power of two logarithmic scaling of the time and scale is known as a dyadic grid arrangement and is the simplest and the most efficient case for practical purposes [31].

DWT operates on two sets of function like high-pass and low-pass filters. The original time series is passed through high-pass and low-pass filters and separated at different scales. The time series is decomposed into one comprising its trend (the approximation) and one comprising the high frequencies and the fast events (the detail)( Fig. 3).

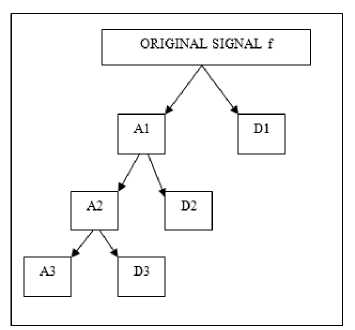
Fig.3. Architecture of Wavelet Decomposition model

• D.    The Adaptive Neuro-Fuzzy Inference System (ANFIS) model

ANFIS is a class of adaptive multilayer feedforward networks, applied to nonlinear forecasting where past samples are used to forecast the sample ahead. ANFIS incorporates the self-learning ability of neural networks with the linguistic expression function of fuzzy inference [32].

The ANFIS architecture is shown in Fig. 4. The ANFIS network contains five layers. Each layer contains several nodes described by the node function. Let Oijdenote the output of the ith node in layer j.

Layer 1 Each node in this layer is an adaptive node with node output defined as

O- = MAi( x),       for i=1,2—(4)

O' = Ит-2( У),     for i=3,4...(5)

In layer 2, each node π multiplies incoming signals and the output is the product of all the incoming signals.

Oi = ю. = ^Д (x)MB. (y), for i=i ,2(6)

Each node output represents the firing strength of a rule.

In layer 3, each node N calculates the ratio of the ith rules firing strength to the sum of all rules’s firing strengths.

O,³ = to , = —^-,       for i=1,2      (7)

to ₁ + to ₂

The normalized firing strengths are the output from this layer.

In layer 4, each node calculates the contribution of the ith rule to the overall output

O = to f = to ⁽ a i x ⁺ by ⁺ c i ) _fori=1,_{2       (8)}

Where to is the output of layer 3 and {a_i,b_i,c_i}is the parameter set. The parameters of this layer are known as consequent parameters.

In layer 5, the single node ∑ calculates the final output as the summation of all input signals

O ⁵ = overalloutput = ^ to , f

E ^to i f i

E to

Thus, an adaptive network is functionally equivalent to a Sugeno-type fuzzy inference system.[33]

• III.    Results and Discussion

To study the effectiveness of the approach, statistical comparison of measured and predicted values of training and testing processes were done and are shown in Table 1. The Correlation Coefficients (CC) between desired output and network predicted outputs were calculated by using Eq. 11.

The Root Mean Square Error (RMSE) and Scatter Index (SI) between target output and network predicted output is calculated by using Eq. 10 and Eq. 12.

Where x (or y) is the input to the node; and Ai (or Bi_2) is a linguistic label associated with this node. The membership functions for A and B are usually described by generalized bell functions.

RMSE =

n

'-E(о,— P,) *100% n i =1

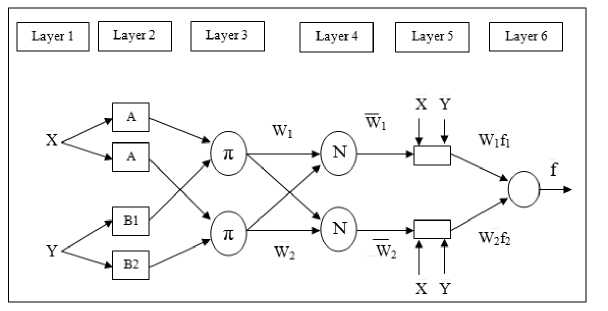
Fig.4. Architecture of ANFIS model

CC =

n

E po

= 1

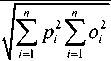
RMSE oi

Where, Oi and Pi are observed and predicted damage level respectively, n is the number of data set used and P _i &  O _i are average predicted and observed damage level respectively.

• A.    Anfis Model

In this study, monthly average observed meteorological data of 7 stations (132 months) were used. Among those 132 months of data of each parameter, we have classified to use 99 months data for training and 33 months of data are used for testing. Here the original data of parameters like rainfall, wind speed, humidity and sunshine hour are used for the input of ANFIS model (Sugeno first order with 16 fuzzy rules and gbell membership function) for both training and testing. Average air temperature data is used as output for both training and testing. Results are as shown in Table 1. In case of ANFIS model testing results; based on RMSE in degree centigrade, B.R.project station results are better although CC and SI are not encouraging with 0.286 and 2.60. Here accuracy mainly depends on the RMSE and it will be measured in terms of degree centigrade. When seven stations are considered, the overall results are less than 0.5 in case of CC, which reveals its poor performance. In regards with RMSE for testing, more than 6.6 which shows are very high values with low performance. Also in SI for testing, values are more than 0.03 which is not acceptable in terms of accuracy.

• B.    Wavelet-Anfis Model

After testing ANFIS model only, hybrid Wavelet-ANFIS model was also tested with the data for above mentioned seven stations. Original 132 months data is decomposed by db3 and level-3 function. Then Wavelet decomposed data is used as input for ANFIS model. Here hybrid Wavelet - ANFIS model works better because of combination of fuzzy logic, neural network and Wavelet transformation. When only in case of hybrid Wavelet-ANFIS model testing results, the station Linganamakki having better accuracy comparable to other station 0.954 in the case of CC, but in terms of RMSE and SI it is 0.71 and 0.027 respectively. But when the overall results of other stations are compared CC is more than 0.9. In regards with RMSE for testing less than 1.3 is very low value with high accuracy and also in SI for testing values are less than 0.03 which is better result in terms of accuracy.

Table 1. Statistical performance indices for different stations

SL.NO	STATIONS	MODELS	TRAINING			TESTING
			CC	RMSE	SI	CC	RMSE	SI
1	SHIMOGA	ANFIS	0.906	0.886	0.033	0.097	20.980	0.810
		Wavelet+ANFIS	0.946	0.674	0.025	0.939	0.960	0.037
2	HONNALI	ANFIS	0.934	0.770	0.030	0.438	85.200	3.310
		Wavelet+ANFIS	0.964	0.574	0.022	0.958	0.852	0.033
3	B.R.PROJECT	ANFIS	0.909	1.200	0.051	0.280	6.640	0.260
		Wavelet+ANFIS	0.960	0.835	0.034	0.952	1.362	0.055
4	DAVANGERE	ANFIS	0.940	0.740	0.027	0.520	10.160	0.380
		Wavelet+ANFIS	0.960	0.622	0.023	0.950	0.942	0.035
5	LINGANAMAKKI	ANFIS	0.890	0.550	0.021	0.160	31.890	1.20
		Wavelet+ANFIS	0.960	0.336	0.012	0.954	0.710	0.027
6	HIRIYUR	ANFIS	0.840	1.340	0.055	0.409	6.700	0.270
		Wavelet+ANFIS	0.965	0.683	0.025	0.942	1.012	0.038
7	RAIPURA	ANFIS	0.890	1.340	0.050	0.409	6.705	0.270
		Wavelet+ANFIS	0.958	0.848	0.035	0.950	1.339	0.054

• C.    Comparison of ANFIS Model and Hybrid Wavelet-ANFIS Model

Among two models, hybridized Wavelet-ANFIS shows good results in terms of statistical measures like a CC, RMSE and SI for observed and modeled data. Table 1 shows the comparative study of two proposed models and the table clearly depicts that hybridized Wavelet-ANFIS model outperforms ANFIS model with a higher CC of 0.9 when compared to CC of ANFIS model which is 0.5. Hybridized wavelet-ANFIS model has less than 1.3 RMSE values in both training and testing; whereas ANFIS model have more than 6.6 RMSE values for some stations. Also, the SI is less than 0.03 for the testing data of hybridized Wavelet-ANFIS model, but SI is more than 0.03 for ANFIS model.

The results of the hybridized model for the testing dataset can be observed in Fig.5 to Fig. 11 for the seven stations. It is observed from the figures that the modeling of temperature in different stations by the hybridized model is good with a CC greater than 0.9 in all the stations for testing data sets. The highest CC is obtained from Honnali station with a value of 0.958. In the analysis, pre-processed Daubechies mother wavelet up to 3rd level data was used as input for the ANFIS, which decomposes the original data leading to the removal of noise from the data which improved the results. From the Fig.12 to Fig. 18 it can also be observed that there are some differences between the observed and the modeled data. This difference is acceptable because of uncertainty in the nature.

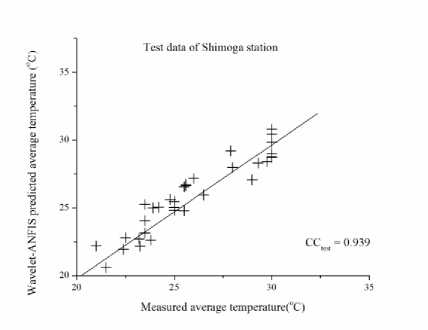
Fig.5 . Test data of Shimoga Station

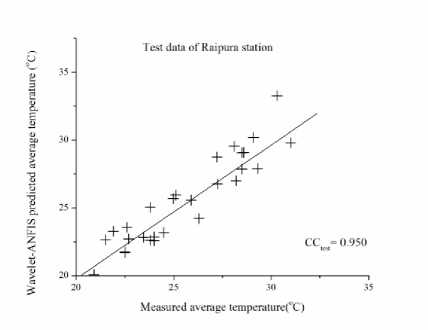
Fig.6. Test data of Raipura Station

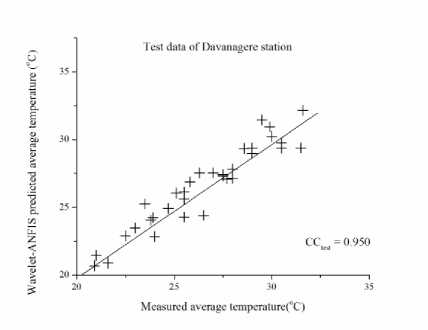
Fig.7. Test data for Davanagere Station

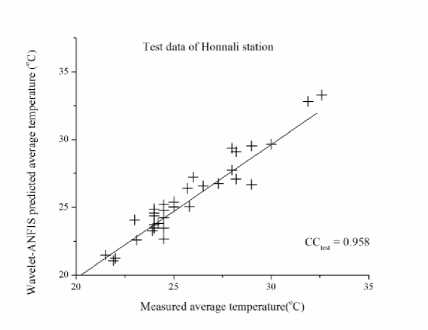
Fig.8. Test data for Honnali Station

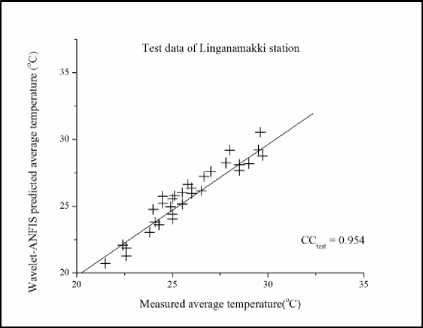
Fig.9. Test data for Linganamakki Station

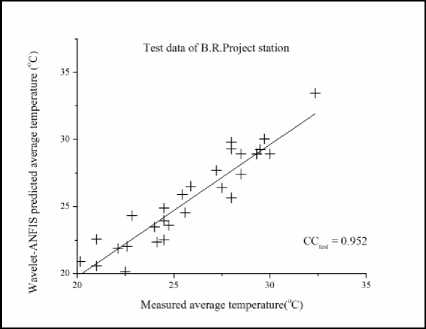
Fig.10. Test data for B.R. Project Station

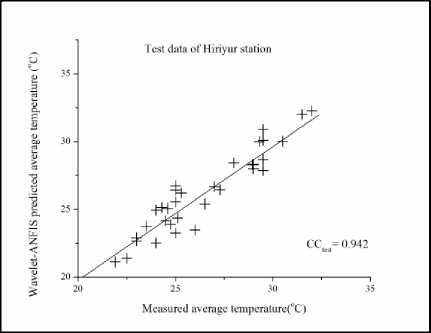
Fig.11. Test data for Hiriyur Station

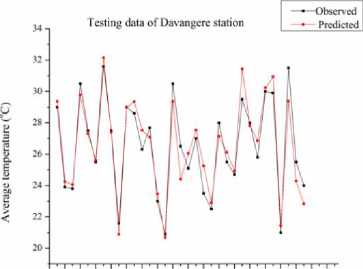
From the Fig.12 to Fig.18 it can be observed that the peaks in the measured data are modeled well by the hybridized Wavelet-ANFIS model. Some of the higher peaks of temperature are under-estimated by the model, whereas the lower peaks are over-estimated by the same model. By taking the meteorological data as a reference, modeled values have an overall 5% error. This error is acceptable because of uncertainty in the nature. Therefore, it could have some under/over estimation.

Considering individual stations, the modeling of average air temperature in BR Project, Honnali, Hiriyur and Raipura stations is better with the peaks being modeled accurately. The modeled values in Davanagere station are in agreement with the measured values during the initial months of up to 10. For later months the modelled value is either over-estimated or underestimated. When it comes to Shimoga and Linganamakki stations the average air temperature is under modeled after 16 months.

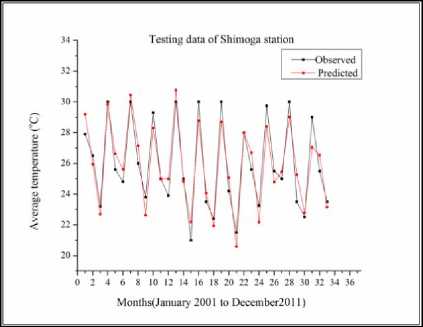
Fig.12. Hybrid Wavelet-ANFIS performance for temperature modeling of test data for Shimoga station

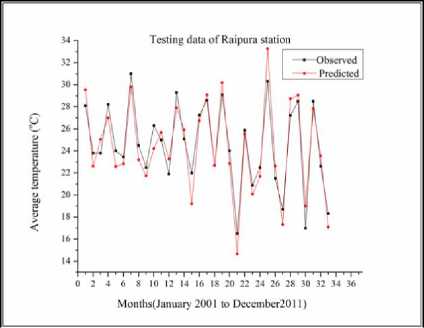
Fig.13. Hybrid Wavelet-ANFIS performance for temperature modeling of test data for Raipura station

О 2 4 6 3 10 12 14 16 IS 20 22 24 26 28 30 32 34 36

Months(January 2001 to December2011)

Fig.14 . Hybrid Wavelet-ANFIS performance for temperature modeling of test data for Davanagere station

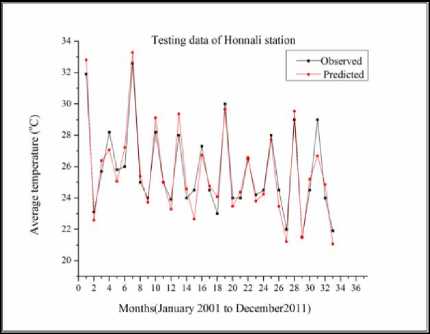
Fig.15. Hybrid Wavelet-ANFIS performance for temperature modeling of test data for Honnali station

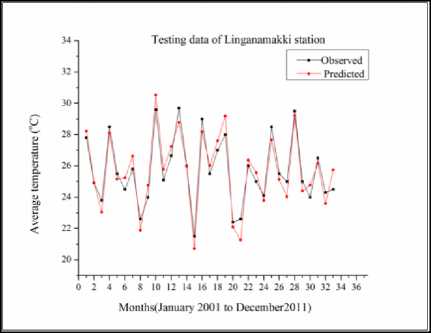
Fig.16. Hybrid Wavelet-ANFIS performance for temperature modeling of test data for Linganamakki station

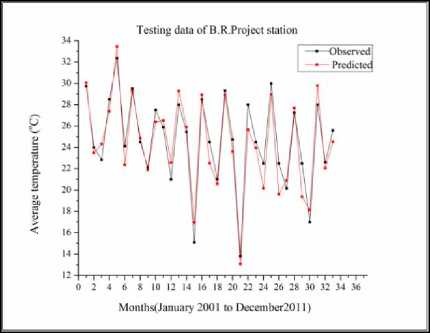
Fig.17. Hybrid Wavelet-ANFIS performance for temperature modeling of test data for B.R. Project station

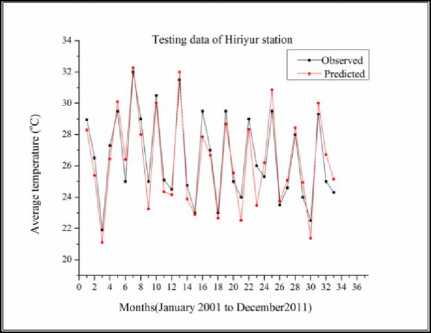
Fig.18. Hybrid Wavelet-ANFIS performance for temperature modeling of test data for Hiriyur station

• IV.    Conclusions and Future Research Directions

In the present work, Hybrid approach is proposed to modeling of precise average air temperature of meteorological variables by combining Wavelet and ANFIS models. Initially, observed data that were collected from stations like rainfall, humidity, wind speed and sunshine hours were used as inputs, while average air temperature (estimated from observed data) was obtained as output for the ANFIS model. Such obtained results from the ANFIS model revealed inferior performance due to higher nonlinearity and irregular seasonal behaviors of data. In the next stage, a novel hybrid approach was tried by using db3 level ‘L-3’ Wavelet, which transforms data for pre-processing original data like rainfall, humidity, wind speed and sunshine hours. Such obtained preprocessed data were used as input to ANFIS model with similar output as used for earlier single ANFIS model.

The hybridized Wavelet-ANFIS model was established to be more superior with higher CC, lower RMSE and SI compared to previous ANFIS model alone. The Wavelet transformation component has improved the performance of hybridized Wavelet- ANFIS model because of removing noise in the original data. The decomposition levels play a significant role in the output of the model as Daubechies order 3 and level 3 influences the modeling performance. It can be concluded that the proposed Wavelet-ANFIS hybrid model can be considered as a better choice for the present analysis in modeling of air temperature. Further, in case of any increase in the number of rules instigated in the model may lead to consume more computational time, which is considered as a drawback for the model. Rendering or including excess information’s as inputs to the ANFIS model may reduce the generalization capability and dimensionality of the problem due to huge number of approximation and detailed coefficients generated by Wavelet transformations.

Also, degree of non stationarity in the time series is very much sensitive in generation of stationary series by Wavelet Transform, which needs special visualization of the raw data series. This work may be extended to other type of mother wavelets with different levels with more input combinations along with effective Wavelet coefficients of the given series.

• [1]    R. E. Abdel-Aal, “Hourly temperature forecasting using abductive networks,” Engg. Apps. of Artificial Intelligence , 17(5), 2004, pp. 543-556.

• [2]    S.A. Kalogirou, M. Bojic, Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy , 25(5), 2000, 479-491.

• [3]    I.H Yang, K.W. Kim, Prediction of the time of room air temperature descending for heating systems in buildings. Building and Environment , 39(1), 2004, 19-29.

• [4]    G.Mihalakakou, M. Santamouris,A. Tsangrassoulis, On the energy consumption in residential buildings. Energy and Buildings , 34(7), 2002, 727-736.

• [5]    N. R. Pal, S. Pal, J. Das, K.. Majumdar, SOFM-MLP: a hybrid neural network for atmospheric temperature prediction. Geoscience and Remote Sensing , IEEE Transactions on 41(12), 2003, 2783-2791.

• [6]    J.H. Min, Y.C. Lee, Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert systems with applications 28(4), 2005, 603-614.

• [7]    M.A. Mohandes, T.O. Halawani, S. Rehman, A.A. Hussain, Support vector machines for wind speed prediction. Renewable Energy 29(6), 2004, 939-947.

• [8]    P.S. Yu, S.T. Chen, I.F. Chang, Support vector regression for real-time flood stage forecasting. Journal of Hydrology 328(3), 2006, 704-716.

• [9]    S. Osowski, K. Garanty, Forecasting of the daily meteorological pollution using wavelets and support vector machine. Engineering Applications of Artificial Intelligence 20(6) , 2007, 745-755.

• [10]    W.Z. Lu, W.J. Wang, Potential assessment of the “support vector machine” method in forecasting ambient air pollutant trends . Chemosphere 59(5), 2005, 693-701.

• [11]    Y. Radhika, M. Shashi, Atmospheric temperature prediction using support vector machines . International Journal of Computer Theory and Engineering 1(1), 2009, 1793-8201.

• [12]    B.A. Smith, R.W. McClendon, G. Hoogenboom, Artificial neural networks for automated year-round temperature prediction, Computers and Electronics in Agriculture 68, 2009, 52–61.

• [13]    Ö. Altan Dombayc,M. Gölcü, Daily means ambient temperature prediction using artificial neural network method: A case study of Turkey. Renewable Ener gy, 34(4), 2009, 1158-1161.

• [14]    M. Bilgili, B. Sahin, Prediction of long-term monthly temperature and rainfall in Turkey. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects , 32(1), 2009, 60-71.

• [15]    B.A. Smith, R.W. McClendon, G. Hoogenboom, Improving air temperature prediction with artificial neural networks, International Journal of Computational Intelligence 3, 2006, 179–186.

• [16]    P. Kumar, Minimum Weekly Temperature Forecasting using ANFIS. Computer Engineering and Intelligent Systems 3(5), 2012, 1-5.

• [17]    H. Daneshmand, T. Tavousi, M. Khosravi, S. Tavakoli, Modeling minimum temperature using adaptive neuro-fuzzy inference system based on spectral analysis of climate indices: A case study in Iran. Journal of the Saudi Society of Agricultural Sciences , 2012.

• [18]    O. Kisi, J. Shiri, Prediction of long-term monthly air temperature using geographical inputs. International Journal of Climatology 34(1), 2014, 179-186.

• [19]    V. Moosavi, M. Vafakhah, B. Shirmohammadi, N. Behnia, A wavelet-ANFIS hybrid model for groundwater level forecasting for different prediction periods. Water resources management 27(5), 2013, 1301-1321.

• [20]    T. Partal, Ö. Kişi, Wavelet and neuro-fuzzy conjunction model for precipitation forecasting. Journal of Hydrology, 342(1), 2007, 199-212.

• [21]    I. Daubechies, The wavelet transform time-frequency localization and signal analysis. Information Theory, IEEE Transactions on 36(5), 1990, 961-1005.

• [22]    T. W. Kim, J.B. Valdés, Nonlinear model for drought forecasting based on a conjunction of wavelet transforms and neural networks. Journal of Hydrologic Engineering 8(6), 2003, 319-328.

• [23]    T. Rajaee, S. A. Mirbagheri, V. Nourani, A, Alikhani, Prediction of daily suspended sediment load using wavelet and neurofuzzy combined model. International Journal of Environmental Science & Technology 7(1), 2010, 93-110.

• [24]    G. Strang, T. Nguyen, Wavelets and filter banks. SIAM, 1996.

• [25]    X. Shao, Y. Xu, C. Yan, Wavelet analysis of rainfall variation in the Yellow River Basin. Acta Scientiarum Naturalium-Universitatis Pekinensis, 42(4), 2006, 503.

• [26]    Y. Jianqun, An Application of Continuous Wavelet Transforms to Precipitation Analysis in Shanghai during One Hundred Years [J]. Meteorological Monthly 2, 2001, 004.

• [27]    X. Liu, S. Yuan, L. Li, Prediction of Temperature Time Series Based on Wavelet Transform and Support Vector Machine. Journal of Computers 7(8), 2012, 1911-1918.

• [28]    N.Harish,S. Mandal, S. Rao, S.G. Patil, Particle Swarm Optimization based support vector machine for damage level prediction of non-reshaped berm breakwater. Applied Soft Computing , 27, 2015, 313-321.

• [29]    A. Yarar, A Hybrid Wavelet and Neuro-Fuzzy Model for Forecasting the Monthly Streamflow Data. Water Resources Management 28(2) , 2014, 553-565.

• [30]    S. Wei, J. Song, N.I. Khan, Simulating and predicting river discharge time series using a wavelet-neural network hybrid modelling approach. Hydrological Processes 26(2), 2012, 281-296.

• [31]    S.G. Mallat, A theory for multiresolution signal decomposition:  the wavelet representation. Pattern

  Analysis and Machine Intelligence , IEEE Transactions on 11(7), 1989, 674-693.

• [32]    Z. Yun, Z. Quan, S. Caixin, L. Shaolan, L. Yuming, S. Yang, RBF neural network and ANFIS-based short-term load forecasting approach in real-time price environment. Power Systems , IEEE Transactions on 23(3), 2008, 853858.

• [33]    J.P.S.Catalao, H.M.I. Pousinho, V.M.F. Mendes, Hybrid wavelet-PSO-ANFIS approach for short-term wind power forecasting in Portugal. Sustainable  Energy ,  IEEE

  Transactions on 2(1), 2011, 50-59.