Моделирование деформационных смещений инструмента относительно заготовки при точении

Введение. Исследованию и моделированию деформационных свойств подсистем режущего инструмента и обрабатываемой заготовки уделяется неизменное внимание [1-4]. Это связано с тем, что при анализе устойчивости процесса резания и автоколебаний необходимо, прежде всего, иметь модель деформаций вершины режущего инструмента относительно заготовки. Аналогичная проблема стоит и при изучении точности обработки, особенно в случаях, когда заготовка имеет значительные деформационные смещения, изменяющиеся вдоль траектории движения инструмента относительно заготовки. Во всех случаях деформационные смещения как вершины режущего инструмента, так и заготовки в точке контакта с ней вершины режущего инструмента определяются по отношению к несущей системе станка. В рассматриваемом случае – по отношению к его направляющим. Сложность вычисления деформационных смещений вершины режущего инструмента относительно заготовки заключается в том, что они формируются в результате накопления деформаций в пространстве всех конструктивных элементов подсистем инструмента и заготовки, расположенных между несущей системой станка и рассматриваемыми точками. При этом большое влияние на деформационные смещения оказывают свойства сопряжения конструктивных элементов. Конструктивная сложность и неопределенность деформационных свойств узлов сопряжения приводит к тому, что при математическом описании динамики процесса резания необходимо не только знать дифференциальное уравнение динамики, но и разработать методы идентификации всех параметров этой модели.

В общем случае для анализа динамики процесса резания используются пространственные конечномерные модели, приводящие к необходимости анализа следующего дифференциального уравнения [4]:

d 2XdX

m(X,5p,tp) —- + h(X,5p,tp)— + c(X,5p,tp) = F(X,5p,tp) + f (t),(1)

dtdt где m(X,5„,tp) = m,,(X,5„,tp)] , h(X,5„,tp) = [hs,k(X,5„,tp)] , c(X,5„,tp) = ^,k(X,5„,tp)] -соответственно функциональные матрицы инерционных и диссипативных коэффициентов, а также функциональная матрица формирования упругой составляющей сил в зависимости от вектора деформационных смещений и технологических режимов. Размерность матриц s,k = 1,2,...,6; X={X„X2,X3,X4,X5,X6}т - вектор упругих деформационных смещений вершины режущего инструмента (первые три координаты) и заготовки в точке контакта с ней режущего инструмента (последние три координаты);

F = {Fi( X, 5 p, tp), F2( X, 5 p, tp), F3( X, 5 p, tp), F4( X, 5 p, tp), F5( X, 5 p, tp), F6( X, 5 p, t р)}т - век-тор-функции динамической характеристики процесса резания, раскрывающие зависимость сил резания от упругих деформационных смещений инструмента и заготовки, а также от технологических режимов: величины подачи на оборот 5p и глубины резания tp при заданной скорости; f (t) = {f,(t), f2(t), f;(t), f4(t), f5(t), f6(t)}т - изменяющиеся во времени со- ставляющие сил резания, не объяснимые в координатах упругих деформационных смещений, которые интерпретируются как шум.

Нами поставлена задача математического моделирования, разработки алгоритмов идентификации и на этой основе – исследования свойств только одной функциональной матрицы c ( X , 5 р , t р ) = [ c , , k ( X , 5 р , t р ) ] .

Постановка задачи. На основе результатов исследований, а также с учетом анализа работ, проводимых многими учеными, можно сформулировать следующие наиболее важные свойства деформационных смещений для подсистемы режущего инструмента.

• 1.    Все модели должны учитывать пространственные деформации. Представление зависимости деформационных смещений от сил в скалярном виде, например, в виде одного параметра технологической жесткости, является неправомерным, так как в этом случае, в частности при изучении механизмов потери устойчивости, теряется информация о циркуляционных силах, принципиально влияющих на потерю устойчивости стационарных траекторий движения инструмента относительно заготовки.

• 2.    Эксперименты показывают, что при приложении к вершине инструмента внешней постоянной силы неизменного в пространстве направления существуют такие направления ориентации силы, которым соответствуют деформационные смещения этого же направления. Такие деформационные смещения являются коллинеарными. В общем же случае, кроме коллинеарных деформационных смещений, существуют ортогональные смещения, нормальные к коллинеарным. На рис.1 приведен пример диаграммы экспериментально полученных деформационных смещений в плоскости, нормальной к оси вращения заготовки для станка 1К62.

• 3.    При изменении знака внешней силы, особенно в области малых деформационных смещений, становятся заметными гистерезисные явления. Если ориентация сил меняется в пределах от - 20 ° до + 150 ° , а также при условии, что деформационные смещения рассматриваются в вариациях относительно некоторого установившегося предварительно напряженного состояния, то гистерезисные смещения практически отсутствуют. Эти случаи соответствуют естественным направлениям изменения сил резания в вариациях относительно точки равновесия, т.е. случаям, которые рассматриваются при изучении динамики процесса резания.

• 4.    По мере увеличения сил неизменного направления наблюдается тенденция уменьшения приращения деформационных смещений, вызванных одинаковыми приращениями сил. Таким образом, для малых деформационных смещений в окрестности равновесия их матрицы жесткости можно считать постоянными. Кроме этого, указанные матрицы являются симметричными, т.е. потенциальными.

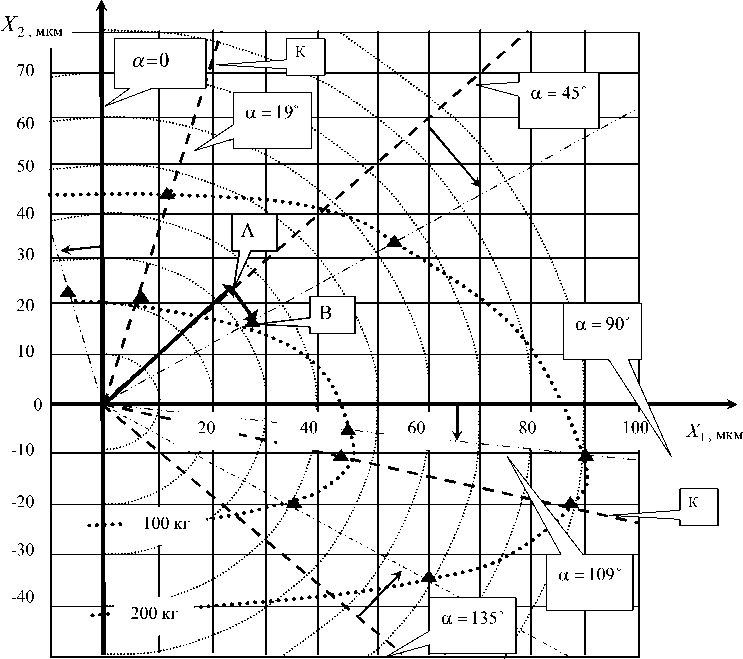
Рис. 1. Типичная диаграмма суммарных деформационных смещений вершины режущего инструмента в зависимости от направления и модуля внешней силы

На приведенной диаграмме стрелками показаны направления смещения ортогональных составляющих деформационных смещений (штрихпунктирная линия) по отношению к их коллинеарным составляющим (пунктирная линия). Из диаграммы видно, что существуют два направления приложения силы в рассматриваемой плоскости, которым отвечают только коллинеарные на- правления. Это направления, обозначенные «К». Угол между этими направлениями всегда равен п /2. Точечными кривыми показаны деформационные смещения, соответственно равные силам 100 и 200 кг. Важно подчеркнуть, что при одном и том же знаке силы только направления коллинеарных смещений (направления «К») практически не меняются. На приведенной диаграмме координата X 1 соответствует направлению, ортогональному оси вращения заготовки, координата X2 соответствует направлению скорости резания.

Приведенные свойства позволяют рассматривать деформационные смещения подсистемы инструмента в окрестности равновесия как идеальное упругое тело, а зависимость между силами и деформационными смещениями моделировать в виде:

сX = F ,                                       (2)

где X = { X 1 ,X ₂, X ₃}^т ; F = { F 1 ,F ₂, F ₃}^T ; с = [ c_s , _к ], s , к = 1,2,3 . Причем матрица с = [ c_s , _к ] - вещественна в силу гипотезы об идеальности упругого тела, симметрична и положительно определенна, т.е. потенциальна.

Для оценивания элементов матрицы с = [ c_sk ] в качестве исходной информации принимают траектории деформационных смещений вершины инструмента относительно несущей системы станка в зависимости от сил, имеющих в пространстве неизменную ориентацию. При этом используются алгоритмы скользящей линеаризации, рассматривающие оценки

с ( X * ) = [ d F_s / a X k ] _п ри: X = X . = [ с , , к ( X * )J s , к = 1,2,3 .                          (3)

Придавая силам измеримые приращения A F ⁽¹⁾ = { A F 1 ,0,0}^т A F ⁽²⁾ = {0, A F ₂ ,0}^{т A F (3)} = ^{ 0,0, ^{A F} 3^{} T} и измеряя вариации x Sk ) деформационных смещений, получаем системы для оценивания элементов матрицы с ( X * )

xэ с э( X *) = AFэ, (4) ■ x(1)    x 21)    x 31) 0000 0     0 " 0    0    0 x1(1)    x2(1)    x3(1)     0 00 0    0    0 0      0      0    x1(1) (1)        (1) x 2    x3 (2)      (2)      (2) x 1     x 2     x 3 0000 00 где xэ = 0    0    0 x1(2)   x2(2)   x3(2)     0 00 – матрица экспериментально опре- 0    0    0 0      0      0    x1(2) x2(2)   x3(2) (3)       (3)       (3) x1     x 2    x3 0000 00 0    0    0 x1(3)   x2(3)   x3(3)     0 00 _ 0     0     0 0      0      0    x1(3) x23'    xs31. деленных деформационных смещений; afэ = {AF1(1),0,0,0,af2(2),0,0,0,af3(3)}t - вектор изме- ренных внешних значений сил, действующих на режущий инструмент; cэ = {c 1,1,c2,1,c3,1,c 1,2,c2,2,c3,2,c 1,3,c2,3,c33} — вектор подлежащих оцениванию параметров матрицы жесткости.

Для фиксированного значения точки равновесия из выражения (4) получаем массив значений c i , j , i, j = 1,2,3 c i , j = c j , i при i * j , по которому получаем оценки параметров жесткости: их математические ожидания и дисперсии. Математические ожидания c € _{i , j} являются оценками матрицы жесткости c в системе координат OX ₁ X ₂ X ₃ (рис.2) для заданной точки равновесия. Для них также определяются дисперсии <€ i j , оцениваемые среднеквадратичными отклонениями.

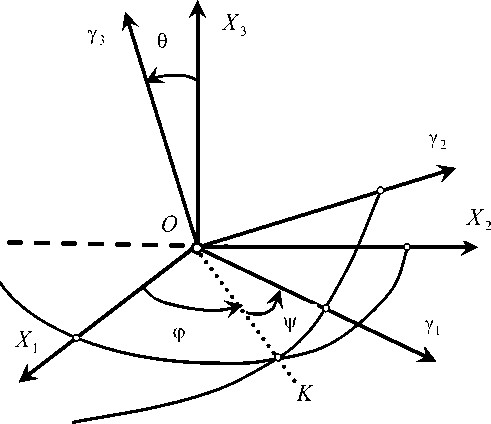
Рис.2. Система координат, в которой отсчитывается упругое деформационное смещение и внешние силы

Моделирование упругих деформационных смещений в линеаризованном виде, т.е. в виде матрицы жесткости, позволяет представить деформационные смещения в новой системе координат Oy 1 у ₂ у ₃ (см. рис.2), которая может быть получена на основе вращения системы координат OX 1 X ₂ X ₃ с помощью углов Эйлера. В новой системе O y 1 у ₂ Y ₃ матрица жесткости является диагональной.

Для определения матрицы линейного преобразования от системы координат OX ₁ X ₂ X ₃ к системе координат O y 1 у ₂ Y ₃ выполним три последовательных положительных вращения на углы Эйлера ф , 0 , ф вокруг осей OX ₃ , O y 1 , O y ₃ . В результате получим матрицу преобразования в

виде:

cos ф cos ф - sin ф cos 0 sin ф - cos ф sin ф - sin ф cos 0 cos ф

Л = sin ф cos ф + cos ф cos 0 sin ф - sin ф sin ф + cos ф cos 0 cos ф

sin 0 sin ф

sin 0 cos ф

sin ф sin 0

- cos ф sin 0 cos 0

Для обратного преобразования от системы координат O y 1 у ₂ у ₃ в систему координат

OX ₁ X ₂ X ₃ можно использовать следующую матрицу:

cos ф cos ф - sin ф cos 0 sin ф sin ф cos ф + cos ф cos 0 sin ф

Т = - cos ф sin ф- sin ф cos 0 cos ф - sin ф sin ф + cos ф cos 0 cos ф

sin ф sin 0 sin 0 cos ф

, ^Т = Л "* .

sin 0 sin ф

- cos ф sin 0

cos 0

Отметим некоторые свойства матрицы преобразования Λ : 1) Л^{- 1} = Л ^т ; 2) Л ^т Л = E -единичная матрица, поэтому матрица Λ является ортогональной. Кроме того, скалярное произведение векторов ( Л ' , Л ) = 1 , i = 1,2,3 , Л ' - вектор, элементами которого являются элементы i -го столбца матрицы Λ .

Связь старых координат с новыми определяется формулой:

X =Λγ , Δ F =ΛΔ F ^γ или γ= ΤX , Δ F ^γ = Τ Δ F .                  (7)

Подставляя формулу (7) в выражение (3), получаем:

c ^{( Y} ) y = A F ^{( y} ) , c ^(Y) =Л^{- 1} c Л .                                      (8)

Если для малых деформационных смещений в вариациях относительно точки равновесия оси ( Y 1 , y ₂, Y ₃)^т можно считать главными, то сила, имеющая направление, совпадающее с одной из осей ( Y 1 , Y ₂, Y ₃)^т , вызывает упругое деформационное смещение только в этом направлении. В данном случае матрица упругих деформационных смещений c ^γ является диагональной. Таким образом, задача заключается в том, что необходимо выбрать углы Эйлера в уравнении (8) так, чтобы матрица c ^γ была диагональной. Это можно сделать на основе решения уравнений c 'j ( ф , 0 , v ) = 0, ' * j , вытекающих из (8). Однако эта процедура для пространственного случая представляет большие сложности, так как полученные недиагональные элементы матрицы c ^{( Y )} из уравнений (8) являются сложными функциями от синусов и косинусов углов Эйлера.

Матрица жесткости c в статике является вещественной, положительной и симметричной. Для любой вещественной симметричной матрицы c существует такая ортогональная матрица Λ , что Л ^т c Л = c ^{( Y} ) , где c ^{( Y} ) = diag( X 1 , X ₂, X 3 ) - диагональная матрица, диагональными элементами которой являются собственные числа матрицы c , повторяющиеся согласно их кратности [5, 6].

Таким образом, можно привести симметричную матрицу жесткости c к диагональной форме, и вычислить матрицу преобразования Λ на основе определения ее собственных чисел и соответствующих им собственных векторов. При этом матрица жесткости c ^{( Y} ) = diag( X 1 , X ₂, X 3 ) в новой системе координат ( Y 1 , y ₂, Y ₃)^т имеет диагональные элементы, являющиеся собственными числами матрицы c .

Приведем более важный случай для матрицы жесткости c , когда она имеет различные собственные числа. Это естественный случай для подсистемы инструмента. Предположим, что матрица c имеет различные собственные числа X1, X2, X3, являющиеся решением характеристического уравнения det( c -X E) = 0.                                    (9)

Для каждого собственного числа X ' определим собственный вектор g‘ = ( g '1 ,g '2 ,g ' ₃)^т , который удовлетворяет системе уравнений

( c -X ' E ) g ' = 0 .                                       (10)

Собственные векторы g ¹ , g ² , g ³ , соответствующие различным собственным числам X 1 , X ₂ , X 3 , взаимно ортогональны.

Найдем по векторам g ¹ , g ² , g ³ нормированные собственные векторы e ¹, e ² , e ³ при условии ( e‘ , e‘ ) = 1 , i = 1,2,3 :

i gⁱ

e мг

Тогда ортогональная матрица преобразования Л , столбцами которой являются нормированные собственные векторы eⁱ ,

Л = ( e 1 , e 2 , e 3 ) =

e 1,1	e 2,1	e 3,1
e 1,2	e 2,2	e 3,2	.                                    (12)
_ e 1,3	e 2,3	e 3,3 .

Теперь можно определить углы ориентаций Эйлера путем сравнения элементов матриц (5) и (12)

cos 0 = e33, sin ф sin 0 = e 3 1, sin ф sin ф = e 1 3,

или

0 = arccos e-

ф = arcsin(

3,3 ,

e

3,1       ),

e 1,3

ф = arcsin(—     ,     ).

Деформационные свойства подсистемы режущего инструмента в плоскости. Эллипсоид жесткости для пространственного случая преобразуется в эллипс жесткости в плоскости (рис.3). Для этого случая можно сразу получить выражение для ориентации эллипса жесткости и значения его диагональных элементов.

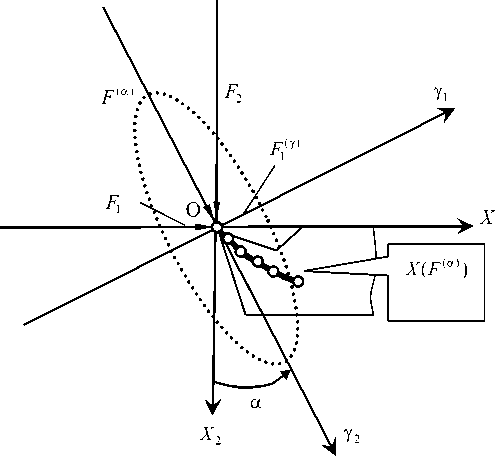
Рис.3. Система координат, в которой отсчитывается упругое деформационное смещение вершины режущего инструмента и внешние силы

Если идентифицированы матрицы упругих деформационных смещений с в пространстве

• X , то их выражения с ^{( Л )} в пространстве Л получаем на основе следующего преобразования:

с ^{( Л )} = А_{х а}сА_{х л} .

X ,Л X ,Л

Пусть в окрестности точки равновесия X * = { X ^ , X 2 }^т идентифицированы матрицы деформационных смещений x = { x , , x ₂}^т . Тогда для этой матрицы выполним преобразование (14) поворота координат

c ^{( Л )} =

cos a — sin a

sin a cos a

с 1,1

c 1,2

c ²⁴

^c 2,2 J

cosa sin a

— sin a cosa

( c , , cos² a + c _{2 2} sin² a — 2 c₁₂ sin a cos a ) [( c _{2 2} — c , 1 ) sin 2 a + c , ₂ cos 2 a ]

[( c _{2 2} — c 1 1 ) sin 2 a + c 1 ₂ cos 2 a ]

( c 1 1 sin² a + c _{2 2} cos² a + 2 c 1 ₂ sin a cos a )

.

Определим условия, при которых недиагональные элементы в матрице (15) были бы ны нулю [( c ₂ , ₂ — 0 1,1 )sin2 a + c ,,2 cos2 a ] = 0 , тогда получим:

рав-

^a = 2^arctg

^{2 c 1,2}

.

У ^c 2,2

—

^ci,i у

Матрица c ^{( Л} ) является диагональной, т.е.

c ^{( Л} ) =

с 0,1 0

,

где c ₀₁ = ( c 1 1 cos² a + c _{2 2} sin² a — 2 c 1 ₂ sin a cos a ) ; c _{0 2}

с 0,2 _

= ( c 1 1 sin² a + c _{2 2} cos² a + 2 c , ₂ sin a cos a ) .

Выполняя обратное преобразование координат { у 1 , у ₂}^т в x = { x , , x ₂}^т , получаем выражение для определения матрицы деформационных смещений вершины инструмента при заданной матрице (17):

c =

cos a

sin a

— sin a

соsα

с 0,1 0

cos a — sin a

( c 0,1 cos² a + c 0, ₂ sin² a )

c ₀ , ₂ - sin a

Г

2⁽ c 0,2

соsα

— c ₀ ,1 ) sin 2 a

|⁽ c 0,2 ^— c 0,1 ^{)sin2 a}

( c 0 1 sin² a + c 0 2 cos² a )

.

По мере увеличения внешних сил изменяются значения матриц жесткости. При этом ориентация эллипса жесткости практически не меняется.

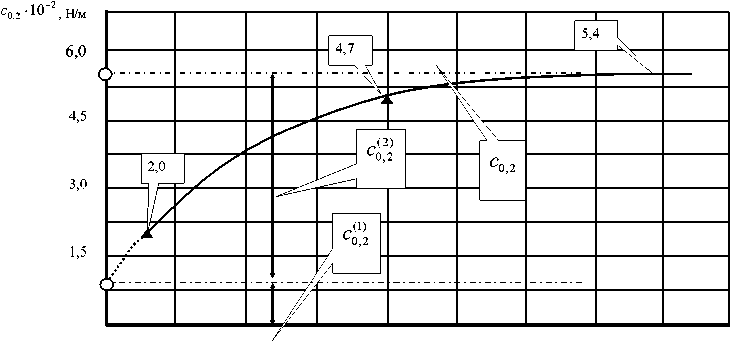
На рис.4 показаны зависимости жесткостей от координат { у 1 , у 2 }^т еЛ . Они хорошо аппроксимируются экспоненциальными функциями, т.е.

					<
с „,( У , )	(1) с 1,0	(2) + с 1,0	1 -	— exp	— у	у У
						М
с ^« ( У , )	(1) = с 2,0	(2) + с 2,0		— exp	— у	т (2) Y У_

,

(1)    (1)

где   с _1,0 , с _2,0

(2)   (2)

с 1,0 , с 2,0

– значения жесткостей на начальном этапе приложения внешней нагрузки;

– значения приращения жесткостей по мере увеличения деформационных смеще- ний; TY1),T'2: - параметры, характеризующие скорость увеличения параметров жесткости.

10 11

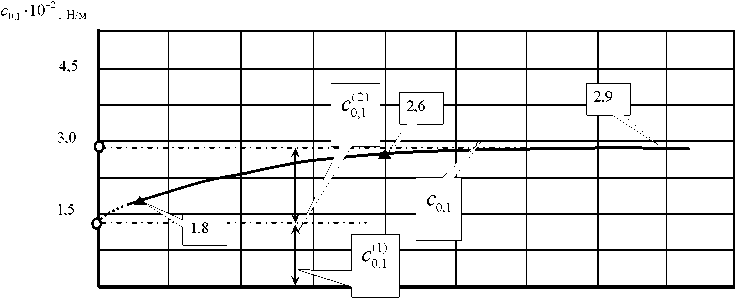
О                      20                   40                 60                  80 Ут- мкм

0                        10                    20                  30                   40    У2, мкм

Рис.4. Зависимость элементов матриц жесткости деформационных смещений вершины инструмента по направлениям ориентации эллипсов жесткости в зависимости от деформационных смещений по этим же направлениям

Практически полное соответствие экспериментальных и теоретических результатов связано с тем, что параметры матриц жесткости в направлениях { Y 1 , Y 2 } определены на основе идентификации. Однако они идентифицированы при анализе деформационных смещений по направлениям { F 1 ,0} и {0, F 2 } , а сами деформационные смещения вычислены по алгоритмам [см. формулы (15), (18) и (20)] при ориентации силы под углом 45 ° . Наибольшая погрешность, которая не превышает 10%, находится в области малых внешних сил. При больших силах (превышающих 500 Н) погрешность составляет 1-2%. Приведем также данные об основных параметрах, характеризующих деформационные свойства вершины режущего инструмента для различных станков токарной группы (см. таблицу). Поперечное сечение инструмента определяется следующими размерами: ширина основания – 30 мм, высота – 26 мм, вылет инструмента приведен в таблице.

Параметры упругих характеристик подсистем инструмента для различных станков

Тип станка	с 0,1 - 10 —2 , н/м	с 0 2 - 10 2 , Н/м	α , град	Вылет инструмента l , мм
1К62	2,9	5,4	10	50
1К62	1,7	5,1	18	120
УТ16Ф3	4,3	6,7	12	50
16К20 с УЧПУ NC210	3,7	6,5	14	54
1В340Ф30	2,8	4,5	19	54

Данные таблицы показывают, что параметры, характеризующие деформационные смещения, зависят не только от типа станка, но и от параметров режущего инструмента, в частности, от его вылета из зажимного приспособления. Нетрудно показать, что при этом увеличение упругих деформационных смещений вершины режущего инструмента в направлении X ₂ возрастают существенно больше, чем деформации стержня инструмента. Здесь вновь приходится считаться с тем, что за счет увеличения вылета инструмента возрастает момент вращения, поворачивающий всю суппортную группу, а также перераспределяется нагрузка на отдельные элементы. Ориентация осей существенно влияет на область устойчивости динамической системы резания, рассматриваемой в вариациях относительно точки равновесия.

Особенности деформационных свойств подсистемы заготовки. Главными особенностями деформационных смещений заготовки являются следующие:

• –    зависимость матрицы жесткости от траектории движения суппорта вдоль оси вращения заготовки;

• –    практически равные значения жесткостей по направлениям ориентации эллипсов жесткости (рис.5). Поэтому, исходя из уравнений (19), матрица жесткости всегда является диагональной для любой ортогональной системы координат, расположенной в плоскости, нормальной к оси вращения заготовки. В этом случае для определения упругих деформационных свойств подсистемы заготовки достаточно знать распределение жесткости вдоль оси вращения заготовки;

• –    при рассмотрении проблем устойчивости процесса резания и многообразия, формируемых в окрестностях стационарных траекторий, необходимо дополнительно анализировать не только движения центра масс заготовки, но и крутильные деформационные смещения. В этом случае необходимо учитывать крутильную жесткость всей подсистемы привода вращения заготовки.

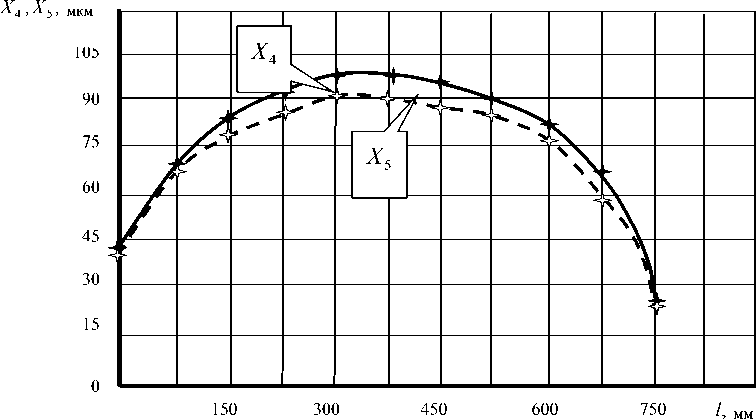
Рис. 5. Зависимость деформационных смещений точки на заготовке вдоль оси ее вращения (заготовка закреплена в трехкулачковом патроне и поджата вращающимся задним центром).

Параметры заготовки: длина 750 мм, диаметр 80 мм, сталь 45

Выводы. Приведенные математические модели упругих деформационных свойств подсистем режущего инструмента и обрабатываемой заготовки позволяют учитывать главные особенности деформаций вершины режущего инструмента и заготовки в точке их контакта. При изучении преобразования траекторий движения суппорта в траекторию формообразующих движений инструмента относительно заготовки необходимо учитывать деформации вершины инструмента в пространстве, т.е. для каждой точки равновесия упругие деформационные смещения инструмента должны 1013

рассматриваться в виде квадратной матрицы жесткости деформационных смещений размерности 3 x 3. При этом для анализа деформационных смещений подсистемы заготовки достаточно иметь информацию о распределении скалярной величины жесткости по длине, дополненную данными о крутильной жесткости. Приведенный формализм и методика параметрической идентификации в равной мере может быть распространена на другие технологические процессы обработки на металлорежущих станках.

Основные результаты исследования получены при финансовой поддержке РФФИ по проекту 07-09-90000.