Моделирование динамического взаимодействия балки и стержневого основания под действием подвижных нагрузок

Исследуемые в статье конструкции расположены на деформируемом упругом основании, то есть на таком основании сооружения, деформируемость которого учитывается при расчете опирающегося на него элемента другой конструкции. К ним на деформируемом основании относятся: фундаменты промышленных, гражданских и сельскохозяйственных зданий и их комплексов, аэродромные и дорожные покрытия, рельсы и шпалы железнодорожных путей и т.д.

Обьекты и методы исследований

Известно, что большинство моделей расчета конструкций на упругом основании достаточно подробно разработано лишь для статических задач. Однако существует ряд задач, исключающих статическую трактовку и делающих необходимым исследование динамических процессов при изгибе балок и плит на деформируемом основании. Проектирование зданий и сооружений на современном этапе невозможно без учета динамических воздействий, присущих таким мезанизмам, как подъемные краны, различного рода строительное оборудование, компрессорные установки, производственные взрывы и др.

Особенностью данной задачи при движений груза с постоянной скоростью является возможность стационарного режима движения, при котором прогиб под грузом все время остается постоянным. Общая картина изгиба оси балки будет неизменной, но равномерно движущейся со скоростью системы сил и как бы сопровождающей эту систему. Таким образом, в подвижной системе координат, связанной с движущейся системой сил, движение будет неустано-вившимся, прогиб оси балки будет зависеть только от новой координаты x и не будет зависеть в явном виде от времени t .

Рассмотрим вначале действие сосредоточенной силы, движущейся с постоянной скоростью по балке, лежащей на стержневом основании. Тогда уравнение изгиба оси балки запишется в виде [5]

Э⁴ u    d ² u

IE —? + P— 2" + d x 0      d t 0

bE₀ d u a о ^d t 0

= ^P ( x 0 , t 0 )

xt где 0 и 0 - переменные в неподвижной системе координат.

Подвижную систему координат свяжем с движущейся силой (рис. 1). Переменные в новой и старой системе координат будут связаны следующими соотношениями.

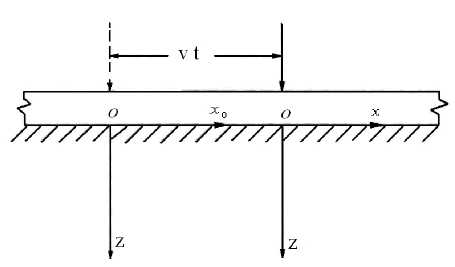
Рисунок 1 - Действие системы сил движущихся по балке бесконечной длины с постоянной скоростью.

Для записи производных в подвижной системе координат имеем dku _ dku du дк = dxd dt 0

du   v du   d ² u _ d ² u  ^ 2 d ² u

∂t ∂x   ∂ t ₀ ²    ∂ t ²      ∂ x ²

Имея ввиду независимость u от t , из (1) для прогиба оси балки, получим обыкновенное дифференциальное уравнение 4-го порядка

IE d ⁴ u     d ² u    bE du

ρ dx ⁴      dx ²      a ₀ dx

_ 0

Граничными условиями для которого будут в точке приложения силы d3uл_ P _d3un u л^ un dx3   2 IE dx3

,.

Отметим, что здесь уже нельзя принимать условия равенства нулю тангенса угла наклона касательной к прогибу, поскольку нагрузка подвижная и нет никакой симметрии относительно точки приложения силы.

На бесконечности du _ 0 u _ 0 dx

,.

Характеристическое уравнение дифференциального уравнения (2) имеет два неотрицательных действительных и два комплексных корня с отрицательной действительной частью

, _ A + B ,V3

EbV- ( i ± Q ) ) q = i 2 IEa ₀

+

ρ

3 IE

A + B >  0 ^Q >  ⁰

,,

A • B

_V 2 _ρ

В силу граничного условия на бесконечности для описания движения балки в правой относительно точки приложения силы части можно воспользоваться только двумя решениями, соответствующими двум комплексным корням, а для левой части - решения соответствующего положительному корню u л = C1 e (A+B)x

A + B

x

^U n = e ²

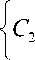
A - B cos 2

3Xx + C ₃ sin

A - B

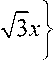
С учетом условий в точке приложения силы, получим [1], [2], [3], [4]

u л(x) =

2IE ( a+b )3

e ( a + в ) x

Фл( x ) =

P 1

2 IE ( A + B ) 2

e ( a + в ) x

Mл( x )

P      e (A + B ) x

) л ( x ) =- P e' A ^{+ BB}

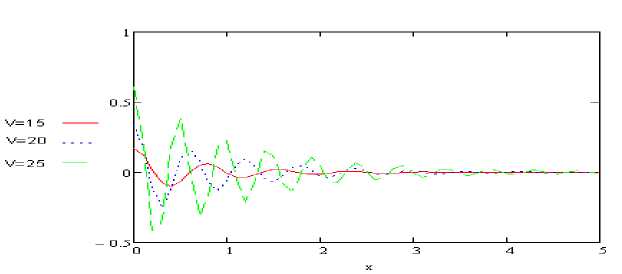
Рисунок 2 – Графики u (x) при различных значениях скорости V.

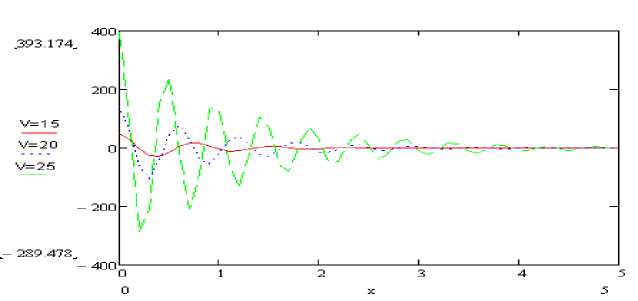
Рисунок 3 - Графики М (x) при различных скорости V.

Вывод:

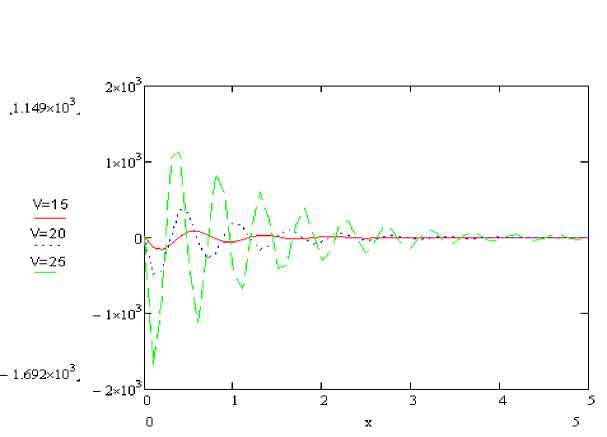
Рисунок 4 – Графики Q (x) при различных скорости V.

P u„ =     e n 2IE

(A+B A x 2

1------------- a

[(A+B)

A - B R cos----- 3x x +

A - B

sin

( A + B ) 3 ( A - B )     2

3 x r ,

P

^{Ф п} 2 IE ( A + B ) 2 e

(A+B )r x 2

A - B

cos

V3 (A2 + B2)

sin

A ²

- B ²

A - B

,

P n = 2 (A + B)2 e

. (A+ B! x J 2 ( A ² + B² )

+ AB

(A+B)

A - B cos

—

A 3   . A - B sin

( A - B )     2

На основе полученных формул проведен численный расчёт на компьютере.

На рисунках 2-4 представлены значения прогибов и внутренних силовых факторов, вычисленных по полученным формулам. В случае действия двух или нескольких сил воспользуемся методом суперпозиции.

Выводы

Получены численно-аналитические решения этих задач, на основании которых разработаны вычислительные алгоритмы, позволяющие производить расчет таких параметров прочности балки, как величина прогиба, скорость прогиба, внутренних силовых факторов.

Задача о движении груза по балке, лежащей на упругом основании, является актуальной при расчете и проектировании многочисленных инженерных сооружений: аэродромных и дорожных покрытий, шпал и рельсового пути, наплавных мостов и других конструкций.