Моделирование гидродинамики жидкого металла в ячейке МГД-сепаратора

Выделение отдельных компонентов из металлических расплавов является частой технологической задачей во многих технологических процессах химической или металлургической промышленности, а также в энергетике. Необходимость в таких операциях возникает при обогащении руд, рафинировании металлов или переработке вторичного сырья. Очищенный металл обладает повышенной механической прочностью и однородностью физических свойств, что играет значительную роль при производстве и эксплуатации изделий. Другим важным примером является очистка жидкометаллических теплоносителей в ядерной энергетике, где накопление включений примесей, создающееся в процессе эксплуатации, критическим образом сказывается на безопасности процесса и сроке службы оборудования. В новейших реакторах на быстрых нейтронах в качестве теплоносителя используются жидкие металлы, в частности натрий. Жидкие металлы, как теплоносители, химически активны. Состав примесей, и присутствующих в исходном натрии, и появляющихся в процессе эксплуатации установок, разнообразен. Так, кислород в составе оксидов натрия в большей степени аккумулируется при ремонтных работах и из защитного газа [1] . Даже малейшее (10 ^-6 –10 ^-4 %) содержание окислов в натрии приводит к ухудшению его теплофизических и электрических свойств. В первом случае ухудшается теплоотвод и нарушается тепловой баланс системы охлаждения, а во втором — понижается эффективность работы насосов, перекачивающих теплоноситель [2, 3] .

В основе всех методов разделения лежит различие физических свойств отдельных компонентов смеси: температуры плавления или кипения, плотности, электроотрицательности, диффузии в жидкой и твердой фазах и так далее. Традиционными на сегодняшний день методами очищения от примесей являются флотация инертными газами [4] (пропускание через водную взвесь или расплав руды пузырьков газа, увлекающих частицы примеси за счет сил поверхностного натяжения), направленная кристаллизация, электролитические методы, механическая фильтрация и долговременное отстаивание расплава руды либо ее взвеси в жидкости [5] . В последнем случае руду смешивают с жидкостью заданной плотности и добиваются всплытия/осаждения частиц примеси. Таким образом, разделение компонентов смеси происходит под действием сил тяжести и плавучести. Недостатком большинства существующих методов является их высокая энергозатратность и экологическая нагрузка на окружающую среду. С другой стороны, многие из них не могут быть вписаны в современную идеологию создания непрерывных технологических процессов в реакторах проточного типа. С этой точки зрения поиск методов разделения смесей металлов в расплавах, основанных на иных физических принципах, является актуальной задачей современной науки.

Статья опубликована в открытом доступе по лицензии CC BY 4.0

Эффективность разделения компонентов смеси за счет сил тяжести и плавучести можно повысить путем влияния на эффективную плотность рабочей жидкости посредством внешних полей [6] . Это могут быть накладываемые на проводящую среду скрещенные электромагнитные поля, либо индукционные с чисто магнитным воздействием. Реализующие их устройства называются МГД-сепараторами. Пример такого устройства — магнито-жидкостный сепаратор, в котором внешнее магнитное поле позволяет контролировать эффективный вес жидкости посредством частичного уменьшения/увеличения силы тяжести [7] . В силу высокой стоимости и относительно малого рабочего диапазона температур магнитных жидкостей данный метод используется преимущественно при обработке руд драгоценных металлов.

Электропроводящие среды, помещенные во внешнее постоянное/переменное магнитное поле, при пропускании через них тока под действием электромагнитных сил меняют свою эффективную плотность. Идея повышения результативности разделения компонент смеси за счет повышения эффективной разности плотностей несущей жидкости и примесных включений предложена еще в середине прошлого века [8] . В электропроводной среде внешние электрическое и магнитное поля способны создать объемную силу, вызывающую изменение веса жидкости. При этом электромагнитная сила не оказывает влияния на непроводящие включения. Квазиутяжеление металла электромагнитной силой приводит к выталкиванию неметаллических примесей на поверхность силами плавучести [6, 9 –11] . В дальнейшем всплывший шлак может быть механически удален с открытой поверхности металла вместе с оксидной пленкой. Для создания высокопроизводительного промышленного устройства, работающего на этом принципе, необходимо выбрать наилучшую конструкцию и методику воздействия электромагнитной силой. Но в первую очередь нужно решить задачу об аккумуляции примеси в определенной области расплава и способе ее изъятия.

Ключевой особенностью технологии электромагнитной сепарации является возможность создания необходимых электромагнитных сил в жидком металле бесконтактным способом, что позволяет использовать простые герметичные каналы, а также делает ненужным применение механических фильтров для отделения включений [6, 12] .

В лаборатории физической гидродинамики ФГУП ИМСС УрО РАН выполнен цикл работ по изучению процесса электромагнитной сепарации непроводящих включений в растворе щелочи, которые подтвердили работоспособность и эффективность методики и выявили некоторые особенности [13 –16] . Так, исследования показали, что критически важно учитывать в сепарационной ячейке топологию течения, которая обуславливается не только геометрией ячейки, но и способом приложения электромагнитной силы. Логичным продолжением этих работ стало рассмотрение процесса уже на жидком металле.

В качестве рабочей металлической среды выбран оловянно-свинцовый сплав ПОС-50, роль модельной примеси выполняют частицы меди. Для повышения технологичности процесса принято решение использовать переменное магнитное поле. Переменный ток пропускается по жидкому металлу, циркулирующему по контуру, содержащему насос, расходомер, сепарационную ячейку и перемешиватель (см. Рис .1) . В совокупности с ферромагнитными С-образными сердечниками, надетыми на канал, это позволяет генерировать объемные электромагнитные силы способные приводить металл в движение с помощью насоса, измерять его расход с помощью расходомера, и осуществлять процесс сепарации в ячейке (подробнее смотри в [17] ). На основании предыдущих исследований решено отыскивать оптимальную конструкцию (геометрию) сепарационной ячейки путем численного моделирования.

Итак, в работе численно исследуется гидродинамика в сепарационной ячейке при наличии перегородок различной конфигурации и при наличии/отсутствии внешней утяжеляющей электромагнитной силы. Целью является определение геометрии ячейки, обеспечивающей наилучшую сепарацию и накапливающую в себе частички примеси в процессе цикличного прокачивания через нее жидкого металла.

• 2.    Постановка задачи

Расчет выполняется в трехмерной постановке. Рассматривается ячейка длиной L = 480 мм и высотой H = h 1 + h ₂ = 180 мм (Рис .2, слева), заполненная жидким металлом. Толщина ячейки в перпендикулярном плоскости (x,y) направлении задается равной 12 мм. Рабочей средой служит жидкий металл — оловянно-свинцовый сплав; его свойства приведены в таблице. В середине ячейки расположена кассета, которую делят N непроницаемых перегородок с расстоянием между ними h =18 мм. Высота перегородок в расчете варьируется. В реальной МГД-установке такая кассета служит для аккумулирования частиц и извлекается в конце процесса сепарации.

В реальности на ячейку разомкнутой частью (ярмом), обращенной вниз, надеты ферромагнитные сердечники (см. Рис .1, позиция 6 ), которые при пропускании переменного тока через металл создают внешнюю утяжеляющую электромагнитную силу F в пространстве между ними (область, охватываемая сердечниками, обозначена

Рис. 1. Фотография оловянно-свинцового контура в сборе: 1 – бак, 2 – канал, 3 – трансформатор тока, 4 – кондукционный насос, 5 – кондукционный расходомер, 6 – сепарационная ячейка под слоем сердечников, 7 – электронагреватели, 8 – теплоизоляция

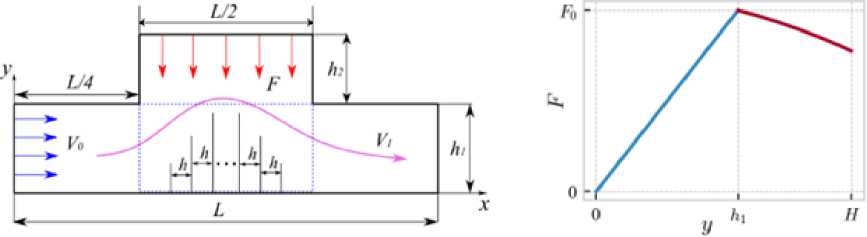
Рис. 2. Схема расчетной области (слева) и зависимость силы F от вертикальной координаты y (справа)

Таблица. Расчетные параметры

Параметры канала, [мм] Параметры рабочей среды Длина L 480 Высота H 180 Оловянно-свинцовый сплав Высота h1 100 Плотность 9000 кг/м3 Высота h2 80 Динамическая вязкость 0.0042 кг/м·с Глубина 12 Скорость на входе V0 5 мм/с на рисунке 2 слева пунктиром). Такая сила будет направлена в сторону ярма сердечника, то есть в данном случае вертикально вниз (см. Рис.2, слева). Генерация силы происходит следующим образом. Согласно [18], если на прямоугольный канал, по которому протекает переменный электрический ток, надеть С-образный ферромагнитный сердечник, то магнитное поле, создаваемое этим током, сформирует более интенсивное поле намагничивания. Полное магнитное поле B замкнуто в зазоре между сердечниками и проникает в канал преимущественно в перпендикулярном направлении. При этом на концах сердечника магнитное поле наибольшее, и оно почти линейно убывает к ярму.

В обсуждаемом случае массива сердечников возникающая электромагнитная сила

F=j X B (1)

является однородной по оси x в области их расположения. И хотя ток, протекающий по проводящей среде, является переменным, наводимая электромагнитная сила F является постоянной во времени, потому что результирующее магнитное поле B , входящее в формулу (1) , также меняет направление синфазно с током j (результат векторного произведения направления не меняет).

Электромагнитная сила по-разному действует на фазы среды, обладающие различной электропроводностью. Первая фаза — оловянно-свинцовый сплав, испытывает эффект квазиутяжеления, вторая фаза — примесь медных частиц, увлекается силой вертикально вниз в большей степени, чем первая фаза и улавливается перегородками, третья фаза — возможные непроводящие частицы (окислы, мусор), не испытывает воздействия и выталкивается вверх, на поверхность многофазной среды. За счет электромагнитной силы и осуществляется сепарация. Эта сила неоднородна вдоль осей x и y и задается из физических соображений: вблизи верхней границы сердечников (координата y = h 1 ) ей присваивается максимальное значение F 0 ; она ослабевает по линейному закону в области действия сердечников; за пределами сердечников сила убывает согласно квадратичному закону. По горизонтальной оси в областях x < L/4 и x> 3L/4 утяжеляющая сила считается нулевой. На рисунке 2, справа представлена зависимость силы F, действующей на жидкий металл, от вертикальной координаты y, заданная в расчете [17, 18] :

F = K •

ck 1 · y, y1,

[-k1 •у2 + k2, У ^ h1, где коэффициенты k1, k2 определяются из эксперимента и не меняются (в расчетах их величины взяты из статьи [18], где измерялись компоненты магнитной индукции, пропорциональной электромагнитной силе (1)), а коэффициент K при моделировании варьируется. Максимальное значение силы F0 принято равным 3600 Н, минимальное — 60 Н.

Сила F воздействует на поток жидкого металла, в результате чего топология течения меняется. Входящий в канал ячейки со скоростью V ₀ поток, имеющий плоский профиль, под действием электромагнитной силы F , а также с учетом геометрии канала (высоты перегородок) приобретает характерную топологию и скорость V(x,y). На выходе из канала выполняется условие отсутствия давления, то есть давление на выходе из канала равняется нулю.

Генерация магнитного поля потоком жидкого металла характеризуется магнитным числом Рейнольдса Re m = UL/n (U — характерная скорость, а п — коэффициент диффузии магнитного поля). В рассматриваемой задаче магнитное число Рейнольдса очень мало (Re m ~ 10 ^-3 — 10 -5 ), что позволяет пренебречь индуцированными полями и решать задачу в безындукционном приближении [19] .

Течение электропроводящей среды в рамках принятого безындукционного приближения описывается уравнениями:

^{d V} + ( V .V ) V = — ^V p +uA V + F , (3) ∂t ρ ρ

V- V = 0, (4)

где (3) — это уравнение Навье–Стокса, а (4) — уравнение неразрывности, в которых υ — вязкость, а ρ — плотность жидкого металла.

Достигаемые числом Рейнольдса Re = (V • h 1 )/(n/p) ~ 4.3 • 10 3 значения допускают возникновение турбулентных течений (за характерный размер выбрана высота ячейки h 1 ). Однако в рамках поставленной задачи интерес представляют средние установившиеся течения, в которых мелкомасштабные возмущения сглажены и усреднены. Проведен отдельный расчет с применением LES-модели турбулентности. Полученное стационарное течение оказалось идентичным представленному далее в статье (без использования модели турбулентности). В связи с этим принято решение не включать турбулентность в расчеты.

Вычисления осуществлялись в программном комплексе ANSYS Fluent. Расчетная область состояла из 315226 конечных элементов и содержала 486325 узлов. Проведена оценка сеточной сходимости, в результате выбран шаг сетки, равный 2 мм. При дальнейшем уменьшении шага по координате значительно возрастало время расчета, но не увеличивалась точность получаемого решения. Шаг по времени составлял 0.05 с, число Куранта не превышало 0.1. Таким образом, выполнено необходимое условие устойчивости численного решения. Критерием остановки расчетов служило фиксированное число временных шагов. За приблизительно половину этого времени течение точно выходило на статистически постоянное состояние.

• 3.    Результаты

• 3.1.    Вариация высоты перегородок без утяжеляющей силы

Выполнено численное моделирование гидродинамики в сепарационной ячейке. Геометрические параметры ячейки и физические параметры среды [20, 21] представлены выше в таблице.

Проведены расчеты при различной высоте перегородок: от 30 до 90 мм с шагом 20 мм, при отсутствии внешней силы; получены поля модуля скорости в плоскости (x,y) для различных моментов времени вплоть до достижения установившегося режима (Рис. 3). Выход на установившийся режим произошел за 17 с реального времени. Для получения общей картины гидродинамики течения в ячейке сначала рассматривались только две перегородки: на входе и на выходе сепарационной ячейки.

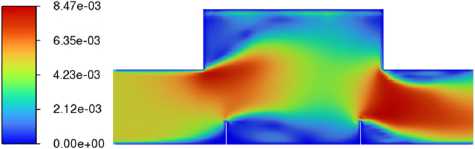
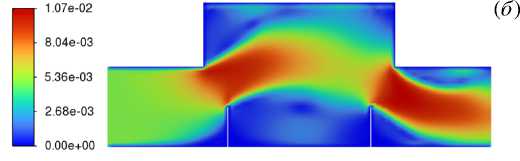
( г )

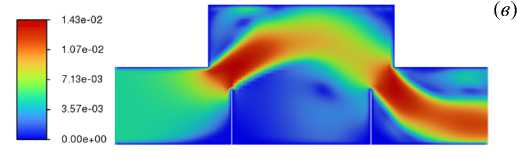
Рис. 3. Установившееся поле модуля скорости | V | , [м/с] в плоскости (x,y) для четырех значений высоты перегородок, [мм]: 30 ( а ), 50 ( б ), 70 ( в ), 90 ( г )

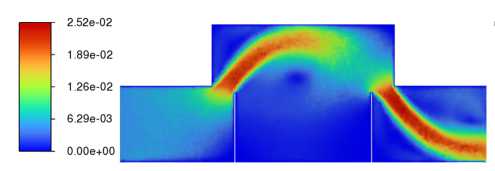
Из полученных распределений видно, что перегородки любой высоты создают сужение канала, что вызывает локальный рост скорости потока в соответствующих зонах (пропорционально величине сужения канала) и ведет к образованию струи. Для высоты перегородок 30 мм скорость в струе возрастает в 1.5 раза. Струя занимает практически всю площадь ячейки, и вихри не образуются. При высоте перегородок 50 мм скорость в струе увеличивается в 2 раза, струя по-прежнему остается широкой, и возникает два возвратных вихря: один в верхней части ячейки, другой в области между перегородками. При высоте перегородок 70 мм скорость в струе становится больше уже в 3 раза, струя превращается в достаточно узкую и локализованную, возвратные вихри также локализуются. При высоте перегородок 90 мм скорость в струе возрастает в 5 раз, струя остается узкой и сопровождается образованием одного большого вихря в зоне расположения удерживающих перегородок.

Для эффективного процесса сепарации скорость транзитного течения должна быть небольшой, с другой стороны, область удержания примеси должна обладать большой площадью для накопления частиц. Исходя из этих требований оптимальной высотой перегородок выбрано 70 мм. При такой высоте с добавлением числа перегородок паразитный возвратный вихрь в нижней части ячейки образовываться не будет.

• 3.2.    Вариация величины утяжеляющей силы при фиксированной высоте перегородок

  В реальной экспериментальной МГД-установке электромагнитная сепарирующая сила создается при помощи ферромагнитных сердечников, надетых на ячейку снизу. При протекании тока вдоль ячейки возникает магнитное поле вокруг канала и концентрируется ферромагнитными сердечниками. При взаимодействии тока и сконцентрированного магнитного поля образуется сила, направленная вертикально вниз, в область наименьшего поля. На следующем этапе проведено численное моделирование гидродинамики в сепарационной ячейке с перегородками выбранной высоты (70 мм) при наличии внешней утяжеляющей силы F, и вариациях коэффициента K (см. формулу (2) ) в диапазоне от 10 до 60 с шагом 10 (Рис. 4) . Сила F 0 , соответствующая этим значениям K, изменялась от 60 до 3600 Н.

Внешняя утяжеляющая электромагнитная сила создает избыточное давление в нижней части ячейки и отжимает поток в верхнюю часть. Также добавление силы приводит в верхней правой части ячейки к образованию дополнительного вихря, интенсивность которого растет с увеличением силы. Для эффективного процесса сепарации сила должна быть наибольшей. С другой стороны, число и интенсивность побочных вихрей должны быть наименьшими. Кроме этого, необходимо, чтобы струя проходила непосредственно над перегородками, тогда электромагнитная сила, действующая на частицы с проводимостью большей, чем у жидкой среды, будет увлекать их вниз, в область между перегородками (подобно тому, как это происходит в обычных магнитных сепараторах [22] ). Таким образом, пороговому значению силы соответствует K =30, а оптимальному — K=20.

Следует упомянуть, что неизбежно возникающий при наложении внешней силы интенсивный вихрь в верхней правой части может быть полезен для аккумуляции частиц, обладающих проводимостью меньшей, чем у жидкой проводящей среды. Большая часть этих частиц попадет в зоны между перегородками и при извлечении кассеты

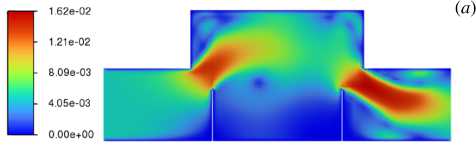
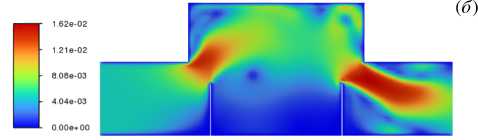
Рис. 4. Установившееся поле модуля скорости | V | , [м/с] в плоскости (x,y ) для шести значений внешней силы, отвечающей значениям коэффициента K: 10 ( а ), 20 ( б ), 30 ( в ), 40 ( г ), 50 ( д ), 60 ( е )

удалится из потока.

• 3.3.    Моделирование конструкции кассеты и вариация начальной скорости потока

На заключительном этапе проведено численное моделирование гидродинамики в сепарационной ячейке с выбранной оптимальной высотой перегородок и значением внешней силы. Первая и последняя перегородки имели высоту 70 мм. Перегородки между ними располагались с шагом h = 18 мм, а их высота сначала возрастала (до середины ячейки по горизонтали), а затем убывала вслед за формой струи. Такая конфигурация проверялась вычислениями устойчивости течения при вариации входной скорости потока от 5 до 15 мм/с с шагом 5 мм/с (Рис. 5) .

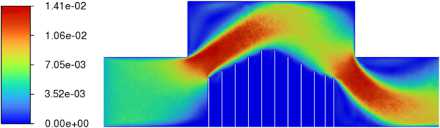
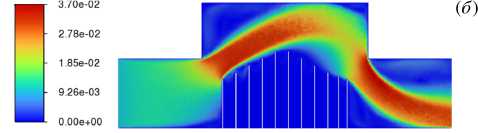
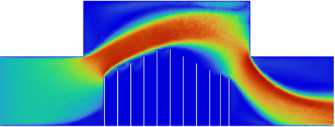
Рис. 5. Установившееся поле модуля скорости | V | , [м/с] в плоскости (x,y ) для трех значений входной скорости потока, [мм/с]: 5 ( а ), 10( б ), 15 ( в )

Во всех случаях струя устанавливается в пространстве таким образом, что следует «по верхам» перегородок, причем по мере увеличения скорости прижимается к ним все ближе. Также с ростом скорости потока пропадает побочный вихрь в верхней правой части ячейки. В зонах между перегородками не возникает паразитных вихрей, которые потенциально могли бы способствовать вымыванию примеси из этого пространства.

• 4.    Заключение

Проведенное моделирование течения жидкого металла в сепарационной ячейке под воздействием внешней утяжеляющей силы позволило определить оптимальные геометрические параметры кассеты для продуктивной аккумуляции примеси, а также величину действующей силы. Получено, что наибольший сепарационный эффект может быть достигнут при совокупности следующих параметров: высоты стенок в кассете 70 мм, интенсивности силового воздействия с коэффициентом K = 30, а также начальной скорости потока V 0 = 5 мм/с.

Показано, что в некоторых режимах возникают интенсивные паразитные вихри (см., например, Рис. 4 при K > 30), которые могут значительно снизить качество процесса сепарации. Вариация скорости на входе в ячейку не приводит к существенному изменению топологии течения. Это означает, что небольшое изменение скорости циркуляции рабочей среды в контуре реальной МГД-установки не приведет к нарушению процесса сепарации.

В результате вычислительных экспериментов выбрана оптимальная конфигурация сепарационной ячейки, соответствующая режиму с наиболее эффективной сепарацией, по четырем параметрам: высоте перегородок, величине внешней утяжеляющей электромагнитной силы, скорости потока и топологии промежуточных перегородок.

Исследование выполнено за счет гранта Российского научного фонда и Пермского края № 22-19-20106,