Моделирование кинематики пластического течения при калибровке тонкостенной прецизионной трубы обжатием

Элементы трубопровода летательных аппаратов из титановых сплавов и коррозионностойких сталей подлежат калибровке перед сборкой в трассу трубопровода. Калибровка применяется для подготовки стыкуемых кромок с целью устранения несоответствия диаметров и овальности. При этом отклонения наружного диаметра калиброванного конца тонкостенных прецизионных труб под автоматическую сварку кольцевых стыков не должны превышать ± 0,15 мм от номинального размера [1].

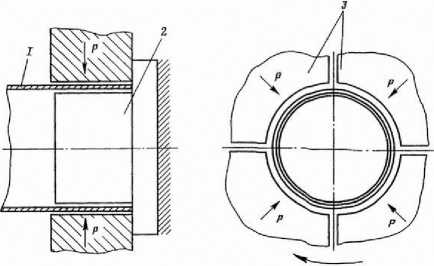
Сущность известного способа калибровки заключается в обжатии трубы многосекторной матрицей[2] (рисунок 1). Рабочее движение секторов матриц - радиальное по направлению к оси трубы.

м

Рисунок 1. Схема калибровки многосекторной матрицей:1 – труба калибруемая; 2 – оправка; 3 – секторы матрицы

В теоретическом плане процесс калибровки труб способом обжатя многосекторным инструментом активно изучается отечественными и зарубежными учеными. Так, в работе [3] произведен расчет силовых параметров при ротационном обжиме тонкостенных труб. Экспериментальное исследование устойчивости заготовки при обжиме проводилось в [4] на трубах из стали ШХ-15 с различными геометрическими параметрами. Поскольку устойчивость трубных заготовок зависит от соотношения их геометрических параметров, штамповой оснастки, условий интенсификации процесса обжима, то варьируемыми параметрами в опытах выбрана высота и толщина стенки трубы.

В то же время причины раннего гофро-образования (рисунок 2) при калибровке обжатием особотонкостенных труб многосекторным инструментом изучены недостаточно. В открытой печати отсутствуют сведения о продольной устойчивости тонкостенной прецизионной трубы в результате обжима ее концов многосекторным инструментом в процессе калибровки перед автоматической сваркой кольцевых стыков. Не выявлено влияние относительной толщины стенки трубы, ее диамет- ра, величины обжатия, количества секторов разжимного инструмента и механических характеристик используемых сплавов на потерю устойчивости в продольном направлении.

Рисунок 2. Потеря устойчивости стенкой трубы при калибровке обжатием

Оценка устойчивости деформирования с использованием энергетического критерия устойчивости выполняется по результатам сопоставления энергетических (силовых) параметров для основного (устойчивого) и возмущенного состояний. Поэтому для решения задачи об устойчивости процесса деформирования необходимо иметь модель кинематики течения и энергосиловые параметры для основного состояния.

Для моделирования кинематики течения при обжатии трубы и определения необходимого давления обжатия используем метод верхней оценки. Согласно этому методу, любое кинематически возможное поле скоростей позволяет получить верхнюю оценку усилия деформирования. Для действительного поля скоростей верхняя оценка усилия достигает минимального (точного) значения. Схема калибровки обжатием края трубы и геометрические параметры процесса представлены на рисунке 3.

Для описания геометрии заготовки используем цилиндрическую системукоординат r , θ , z . Границы изменения координат для деформируемой части заготовки определяются неравенствами:

R - t ≤ r ≤ R ;  0 ≤ θ≤ 2 π ; 0 ≤ z ≤ l (1)

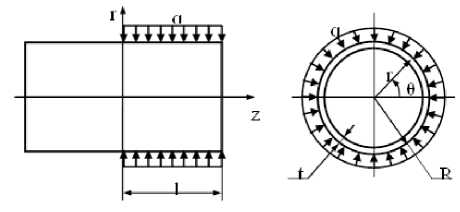
Рисунок 3. Схема и геометрические параметры калибровки

Поле скоростей, описывающее пластическое течение заготовки должно удовлетворять условию несжимаемости и кинематическим краевым условиям. Калибровка представляет собой осесимметричный процесс. Поэтому примем, что окружная компонента v ₉ вектора скорости равна нулю.

Условие несжимаемости в указанной системе координат с учетом принятого допущения имеет вид:

+ Vr. ₊     - 0 ,            (2)

dr   r   dz а компоненты тензора скоростей деформаций определяются по формулам:

εr

d v_r d r

Принимаем, что радиальная компонента скорости определяется выражением:

vr = -rz .

При этом будет выполнено одно из условий (4).

Подставляя (5) в (2), находим:

Vz = z2 + f1(r) , где f (r)- неизвестная функция.

Функцию f ₁ (r) найдем из условия выполнения соотношений (4) и (1):

f1 (r) --12.(7)

Подставляя (7) в (6), окончательно будем иметь:

Vz = z2 -12.(8)

Поле скоростей, в этом случае, описывается уравнениями вида:

γzr

9v,   dvr

—z. + —r dr 9z

vr

- rz

Так как характер течения металла неизвестен, то рассмотрим несколько вариантов полей скоростей и для каждого из них определим необходимую величину давления обжатия. Наилучшим будет являться тот вариант, для которого величина давления имеет наименьшее значение. Допустимыми являются не только непрерывные, но и разрывные поля скоростей.

Рассмотрим следующие варианты деформирования заготовки:

• -    вариант№ 1- непрерывное поле скоростей, при котором уменьшение наружного радиуса R происходит при увеличении длины l калибруемой части трубы;

• -    вариант № 2- непрерывное поле скоростей, при котором уменьшение наружного радиуса R происходит только за счет увеличения толщины стенки трубы t ;

• - вариант №3- разрывное поле скоростей, при котором уменьшение наружного радиуса R происходит только за счет увеличения толщины стенки трубы t . В этом случае имеет место разрыв в радиальной компоненте скорости на границе между калибруемым участком и основной трубой.

Из системы уравнений (3) определяем компоненты тензора скоростей деформаций:

^er-^-z_z ^e 6 =^{- z}

8 z = ² Z . Y zr = ^{- r}

Мощность пластической деформации определяется по формуле:

N пл - k J HdV , V

где V – объем пластической области; k – предел текучести при сдвиге, осредненный по объему пластической области; H – интенсивность скоростей деформаций сдвига.

При принятых допущениях интенсивность скоростей деформаций сдвига равна:

H ^- V^{2 (} S ² +S 9 ^{+s 2 )} + Y 2 r .           ⁽¹²⁾

Используя (10), (11) и (12), находим:

Вариант № 1.

Кинематические краевые условия для данного варианта имеют вид:

V r l z = 0 = ⁰ ■   V z|z - l = ⁰ .                    (4)

lR

N_пл - 2 n k J J V12 z ² + r ² rdrdz .        (13)

0 R -1

Для тонкостенных труб - <<  R . Поэтому при вычислении интеграла (13) можно принять r = R . С учетом этого упрощения выражение (13) принимает вид:

N пл = 2 п k j V12 z ² + R ² dz .            (14)

Применяя изложенную для варианта № 1 методику по определению мощности пластической деформации и мощности внешнего давления и используя уравнение баланса мощностей (18), получим формулу для определения относительного давления обжатия q :

Используя для вычисления интеграла (14) неравенство Коши-Буняковского, находим:

2 t

l

4 l ²

1 +--- т"

3 R ²

N„ = 2 n kR-l V4 l ² + R ² .              (15)

Мощность давления обжатия при калибровке определяется по формуле:

N q = q j v _r| _r _ R dS ,               (16)

S где S – площадь наружной поверхности трубы, нагруженной давлением q.

Вычисляя с использованием соотношений (9) интеграл (16), получим:

Nq = qnR2l2.(17)

Для определения давления обжатия q используем уравнение баланса мощностей:

Nq = N пл.(18)

Из соотношений (18), (14) и (1 7) находим:

q о = - 1 + 4 — ,(19)

lR где q0 = q - относительное значение давления 0k обжатия.

Вариант № 2.

Кинематические краевые условия для варианта 2 имеют вид (4). Принимаем для радиальной компоненты скорости выражение:

vr

z

r

Подставляя (20) в (2), находим:

V z = 0.                          (21)

Сопоставляя (19) и (23) приходим к выводу, что при любом сочетании геометрических параметров давление для варианта № 2 меньше давления для варианта № 1. Это означает, что кинематика варианта № 2 лучше описывает течение металла при калибровке обжатием по сравнению с вариантом № 1.

Вариант № 3.

В варианте 3 рассмотрим поле скоростей, при котором имеет место разрыв радиальной компоненты скорости на границе между калибруемым участком и основной трубой. В этом случае при моделировании кинематики первое из соотношений (4) не используется.

Принимаем, что радиальная компонента скорости определяется выражением:

v_r =- ¹.                     (24)

r

Подставляя (24) в (2), получаем:

V z = 0.                          (25)

Для принятых соотношений (24) и (25) условия (4) выполняются.

Поле скоростей для варианта № 3 имеет вид:

1 v r =~~r

< v e = ⁰    .                  ⁽²⁶⁾

v z = ⁰

Используя соотношения (26) и (11) находим, что мощность пластической деформации при условии - <<  R равна:

Для полученных выражений (20) и (21) условия (4) выполняются.

Поле скоростей для варианта № 2 имеет вид:

N _л= 4 n kl- . пл

R

vr

z

r

• ^ve = 0

v z = ⁰

Мощность диссипации энергии на поверхности разрыва скоростей определяется по формуле:

D = j k [ v "dS ,                   (28)

Sp где Sp - площадь поверхности разрыва скоростей; [v] - величина разрыва скорости.

Величина разрыва скорости на поверхности между калибруемым участком и основной трубой равна:

[ ► ] = ¹. r

Подставляя (28) в (27), находим:

D = 2 n kt .                    (30)

По соотношениям (16) и (25) определяем мощность внешнего давления:

N_q = 2 q n l .                   (31)

Уравнение баланса мощностей в данном случае имеет вид:

Используя (27), (30),(31)и (32), находим, что относительное давление обжатия q равно:

q о = -( 1 + 2 b) . (33) lR

Из сопоставления зависимостей (23) и (33) следует, что при любой относительной длине калибруемого участка трубы q I >  q I¹ , где q 0I , q 0II - относительные давления обжатия для вариантов № 2 и № 3 соответственно.

На рисунке 4 представлены графические зависимости изменения относительного давления обжатия q .

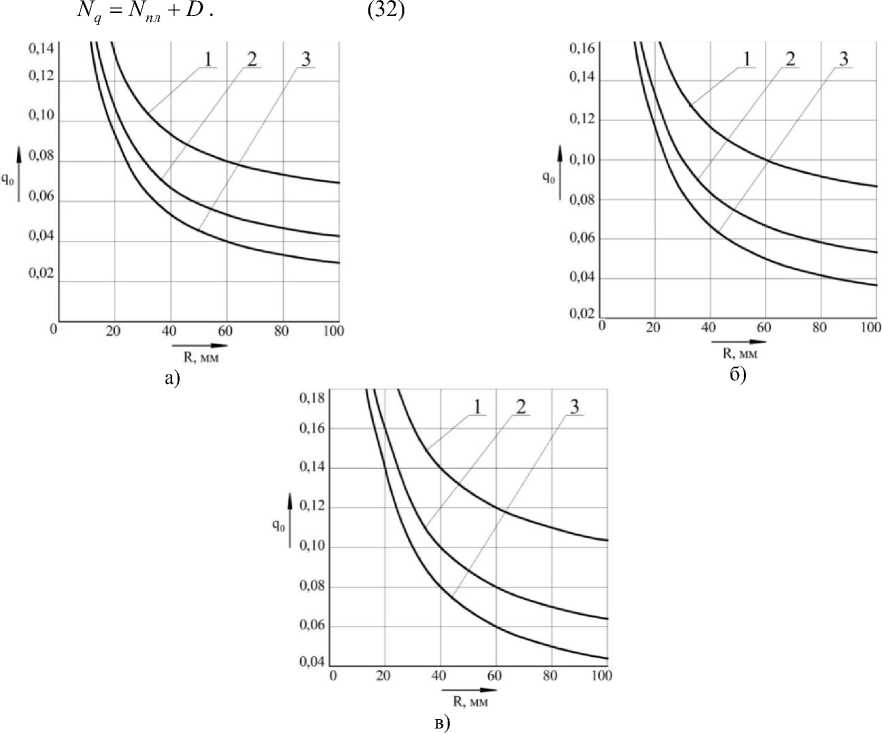
Рисунок 4 Зависимости между радиусом R калибруемой тонкостенной трубы и относительным давлением обжатия q ₀: а – при t =0,8 мм; б – при t =1,0 мм; в – при t =1,2 мм: при длине калибруемого участка трубы: 1 – l =15 мм, 2 – l =30 мм, 3 – l =60 мм

Можно сделать следующие выводы:

• 1.    При описании пластического течения и определении энергосиловых параметров при калибровке трубы обжатием рекомендуется использовать кинематику по варианту № 3.

• 2.    С увеличением шага подачи l при калибровке многосекторным инструментом требуемое давление обжатия q уменьшается (рисунок 4).

• 3.    При одинаковом шаге подачи l трубу с меньшей относительной толщиной t/R необходимо калибровать меньшим давлением обжатия (рисунок 4).

• 4.    С возрастанием предела текучести при сдвиге материала трубной заготовки давление обжатия q ₀ увеличивается.

Вестник ВГУИТ, №4, 2014