Моделирование конструкции ошпаривателя для термохимической обработки свекловичной стружки перед экстрагированием сахарозы

Технология свеклосахарного производства представляет собой совокупность сложнейших тепло- и массообменных процессов, одним из которых является экстрагирование сахарозы из клеток свекловичной ткани. Для осуществления экстрагирования свекловичную ткань необходимо предварительно прогреть до температуры, Для цитирования

обеспечивающей денатурацию белков [1–3]. Этот процесс существенно ускоряется при комплексном тепловом, электрическом и химическом воздействии [4–9]. Предложена конструкция ошпаривателя для термохимической обработки свекловичной массы, уточнение параметров которой осуществляли с использованием методов математического моделирования [10–13].

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

Процесс термохимической обработки свекловичной стружки в ошпаривателе является достаточно сложным с точки зрения описания. В математической модели необходимо максимально адекватно представить отдельные элементы свекловичной стружки, их способность к изгибу, движение в пространстве, взаимодействие между собой, с каплями реагента и с рабочими поверхностями ошпаривателя.

Многие модели аналогичных процессов используют приближения постоянства геометрических параметров обрабатываемого объекта или грубые приближения сплошной среды. Однако указанные приближения при описании термохимической обработки свекловичной стружки существенно снижали бы адекватность модели. Поэтому в настоящей работе была поставлена задача разработки математической модели термохимической обработки свекловичной стружки с высокой детализацией и адекватностью на основе вычислительных возможностей современных компьютеров.

Материалы и методы

В работе применили конечно-элементный подход путем представления сложных тел в виде большого количества отдельных однотипных элементов. При этом каждый элемент свекловичной стружки разбивали на шарообразные частицы диаметром d Э 0,5 см (рисунок 1). Для моделирования использовали метод динамики частиц.

При моделировании процесса введен ряд коэффициентов, связанных с дискретизацией стружки (разбиением на отдельные шарообразные элементы): m Э , c С , d ЭС , c ИС . Их расчет осуществляли по справочным данным и специально проведенным калибровочным экспериментам.

Расчет массы одного элемента стружки m Э проводили с использованием значения плотности сахарной свеклы и простых геометрических соображений:

πd mЭ=ρ⋅ 4С dЭ, (1)

где ρ – характерная плотность корнеплода сахарной свеклы; d С – эффективный диаметр свекловичной стружки.

Для расчета коэффициента жесткости взаимодействия двух элементов c с провели испытания на сжатие образцов свеклы исходной и обработанной растворами сульфатов алюминия и аммония (рисунок 2). Обнаружено, что образцы размерами 40x40x50 мм³ сжимаются в вертикальном направлении с 50 до 40 мм при приложении давления около 2,5 МПа. Тогда коэффициент жесткости можно рассчитать по формуле

P с = Hd , (2) С∆H Э, где P – давление при испытании на изгиб; H – высота образца; ΔH – изменение высоты образца в процессе испытаний [14].

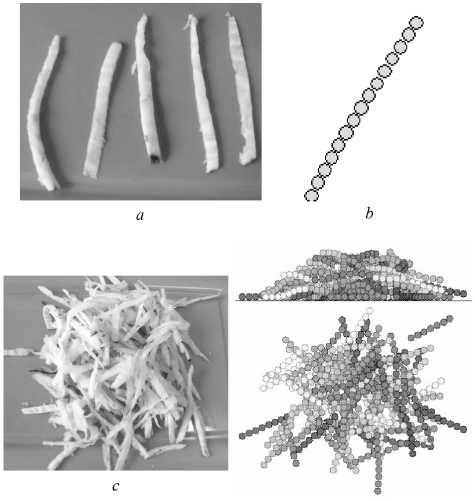
d

Рисунок 1. Представление свекловичной стружки в процессе моделирования: a, c - фото реальной стружки; b, d – представление в модели

Figure 1.Representation of beet chips in the modeling process: a, c – photo of real chips; b, d – representation in the model

Рисунок 2. Испытание на сжатие образца свеклы, обработанного раствором сульфата аммония

Figure 2. Compression test of a beet sample treated with ammonium sulfate solution

Подставляя значения переменных в последнюю формулу, получаем c с = 6,5 · 10⁴ Н/м.

Расстояние обнуления взаимодействия между соседними элементами стружки d О рассчитывали через предел прочности на растяжение для корнеплода сахарной свеклы, определяемый в механических испытаниях образца. Экспериментально получено значение d О 0,07 d Э .

Для расчета коэффициента изгибной жесткости c ИС1 , приведенного к тройке соседствующих элементов, проведены испытания стружки на изгиб по схеме, представленной на рисунке 3. Испытания проводили в горизонтальной плоскости, чтобы исключить влияние на результаты силы тяжести.

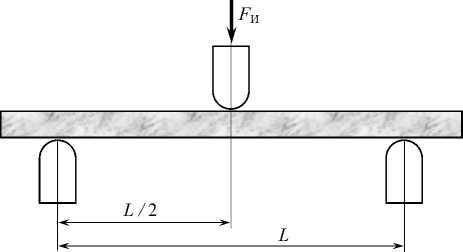
Рисунок 3. Схема испытания свекловичной стружки на изгиб для определения коэффициента изгибной жесткости c ИС

Figure 3. Scheme of beet chip bending test to determine the coefficient of bending stiffness c ИС

При данной схеме испытаний оценочное значение коэффициента cИС1 можно рассчитать по формуле сИС 1

F d

ИЭ ---—.

А Н ( L /2 )2 ’

где F И – сила, необходимая для изгиба стружки; Δ H – величина прогиба стружки под действием силы; L – расстояние между упорами, на которых расположена стружка. Измерения показали, что при длине L = 50 мм и величине изгибающей силы 0,1 Н величина прогиба в центре составляет Δ H = 6–10 мм. Тогда, приняв для определенности Δ H = 8 мм, в расчете по формуле получили с ИС1 = 100 Н/м и использовали это значение при дальнейшем моделировании.

При описании взаимодействия рабочих поверхностей ошпаривателя (форсунки и центральной трубы) (рисунок 4) с отдельными элементами стружки использовали упруговязкие характеристики для расчета силы взаимодействия F ^ЭП. Для расчета силы упругого взаимодействия между i -м элементом стружки и поверхностью необходимо определить величину внедрения r внi элемента в поверхность ошпаривателя, а также определить вектор { n хi , n уi , n zi } к поверхности в точке внедрения. Далее упругая сила вычисляется по закону Гука с коэффициентом жесткости 2× с с , при этом направление силы, действующей на элемент, считается вдоль нормального вектора. Декартовы составляющие силы вязкого трения пропорциональны составляющим абсолютной скорости элемента vxi, vyi, vzi с коэффициентом вязкого трения k в .

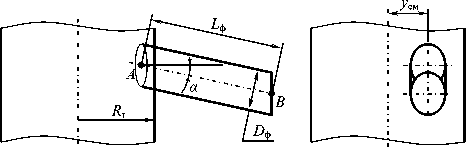
Рисунок 4. Геометрические параметры форсунки и центральной трубы

Figure 4. Geometric parameters of the nozzle and the central pipe

Результаты и обсуждение

Предлагаемая математическая модель реализована в виде системы большого числа дифференциальных и алгебраических уравнений. Для удобства исследования системы разработана компьютерная программа на языке Object Pascal в интегрированной среде программирования Borland Delphi 7.0, предназначенная для проведения компьютерных экспериментов по взаимодействию потока свекловичной стружки с поверхностями ошпаривателя.

В начальный момент времени свекловичная стружка в количестве 100 элементов распределяется случайным образом выше исследуемой области вблизи форсунки. Координата центра стружки, угол наклона стружки в вертикальной плоскости, угол ориентации стружки в горизонтальной плоскости определяются с помощью генератора случайных чисел, реализующего равномерный закон распределения. Начальные скорости движения элементов стружки равны нулю: v ⁰ = 0, v0_f = 0 , v 0i = 0 .

Перемещение элементов ограничено границами модельного пространства. На расстоянии 1 м под исследуемой областью вблизи форсунки находится горизонтальная поверхность, ограничивающая движение стружки. Стружка постепенно накапливается на поверхности (рисунок 1, d ). Взаимодействие стружки в модели принимается упруго-вязким и описывается дополнительными слагаемыми в уравнениях.

Также движение элементов ограничивают поверхности форсунки и центральной трубы.

В процессе компьютерного эксперимента имитируется вертикальное движение потока свекловичной стружки сечением 8x8 см. До исследуемой области пространства свекловичная стружка движется вниз с постоянной скоростью 0,2 м/с, непосредственно над исследуемой областью пространства скорость стружки не ограничивается, она начинает двигаться с ускорением свободного падения. В исследуемой области пространства поток свекловичной стружки взаимодействует с форсункой и центральной трубой.

Разработанная модель позволяет варьировать большое количество конструктивных и технологических параметров ошпаривателя и механико-геометрических параметров свекловичной стружки. В ходе компьютерного эксперимента модель позволяет определять большое количество показателей, характеризующих эффективность термохимической обработки стружки: производительность, качество, экономичность. Для дальнейшего теоретического исследования выбраны только наиболее важные входные и выходные параметры (рисунок 5).

Конструктивные и технологические параметры

Design and technological parameters

α L ф

D ф

Модель взаимодействия стружки с форсунками Model of interaction of chips with nozzles

m н t к

Показатели эффективности

Performance indicators

Рисунок 5. Входные параметры и выходные характеристики математической модели

Figure 5. Input parameters and output characteristics of the mathematical model

В качестве конструктивных параметров выбраны: α – угол наклона форсунки в вертикальной плоскости; L ф – длина форсунки; D ф – диаметр форсунки.

Эффективность ошпаривателя характеризуется следующими показателями: m н – масса свекловичной стружки, накопившейся на форсунке (средняя в течение компьютерного эксперимента); t к – время контакта свекловичной стружки с поверхностями ошпаривателя – форсунками и центральной трубой (среднее в течение компьютерного эксперимента).

Расчет показателей эффективности производили по следующим формулам.

A t I К Д¹ t 1     N a J ^1, z ур i <  z i <  z ур 2 ;

m„ = / m ^ / ^

K t!     ы [ 0, z i <  z ур i или z i >  z yp 2 ;

1 N a ^{[ t}K3 / ^{A 1} ]

t :

к   N₃ 1/ ^

At, если элемент i контактирует с форсункой;

0, если не контактирует;

где Δ t – шаг интегрирования дифференциальных уравнений; t КЭ – длительность компьютерного эксперимента; τ – номер шага интегрирования; z ур1 и z ур2 – уровни ниже и выше форсунки, в пределах которых стружка считается накопившейся на форсунке; N Э – количество элементов стружки; d Э – диаметр элементов стружки.

Накопление свекловичной стружки на форсунках и ее перегрев существенно зависят от геометрических параметров форсунки: угла наклона α , длины L ф и диаметра D ф . Поэтому было исследовано влияние данных параметров на накапливающуюся на форсунке массу m н и среднее время контакта стружки с поверхностью форсунки t к .

Наклон форсунок на 10о позволяет вдвое уменьшить массу накапливающейся на форсунках стружки и в 3,5 раза уменьшить время контакта стружки с форсунками. При угле наклона более 25о стружка практически не накапливается на форсунках, а время контакта стружки с форсункой не превышает 0,06 с (рисунок 6).

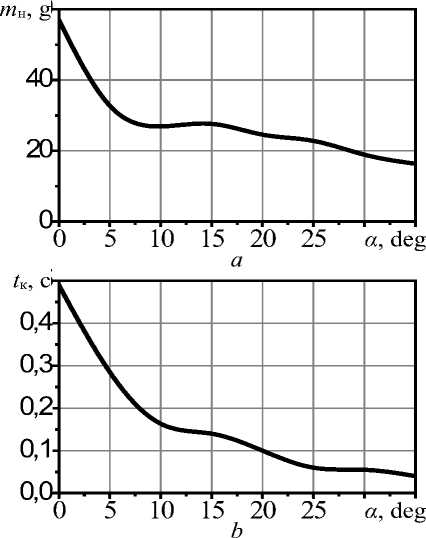
Рисунок 6. Графическая интерпретация зависимости массы накапливающейся на трубке стружки m н (a) и среднего времени контакта стружки с трубкой t к (b) от угла наклона форсунки α

Figure 6. Graphical interpretation of the dependence of the mass of chips accumulating on the tube m н (a) and the average time of contact of the chips with the tube t к (b) on the angle of inclination of the nozzle α

Независимо от длины форсунок наклон на 20о позволяет в 1,4–2,1 раза снизить массу накапливающейся стружки и в 2,7–8,0 раз уменьшить время контакта стружки с форсункой (рисунок 7).

При увеличении диаметра форсунки влияние угла наклона проявляется значительнее: диаметр до 1 см при наклоне форсунки на 20о уменьшает накопление массы в 1,5 раза, время контакта в 3 раза; при диаметре 2–3 см тот же угол наклона снижает накопление стружки на поверхности форсунки в 3 раза, время контакта в 5–8 раз (рисунок 8).

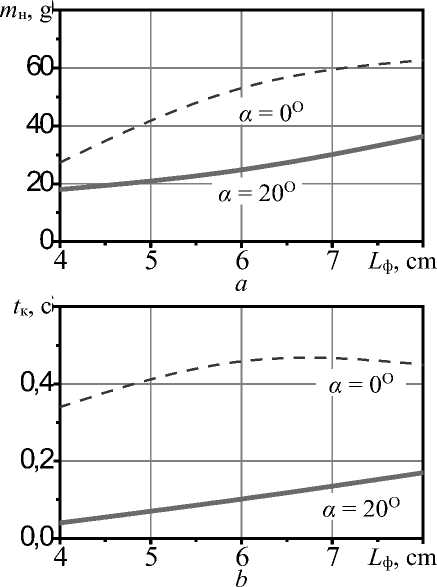
Рисунок 7. Зависимость массы накапливающейся на форсунке стружки m н (a) и среднего времени контакта стружки с трубкой t к (b) от длины форсунки L ф

Figure 7. Dependence of the mass of chips accumulating on the nozzle m н (a) and the average time of contact of the chips with the tube t к (b) on the length of the nozzle L ф

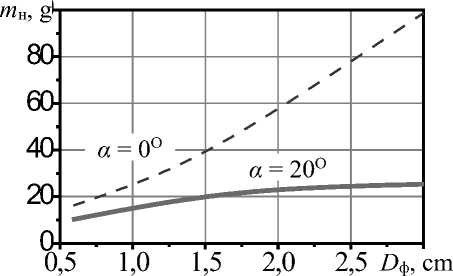
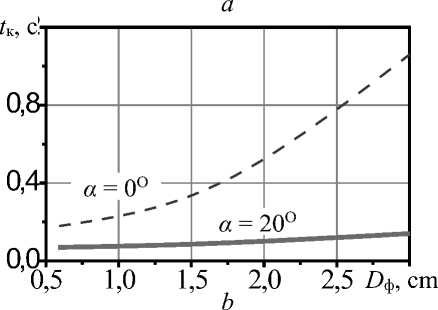
Рисунок 8. Влияние диаметра форсунки D ф на массу накапливающейся на трубке стружки m н ( а ) и среднее время контакта стружки с форсункой t к (b) Figure 8. Influence of the nozzle diameter D ф on the mass of chips accumulating on the tube m н ( а ) and the average contact time of the chips with the nozzle t к (b)

Заключение

Проведены оценочные испытания образцов свеклы исходной и обработанной жидкостью для электрохимической активации (растворами сульфатов алюминия и аммония) на сжатие, растяжение и изгиб для определения коэффициентов модели.

Разработана программа для ЭВМ, реализующая модель, и позволяющая исследовать влияние геометрических параметров форсунок на показатели накопления стружки на форсунках.

Математическая модель взаимодействия свекловичной стружки с внутренней поверхностью ошпаривателя позволяет определить массу стружки, накапливающейся на форсунках, и среднее время контакта стружки с форсунками. Проведенные исследования предназначены для выбора конструкционных характеристик опытных образцов ошпаривателя [15].