Моделирование наноканалов в синтезированных мембранах
Автор: Алексеев М.С., Пономарв Р.Р., Шелистов В.С., Попов В.А., Моршнева И.В., Демхин Е.А.
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 1 т.17, 2024 года.
Бесплатный доступ
Численно исследуется поведение разбавленного электролита в системе из состыкованных микроканала и наноканала с заряженными непроводящими стенками под действием внешних разности потенциалов и давления. Наличие на~стенках наноканала поверхностного заряда препятствует прохождению через него ионов соответствующего знака. Вследствие этого рассматриваемая система приобретает ионоселективные свойства и с некоторыми допущениями может рассматриваться как фрагмент ионообменной мембраны, в том числе синтезированной путём создания нанопор в диэлектрическом материале. Подобные системы используются в экспериментах по управлению движением заряженных частиц за счёт концентрационной поляризации. Целью работы является изучение влияния отдельной поры на течение электролита и возможности управления этим течением путём изменения геометрических и физических свойств поры. Инструментом исследования являются специально разработанные упрощённые модели, основанные на усреднении по поперечному сечению уравнений Нернста~Планка, Пуассона и Стокса и сведении их к единственному нелинейному дифференциальному уравнению. Упрощённые модели позволяют вычленить вклад физических механизмов движения электролита ~ напорного (порождаемого внешним механическим воздействием) и электроосмотического (порождаемого электрическим полем). Для численного решения уравнений применяется конечно-разностный метод с полунеявным интегрированием по времени. Выявлено, что поведение системы качественно совпадает с поведением ячейки ионообменной мембраны, обладающей неидеальной селективностью; в частности, модель правильно предсказывает наличие допредельного и предельного токовых режимов, а также вихреобразование у входа в наноканал вследствие конкурирования механизмов движения электролита. Предложенные модели допускают обобщение на канал любой геометрии и на электролит с произвольным числом ионов.
Мембрана, наноканал, система нернста-планка-пуассона-навье-стокса, электроосмос, численное моделирование
Короткий адрес: https://sciup.org/143182743
IDR: 143182743 | УДК: 537.36, | DOI: 10.7242/1999-6691/2024.17.1.1
Текст научной статьи Моделирование наноканалов в синтезированных мембранах
Статья опубликована в открытом доступе по лицензии CC BY 4.0
Течение электролита в мембранах обычно описывается уравнениями Пуассона и Дарси [9 –11] . В достаточно широких каналах используется подход, основанный на предположении об электронейтральности электролита вне тонких (до 100 нм) дебаевских слоёв [12] . Для наноканалов, о которых говорилось выше, это предположение может нарушаться, в результате чего возникает необходимость в решении полной нелинейной системы уравнений Нернста– Планка, Пуассона и Навье–Стокса [13] , которая при нетривиальной геометрии канала сложна с вычислительной точки зрения. Задача течения в наноканалах решалась численно в полной постановке в работах [14, 15] , где найдены «концентрационные скачки», напоминающие ударные волны газовой динамики. Полученный результат имеет и фундаментальное значение (особенно для механиков, как проявление типичной черты нелинейности), и практическое (в работах выдвинуто предположение, что при добавлении в электролит ионов третьего типа в этих скачках возможно их сильное концентрирование. С другой стороны, предложенный подход имеет ограничения, связанные с ресурсоёмкостью расчётов для наноканалов, длина которых многократно превышает ширину.
Существуют подходы [16, 17] , основанные на слабонелинейном приближении, в которых для упрощения задачи вводится много ограничений, например, слабая нелинейность, малые числа Дебая. Кроме этого, модель [17] не учитывает механизм переноса ионов путём адвекции, оставляется только диффузия и электромиграция. Результаты этих работ к тому же слабо согласуются с результатами из [14, 15] .
В настоящей работе изучается упрощённая модель, основанная на усреднённых по поперечному сечению уравнениях Нернста–Планка, Пуассона и Навье–Стокса в приближении ползущего течения. Считается, что изменения вдоль наноканалов являются более медленными, чем в поперечном направлении. Вследствие этого открывается возможность введения малого параметра для асимптотического подхода и выполнения усреднения без предположения слабой нелинейности и других чрезмерно упрощающих допущений. Поведение электролита рассматривается в системе из состыкованных микроканала и наноканала с плоскопараллельными стенками. Такая геометрия, с одной стороны, соответствует принятому предположению (кроме окрестности стыка), а с другой, позволяет качественно сравнивать результаты моделирования с данными других авторов, например, [15] . Область стыка также, хотя и грубо, изображает поверхность ионообменной мембраны в окрестности одной из пор, что делает возможным качественное сопоставление результатов с поведением мембран. В частности, у рассматриваемой системы ожидаемо наличие допредельного и предельного режимов, но не сверхпредельного, который на практике возникает за счёт вихреобразования около селективной поверхности [6] , а характерный размер вихрей многократно превышает размеры пор [18] . Достоверность модели дополнительно проверяется сравнением с численным решением неупрощённых уравнений.
-
2. Постановка задачи
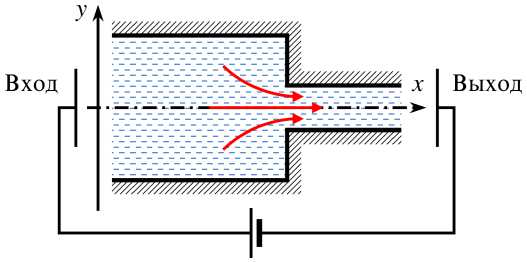
Рис. 1. Схематическое изображение геометрии задачи
Рассматривается течение симметричного одновалентного бинарного электролита в системе, состоящей из прямоугольной нанопоры, выходящей в прямоугольную микропору (Рис. 1) , под совместным действием разности потенциалов и давлений. Стенки пор являются непроницаемыми и полагаются равномерно заряженными. Размер нанопоры предполагается достаточно большим, чтобы к течению была применима гипотеза сплошности. В этом случае движение электролита описывается уравнениями:
dc + dt
~ z +
+ V- j =0,
7+ j
= U c +
DF
-
—c + VФ - DVc + ,
RT
dc dt
~ ^
+ V- j =0,
- j
c
DF
^ ~
= U c- c - VФ - D V c - ,
RT
dV 2 Ф+F ( c + - c - ) =0,
-V P + ~cV U = F(c + - c-) VФ, V^ U = 0,
где (1) — уравнения Нернста–Планка для транспорта ионов, (2) — уравнение Пуассона для распределения электрического потенциала, (3) — уравнения Навье–Стокса для течения жидкой фазы. Последние в силу малости характерных масштабов удобно брать в приближении ползущего течения. В (1)-(3) приняты обозначения: С± — концентрации катионов и анионов; t — время; U — вектор скорости; D — коэффициент диффузии катионов и анионов; F — постоянная Фарадея; R — универсальная газовая постоянная; T — абсолютная температура; Ф — электрический потенциал; d — диэлектрическая проницаемость; P — давление; Д — динамическая вязкость. Здесь и далее тильдой помечены размерные величины. Температура, диэлектрическая проницаемость и вязкость в рассматриваемой постановке полагаются постоянными. На стенках пор задаются условия:
– прилипания жидкости
U = 0 ;
– непроницаемости стенок для ионов
j + • n =j • n = 0;
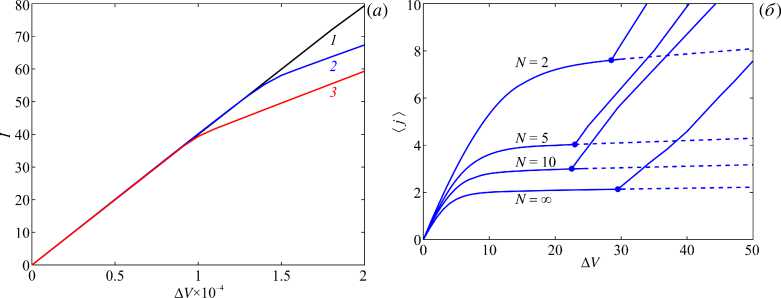
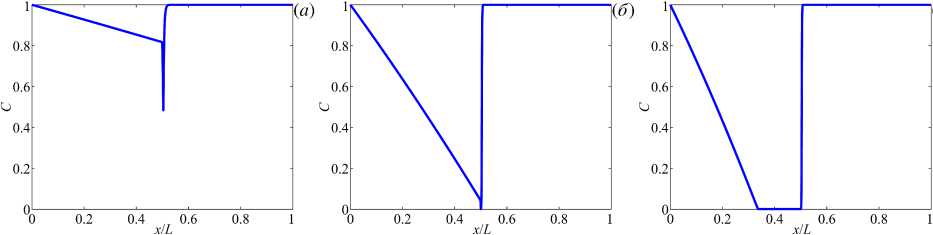
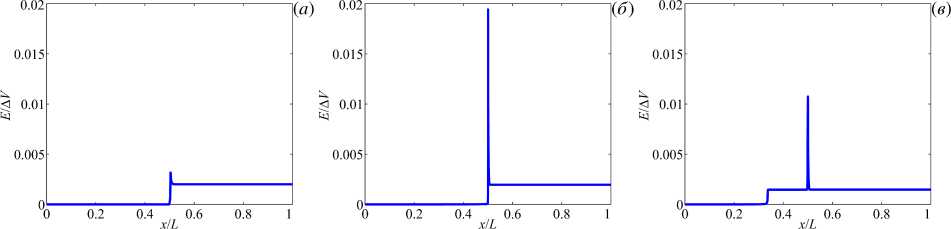
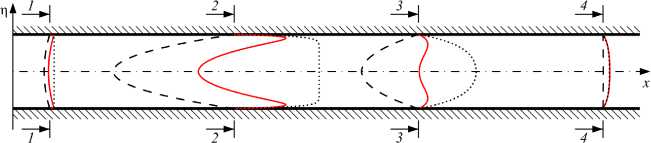
– скачка потенциала dVФ•n= — dj+ dc- Q дх дх ’ dUx дх: Uy = 0, а потенциал отвечает заданной разности потенциалов: Ф = AV. Распределение концентраций ионов в начальный момент времени предполагается равномерным: j+= С = jg. Строго говоря, в канале с заряженными стенками электролит не будет сохранять электронейтральность, и более корректным было бы в качестве начального условия использовать стационарное решение задачи для случая отсутствия внешнего поля и разности давлений (получаемое, например, методом установления из поставленной выше задачи с электронейтральным начальным состоянием). Однако последующие расчёты показали, что в процессе эволюции разница между указанными начальными условиями быстро уменьшается, поэтому для упрощения алгоритма этап установления пропускается. Все величины приводятся к безразмерному виду. В качестве характерных величин берутся: для длины — половина ширины канала на выходе h0; для скорости—D/h0; для времени—h0/D; для динамической величины— Д. Концентрации катионов и анионов относятся к jg, характерным потенциалом служит термический потенциал Ф0= RT/F. Обезразмеренные уравнения (1)-(3) выглядят так: дС+ + Vj+= 0, j+= UC+-С +VФ-VC+, ∂t + Vj-=0, j-=UC-+С-VФ-VC-, ∂t 2£2V2Ф = С --С+, (8) V2U = VP - кVФV2Ф, VU = 0. (9) Здесь е = AD/h0, jD = ^d&o/(2coF) — длина Дебая, к = dФ0/^D} — коэффициент связи гидродинамических и электростатических величин. Краевые условия (4)–(6) переходят в следующие: U = 0, j+ •n=j-•n = 0, eVФ•n = —< Плотность заряда в уравнении (12) нормируется на величину Sq = dФ0/h0, естественным образом получающуюся из обезразмеривания. В начальный момент времени (t= 0) безразмерные концентрации оказываются равными единице: C+= C - = 1. Такой же вид принимает условие для концентраций на входе. Условие на выходе записывается как дС+ _ дС-∂x ∂x Условия для потенциала и скоростей сохраняют свой вид и из соображений экономии места не приводятся. 3. Методика решения Система (7)–(12) может быть непосредственно решена численно, но в этом случае её решение является достаточно ресурсоёмким. Для упрощения постановки предположим, что длина микропоры существенно больше её ширины и изменения в тангенциальном направлении происходят намного медленнее, чем в нормальном, ∂/∂x ≪ ∂/∂y. Нарушением этого условия в малой окрестности стыка пренебрежём (краткое обоснование допустимости этого см. в [14] и цитируемой там литературе). Это даёт возможность воспользоваться интегральным методом типа метода Кармана–Польгаузена [19]: в уравнениях (8), (9) не учитывать тангенциальные производные и найти аналитические решения (8), (9) с явной зависимостью от координаты y, а уравнения (7) проинтегрировать по y с целью нахождения зависимости от x. Далее будут представлены два упрощающих подхода: известный подход Гуи–Чепмена, который справедлив при малых числах Дебая (ε ≪ 1) и подход, основанный на предположении малости поверхностного заряда (σ≪ 1). Подходы являются независимыми. Малое σ позволяет рассматривать любые значения ε, в том числе достаточно большие (разумеется, если не происходит выход за границы применимости континуума), и наоборот. Можно предположить, что каждый из этих подходов уменьшит селективность канала в отношении ионов разных знаков: ионы с зарядом, одноимённым со стенками, не будут встречать заметного сопротивления со стороны электростатических сил либо из-за изначальной малости заряда стенок, либо из-за ослабления создаваемого ими поля к середине достаточно широкого (при ε ≪ 1) канала. Разберём подходы к упрощениям более подробно. Рассмотрим систему, показанную на рисунке 1, как канал Рис. 2. Осесимметричный канал переменного сечения с заряженными стенками переменного сечения (Рис. 2). Зададим профиль стенок функцией y = ±H (x), которая кусочнопостоянна, поскольку претерпевает разрыв на стыке микро- и нанопоры. Для удобства её можно аппроксимировать гладкой функцией с резким изменением в малой окрестности стыка (конкретный вид этой функции дадим в описании численного метода). Вначале, пренебрегая малыми изменениями потенциала в тангенциальном направлении, приведём уравнение Пуассона (8) к виду: 2е2 ТГУ = С --С+. (13) ду2 Для случая σ ≪ 1 уравнение (13) имеет решение: σcosh y C/ε σcosh y C/ε σcosh y C/ε Ф =------т-----^, С+ = С 1--т-----^г , С - = С 1 +------т-----^г , (14) Csinh H C/ε Csinh H C/ε Csinh H C/ε где C является медленно меняющейся функцией переменных x и t: C = C (x,t). При ε ≪ 1 решение уравнения (13) выглядит так + 2 -2 C-=C 1 —Texp ((у — H)^С/е^ С+= С 1-Texp ((у — H)^С/е^ Φ = 4arcth Texp (y-H)√C/ε и справедливо при 0 T = 1+ 2VC\ VC σσ Из уравнения неразрывности dU/dx+dV/ду = 0 при д/дх ^ д/ду следует, что нормальная компонента скорости V мала по сравнению с тангенциальной U: V ≪ U. Соответственно, уравнения Стокса (9) сводятся к одному уравнению: ∂2U ∂P ∂2Φ ∂y2∂x κ ∂y2 Поскольку тангенциальная напряжённость электрического поля E ≡ -∂ Φ/∂ x, входящая в уравнение (16), существенно зависит от внешнего поля, она рассматривается как неизвестная функция, которую определим позднее. С другой стороны, в члене ∂2Φ/∂y2эта зависимость мала, поэтому в него можно подставить значение Φ, найденное из (14) или (15). В дальнейших выкладках под Φ будет пониматься именно это асимптотическое значение, а не полный электрический потенциал. Тангенциальная скорость U является быстро меняющейся функцией y , но медленно меняющейся функцией x (и t). Представим U в виде суперпозиции напорной (Up) и электроосмотической (Ue) частей, каждая из которых удовлетворяет краевым условиям по y . Тогда уравнение (16) распадется на два: Up =9 (У2 - H 2), Ue = кЕ (Ф—Z). 2 дх Здесь Z — значение потенциала Ф на боковых стенках у = ±Н, которое при е ^ 1 приобретает физическое значение дзета-потенциала. Напорная и электроосмотическая части скорости создают расходы по сечению канала. В силу симметрии задачи удобно рассматривать половины этих расходов, соответственно, Qp и Qe : ∂P H3 Qp=-дх • V, H Qe = KEj (Ф-Z )dy. Из физических соображений потребуем, чтобы суммарный полурасход Q = Qp + Qe не зависел от х. Это условие позволяет выразить в соотношении (18) неизвестную функцию ∂P/∂x через неизвестную постоянную Q: H кЕ (ф-Z )dy-Q 1 . (19) Тогда с учётом (19)Up в соотношении (17) примет следующий вид: (H \ Q-кЕ^Ф-Z )dy](H2- У2). Теперь проинтегрируем уравнения транспорта ионов (7). Воспользовавшись условиями непроницаемости стенок для обоих типов ионов и вынеся дифференциальные операторы из-под знаков интеграла, получим: HH HH fC ±dy + fUC ± dy ± д' Е I с ±dy = /C ±dy - ^ ^C ±\y=H Y ∂t ∂x ∂x ∂x2 ∂x ∂x 00 00 Подстановка в (20) найденных выше решений позволяет получить уравнения относительно двух неизвестных функций — C и E, и параметра Q. Соответствующие выкладки опустим, только укажем, что вычитание уравнения (20), записанного для C-, из уравнения (20) для C+приводит к уничтожению производной по t, а оставшееся обыкновенное дифференциальное уравнение после однократного интегрирования по x переходит в алгебраическое уравнение. При а ^ 1 итоговое уравнение принимает вид: (HC) + (QC-еаЕ) = (h^c\ (21) ∂t ∂x ∂x ∂x где E = M/N, a M и N задаются соотношениями M =6032 (ZH - С ) +2ZCdH +I, N = - H2 (CH - C )2 + k{c2H+^C - CH. 2)+2CH. (22) Величина I в (22) — это постоянная интегрирования, которая имеет физический смысл электрического тока, протекающего через канал. Случай e< 1 порождает более сложное уравнение, которое содержит специальную функцию — дилогарифм Li2(±T): д 2HCCJCГ^Сё-1)- -^{EC^НС-^VC(^1 + ^_ 1)] } + +ГI 1t3Qp CHH33 — 4e2ln(1-T2) — (Li2(1 —T)+Li2(1+T)) j+ dx [H3 [3 ' CС J J h(1-T)-(1+T)-■ +CT-T2 J}-(cE)= =■' I2HC+wc (Xf-1!1-a ■+2C) |HV dx2 4C d \ ox \ dx J где Qp и ζ определяются через потенциал, заданный по формуле (15). Функции M и N, через которые находится E, будут иметь вид, структурно аналогичный (22), который из соображений экономии места здесь не приводится. Для упрощённых уравнений (21) и (23) роль краевых условий для потенциала и скорости выполняют два параметра: ток I и расход Q. Отметим, что эти параметры можно заменить, соответственно, на разность потенциалов ∆V и разность давлений ∆P : LLL ^V = / Edx.I = U- -jM—Idx]//dx. L / L H \ -.P = 1 ^. Q = ( (ф-с.W-4P У/3ddx. 0 000 где L — безразмерная длина канала. В расчётах, описываемых ниже, задавалась пара ∆V и Q, если явно не оговорено иное. Для решения полученных уравнений, как полной системы (7)–(12), так и её упрощений (21) и (23), был разработан численный метод, основанный на конечно-разностной аппроксимации. Пространственные производные задавались центральными разностями 2-го порядка на смещённых сетках, для интегрирования по времени использовался полунеявный метод Рунге–Кутты 3-го порядка точности [20]. В качестве неявной части рассматривался якобиан численного оператора. Для контроля точности метода выполнялось удвоение числа узлов сетки, а для контроля влияния граничных условий — удвоение длины канала (с одновременным удвоением разности потенциалов с целью сохранения неизменной средней напряжённости поля). Уравнения (8), (9) в неупрощённой постановке решались прямым методом, сводящимся к решению систем линейных алгебраических уравнений. Прямоугольная геометрия позволяет ставить граничные условия в явном виде, без использования метода погружённых границ. Для уменьшения вычислительной сложности решения применялось разложение по собственным функциям и сращивание решений на стыке микро- и наноканала. Этот приём позволил свести решение линейной системы с разреженной матрицей к многократному применению модифицированного метода прогонки. Тем не менее, вследствие жёсткости системы уравнений производительность такого алгоритма оказалась недостаточной, поэтому он использовался главным образом для верификации результатов, полученных на основе упрощённого подхода. 4. Результаты моделирования Расчёты проводились в канале с заданным профилем H (x) = b+R+bR th 2 2 γ x L который имитирует стык микроканала шириной R и наноканала шириной 1 при x = L/2. Были взяты значения L = 1000, R = 1000, y = 1. Бралось к = 0.26, соответствующее раствору хлористого калия; плотность заряда стенок для простоты полагалась постоянной. Значение Q задавалось двумя способами: как фиксированное значение Q = 0.5 ив виде линейной зависимости от напряжённости поля: Q = 3.5 х 10-5AV, имитирующей электроосмотический поток. Вычисления показали, что при max(|a|,е) < 0.3 разное задание Q приводит к незначительному количественному отклонению, а выбор уравнения (21) или (23) даёт результаты, совпадающие с графической точностью. В дальнейшем, если не оговорено иное, будут приводиться решения уравнения (23) при Q = 3.5 х 10-5AV. На рисунке 3а представлена типичная вольт-амперная характеристика, которая для каждого из указанных в легенде наборов параметров системы состоит из двух прямых линий, соединённых небольшим переходным участком. При изменении параметров системы — величины заряда стенок, расхода электролита и числа Дебая — наклоны прямолинейных участков визуально не изменяются, сдвигается только точка перехода между ними. Увеличение указанных параметров приводит к уменьшению напряжения перехода и наоборот. Рис. 3. Вольт-амперные характеристики стыка микро- и наноканала (а); частично селективных мембран [21] (б) Можно утверждать, что модель качественно повторяет поведение ионоселективной мембраны. Начальный участок, очевидно, представляет омический (допредельный) режим, а при увеличении разности потенциалов скорость нарастания тока уменьшается — это соответствует предельному режиму. Для сравнения приведём вольт-амперные характеристики модельных катионообменных мембран [21] (Рис. 3б), где величина N характеризует селективность мембраны (N = 0 означает абсолютно неселективную поверхность, а N = сю — идеальную селективную). Скорость нарастания тока в предельном режиме увеличивается с уменьшением селективности, что хорошо согласуется с предположением о слабой селективности рассматриваемого канала. Также подтверждается отсутствие у системы сверхпредельного режима. На рисунке 4 приведены профили функции C(x) для различных режимов при € = 0.3 и а = -0.3 (она соответствует графику 3 на Рис. 3а). Переход от допредельного режима к предельному характеризуется резким уменьшением концентрации ионов и, как следствие, проводимости системы в окрестности входа в наноканал. Расчёты, выполненные для неупрощённой системы, показывают качественно аналогичное поведение суммарной концентрации ионов и одновременный рост плотности заряда в этой области. Полученные результаты качественно согласуются с результатами работы [15]. Напряжённость E(x) также демонстрирует скачок на стыке (см. Рис. 5). (в) Рис. 4. Изменение C (x) вдоль канала: допредельный режим, AV = 2000 (а); переход к предельному режиму, AV = 10000 (б); развитый предельный режим, AV = 20000 (в) Рис. 5. Изменение E (x) вдоль канала: допредельный режим, AV = 2000 (а); переход к предельному режиму, AV = 10000 (б); развитый предельный режим, AV = 20000 (в) На схеме, приведённой на рисунке 6, показано распределение полной продольной скорости U, её электроосмотической (Ue) и напорной (Up) компонент в разных точках канала. Расчёт выполнен для уравнения (21) при нулевой разности давлений, е = 1 и а = - 0.1. Для удобства восприятия поперечная координата нормирована на толщину канала: п = y/H. Рис. 6. Схематическое изображение профилей скорости в разных сечениях канала: 0.100 (сечение 1-1); 0.450 (2-2); 0.503 (3-3); 0.900 (4-4); общая скорость показана сплошной линией, напорная компонента – штриховой линией, электроосмотическая – точками Недалеко от входа (сечение 1-1) за счёт электроосмотической компоненты скорости жидкость движется вперёд и тем самым создаётся сопротивление, выражающееся в возникновении отрицательной напорной компоненты Up < 0. Результирующая скорость U положительна, но имеется противонаправленное движение по оси микроканала и сонаправленное пристенное движение. При подходе к месту соединения микро- и наноканала (сечение 2-2) компоненты, как электроосмотическая, так и напорная, увеличиваются по модулю, но сохраняют своё направление. Профиль общей скорости позволяет говорить о вихреобразовании в данном месте: этот вывод соответствует экспериментальным данным из [18] и подтверждается численным решением неупрощённых уравнений. На входе в наноканал (сечение 3-3) обе компоненты резко уменьшаются по модулю, но также сохраняют направления. По мере движения жидкости к выходу напорная компонента стремится к нулю (сечение 4-4). 5. Заключение и дискуссия Численно изучалось поведение разбавленного электролита в системе из состыкованных микроканала и наноканала с заряженными стенками под действием давления и разности потенциалов в рамках гипотезы сплошной среды. Использованы упрощения, основанные на асимптотическом разложении по единственному малому параметру — числу Дебая, или плотности заряда стенок; в последнем случае модель допускает рассмотрение наноканалов, ширина которых сопоставима с толщиной дебаевского слоя. Численно получены основные характеристики течения и распределения ионов. Предложена аналогия между рассмотренным каналом и порой ионообменной мембраны, с её помощью показано, что допредельный и предельный режимы работы мембраны проявляются также для её отдельной поры и, следовательно, не являются системным свойством. Результаты демонстрируют удовлетворительное соответствие численному решению неупрощённых уравнений и экспериментальным данным. Предложенная в работе упрощённая модель допускает несколько важных обобщений. Во-первых, как сказано в разделе 3, профиль стенок не ограничивается особенностью в виде стыка микро-и наноканала, а может иметь произвольную форму (задаваемую функцией одной переменной), причём точность задания профиля зависит только от числа узлов сетки. Как следствие, модель допускает изучение нанопор наперёд заданного переменного сечения. Предположительно их поведение также будет качественно выглядеть как поведение частично селективных мембран до тех пор, пока не произойдёт переход к сверхпредельному режиму. Это утверждение сделано на основе выводов работы [21], где в рамках другой модели показано качественное совпадение вольт-амперных характеристик мембран разной степени селективности. Аналогично, предложенный численный метод допускает рассмотрение стенок с неоднородным распределением заряда (функции σ), но изучение влияния этого распределения на поведение системы осталось за рамками работы. Во-вторых, рассмотрение электролита с большим числом ионов сводится к добавлению к уравнению (1) аналогичных уравнений с дополнительными коэффициентами в правой части (относительными коэффициентами диффузии и зарядовыми числами), при этом численный алгоритм принципиально не меняется ни для упрощённой, ни для полной постановки. В частности, авторами выполнены предварительные расчёты для электролита со взвешенными сильно заряженными частицами, показавшие возможность управления движением этих частиц. Аналогичным образом модель обобщается на случай течения с диссоциацией/рекомбинацией ионов. Отдельный интерес представляет случай околонулевого приложенного напряжения. Нарушение электронейтральности электролита в системе, вызванное зарядом стенок, приводит к возникновению в ней ненулевого электрического тока и порождает разность потенциалов между входом и выходом — потенциал течения (его величина мала и из-за выбранного масштаба не видна на графике рисунка 3а). Предложенная модель показывает, что концентрация ионов электролита на выходе в таком режиме отличается от входной и может быть как меньше её, так и больше в несколько раз. Рассмотрение этого и других упомянутых выше эффектов — предмет отдельного исследования. Работа выполнена при поддержке Российского научного фонда, проект № 22-29-00307 .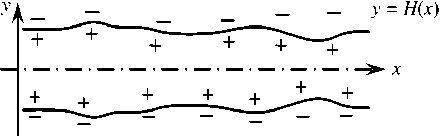
Список литературы Моделирование наноканалов в синтезированных мембранах
- Chang H.-C., Yossifon G., Demekhin E.A. Nanoscale Electrokinetics and Microvortices: How Microhydrodynamics Affects Nanofluidic Ion Flux // Annual Review of Fluid Mechanics. 2012. Vol. 44. P. 401–426. DOI: 10.1146/annurev- fluid- 120710-101046.
- Han W., Chen X. A review: applications of ion transport in micro-nanofluidic systems based on ion concentration polarization // Journal of Chemical Technology & Biotechnology. 2020. Vol. 95. P. 1622–1631. DOI: 10.1002/jctb.6288.
- Siwy Z., Gu Y., Spohr H.A., Baur D., Wolf-Reber A., Spohr R., Apel P., Korchev Y.E. Rectification and voltage gating of ion currents in a nanofabricated pore // Europhysics Letters (EPL). 2002. Vol. 60. P. 349–355. DOI: 10.1209/epl/i2002-00271-3.
- Mikhaylin S., Nikonenko V., Pismenskaya N., Pourcelly G., Choi S., Kwon H.J., Han J., Bazinet L. Howphysico-chemicalandsurface properties of cation-exchange membrane affect membrane scaling and electroconvective vortices: Influence on performance of electrodialysis with pulsed electric field // Desalination. 2016. Vol. 393. P. 102–114. DOI: 10.1016/j.desal.2015.09.011.
- Левич В.Г. Физико-химическая гидродинамика. М.: Физматлит, 1959. 700 с.
- Rubinstein I., Zaltzman B. Electro-osmotically induced convection at a permselective membrane // Physical Review E. 2000. Vol. 62. P. 2238–2251. DOI: 10.1103/PhysRevE.62.2238.
- Demekhin E.A., Nikitin N.V., Shelistov V.S. Direct numerical simulation of electrokinetic instability and transition to chaotic motion // Physics of Fluids. 2013. Vol. 25. 122001. DOI: 10.1063/1.4843095.
- Ouyang W., Ye X., Li Z., Han J. Deciphering ion concentration polarization-based electrokinetic molecular concentration at the micro-nanofluidic interface: theoretical limits and scaling laws // Nanoscale. 2018. Vol. 10. P. 15187–15194. DOI: 10.1039/c8nr02170h.
- Abu-Rjal R., Chinaryan V., Bazant M.Z., Rubinstein I., Zaltzman B. Effect of concentration polarization on permselectivity // Physical Review E. 2014. Vol. 89. 012302. DOI: 10.1103/PhysRevE.89.012302.
- Ganchenko G.S., Kalaydin E.N., Schiffbauer J., Demekhin E.A. Modes of electrokinetic instability for imperfect electric membranes // Physical Review E. 2016. Vol. 94. 063106. DOI: 10.1103/PhysRevE.94.063106.
- Demekhin E.A., Ganchenko G.S., Kalaydin E.N. Transition to electrokinetic instability near imperfect charge-selective membranes // Physics of Fluids. 2018. Vol. 30. 082006. DOI: 10.1063/1.5038960.
- Probstein R.F. Physicochemical Hydrodynamics: An Introduction. Wiley, 1994. 416 p. DOI: 10.1002/0471725137.
- Chang H.-C., Yeo L.Y. Electrokinetically-driven microfluidics and nanofluidics. Cambridge University Press, 2010. 526 p.
- Computational continuum mechanics. 2024. vol. 17, no. 1. pp. 5–14 13
- ISSN: 1999-6691, e-ISSN: 2782-3709 DOI: http://doi.org/10.7242/1999-6691/2024.17.1.1
- Mani A., Zangle T.A., Santiago J.G. On the Propagation of Concentration Polarization from Microchannel–Nanochannel Interfaces Part I: Analytical Model and Characteristic Analysis // Langmuir. 2009. Vol. 25. P. 3898–3908. DOI: 10.1021/la803317p.
- Zangle T.A., Mani A., Santiago J.G. On the Propagation of Concentration Polarization from Microchannel–Nanochannel Interfaces Part II: Numerical and Experimental Study // Langmuir. 2009. Vol. 25. P. 3909–3916. DOI: 10.1021/la803318e.
- Mani A., Bazant M.Z. Deionization shocks in microstructures // Physical Review E. 2011. Vol. 84. 061504. DOI: 10.1103/ PhysRevE.84.061504.
- Yaroshchuk A. Over-limiting currents and deionization “shocks” in current-induced polarization: Local-equilibrium analysis // Advances in Colloid and Interface Science. 2012. Vol. 183/184. P. 68–81. DOI: 10.1016/j.cis.2012.08.004.
- Nikonenko V.V., Pismenskaya N.D., Belova E.I., Sistat P., Huguet P., Pourcelly G., Larchet C. Intensive current transfer in membrane systems: Modelling, mechanisms and application in electrodialysis // Advances in Colloid and Interface Science. 2010. Vol. 160. P. 101–123. DOI: 10.1016/j.cis.2010.08.001.
- Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974. 712 с.
- Nikitin N. Third-order-accurate semi-implicit Runge–Kutta scheme for incompressible Navier–Stokes equations // International Journal for Numerical Methods in Fluids. 2006. Vol. 51. P. 221–233. DOI: 10.1002/fld.1122.
- Кирий В.А., Шелистов В.С., Калайдин Е.Н., Демёхин Е.А. Гидродинамика, электроосмос и электрокинетическая неустойчивость в несовершенных электрических мембранах // Доклады Академии наук. 2017. Т. 473, № 6. C. 659–663. DOI: 10.7868/s0869565217120076.


