Моделирование нелинейного развития возмущений в тонком жидком слое при волнообразовании

Изучение систем физико-химической гидродинамики с поверхностью раздела между жидкой и газовой фазами обусловлено, прежде всего, их прикладным значением [1, 2]. Технологические процессы, связанные с переносом тепла и массы через поверхность раздела, широко распространены в химической, нефтехимической, энергетической, металлургической, пищевой и других отраслях промышленности. Тепломассообменные аппараты, в которых реализуется течение тонких жидких пленок под действием силы тяжести, весьма перспективны в химической, нефтехимической технологии. В жидких пленках обеспечиваются высокие скорости переноса тепла и массы в сочетании с малой толщиной пленки, но то же время приходиться решать сложнейшие вопросы, связанные с межфазной неустойчивостью, влиянием на нее разнообразных физикохимических факторов, обусловленных, например, наличием градиентов температуры, концентрации вещества на межфазной поверхности, фазовыми переходами. Процессы течения жидких пленок, обдуваемых газовым потоком, также представляют значительный интерес для науки и проектирования современной пленочной аппаратуры.

Рассмотрим течение тонкого слоя вязкой несжимаемой жидкости (жидкой пленки) толщиной δ под действием силы тяжести по твердой наклонной плоскости, сопровождающееся обдувом ее свободной поверхности парогазовым потоком. Введем прямоугольную систему координат OXYZ , плоскость OXZ связана с поверхностью, по которой движется пленка, ось OX направлена по течению пленки, ось OY – по нормали в пленку жидкости (рис. 1).

Рис. 1. Схема течения жидкой пленки

Математическая модель течения трехмерной жидкой пленки толщиной 3 по твердой наклонной поверхности под действием силы тяжести, сопровождающаяся обтеканием ее свободной поверхности парогазовым потоком произвольного направления, представляет собой систему уравнений Навье–Стокса и уравнения неразрывности с граничными условиями, учитывающими влияние процессов тепломассопереноса, имеет вид [3]:

uuu —+ + u+ —+ + v+ — + д t + + д x + т д у +	u + w +     : д z +
д к +     д к +     д к +      д к + + u+-- + v+ --+ w+--- — д t +     + д x +т+ у +      <) z +
д w+ д w+ д w+ —+ + u+ —+ + v+ — + д t + + д x + т д у +	д w+ -+ w + — д z +

1 ( д ² u

д u₊   д V,    д w₊

^+ + Т+ +   = °, ду+   дz+

д x.

+

y = 0:

y = 3 :

Re

2 д u ₊ д 3 ₊ д x ₊ д x ₊

Re

д P ₊        1

д x₊^{+ x +} Re ( д x +

+

д ² и ₊

+ ^

+

д ² и ₊

д z + У

*+ + F +-1

^д y +

P + F +

z

д z ₊

u ₊ = w ₊ = °,

2 д к ₊ д 3 ₊ д у ₊ д x ₊

д 3

+ M —- + N д x ₊

' ^{д 2} и +

к

д x +

+

2 д w + д 3 + д z ₊ д z ₊

2 ^{д V} + ^{д 3} + ^д У + ^{д z} +

P + =А^ к

+

Re ^д у ₊

Re

к д 2 v+		д 2 к + д у + 2 +	д 2 V + д z + У	,
к	д x +
	д 2 w +	+32 w +	+^ 1
e	к д x +	д у + 2	д z	2 + У

^V + = V ° ;

' д к

+

дu.

,

к дx+ rw2- дx+ дz+ J

д и.

+     । .           + ^д w ⁺

'+

д 3 ₊

^д У + ) ^{д z} +

^{+ T} x = °;

'+

_к д z ₊ д x ₊

^{д w} + ₊ ^{д к} + | +9 3 + 1 ^{д u} + ₊ - +

к ^д у +    ^{д z} + ) ^д x +

+ M ³ + N ^{д z} +

^{д 3} + Г ^{д u} + , ^{д V} +

+

д x ₊ к д у ₊ д x ₊

■+

д w ₊

_к д z ₊ д x ₊

+

+

22 д w.      д u.

+ к дz +   дx+дz + J

^{д 3} + k 3 w + ₊д к +

+

^д z + к ^д У +

^{д z} +

+ T z = 0;

^{- о} +

Г д 2 3 д ² 3 )

к J

+

+ P ° - sign A T

P i - 1

P 2

( Re • Pr • Ku ) 2 3 2 ’

д 3

V = V д t ₊

_s

д 3

u+ дx+

_s

д3 w+ — + дz+

Re • Pr • Ku 3

.

Безразмерные величины в (1–6):

^u +

u

—, V+ u0

v

—, ^w + u ₀

w

u ₀

проекции скорости на соответст-

t • u_n вующие оси координат; t = —° 3 °

время; x ₊

x

=V

у + =^, ³ °

z 3 z ₊ = — - переменные ; 3 ₊ = — ^т 3 ° ^т 3 °

„     „                 П   u03р     „ „ толщина жидкой пленки; Re = -°—°число Рейнольдса; Fx

= gx3

u 0 ²

, F y =

g-³! _F = , z u 0 ²

P проекции числа Фруда на соответствующие оси координат; Р+ = —- давление;

P u _° ²

N =

_: g z ³ ° u 0 ²

k + e

P ³ ° u °

T параметр поверхностной вязкости; T _x = — x y, T _z = P u _° ²

M = M T + M _K - параметр Марангони: M-

до ГдT

^T z

P u _° ² ° А

проекции касательного

напряжения;

T д T °

к

, M ду ) у=3Pu °

■ =д £ д K 1 . K д K д3 p u °2 ’

pc_o и Pr = i-Pp-X

Г                                           СУ число Прандтля; Ku =---- - число фазового перехода; у = —г--параметр поверхностного

С р ^Д T                                   р и 02 ^ 0

натяжения. Здесь и ₀ - средняя скорость основного течения жидкой пленки, 5 ₀ - толщина пленки в невозмущенном состоянии. В процессе конденсации sign Д T = 1, а в процессе испарения sign Д T = - 1.

Рассмотрим развитие на поверхности жидкой пленки возмущений, принадлежащих непрерывной полосе волновых чисел:

к _о ,+Д к, к ,+Д к- ^v х х ^v z z

V = J J F ( к x ) exp { i ( к х х + T_zz - to t ) } dk x dk _z = A exp { i ( к 0 х х + к 0 z z - to ( к 0 ) t ) } ,    (7)

ко _-Дк_ ко _-Дк, ^ х х ^ z z где к0 - центр волнового пакета; to = tor + itoi;

Д к _ Д к „ xz

г

A = J J F ( к o x + ^ к s ) exP ' i ^х + 5T_zz

-Д к _у -Д к- xz

1 д СО„

2 "l^²

к       7к.

1 д СО_У

21    1

zk

д tor

I д кх )t х x  k0

дto)

I д к₂ V ^z k ₀

Iд к х д к ₂ I, k ₀

З к_х 3 k_t - £ ² to t xzi

• d З k _x d З k _z + о £ ³ )

при следующих допущениях: Д к ^ - ширина полосы волновых чисел Д к ^ = о £ ) ; инкремент to i = £ 2 0 )1 = о £ ² ) .

Здесь F ( к ^ ) - Фурье-компонента разложения, к ^ - волновой вектор возмущений, k x и k _z - его проекции на оси ОХ и OZ соответственно, £ - малый параметр.

Для амплитуды A огибающей волнового пакета получено нелинейное параболическое уравнения, коэффициенты которого в явном виде выражаются через параметры волнового течения трехмерной жидкой пленки: инкремент, частоту и их производные первого и второго порядков, –

д A   i дй 1 д A   i дй ! д A

i д to r

2 к д к

x ²

+ i

^д 2 « л д ² A

д k X

) д х 2

2 id to — ---y- + i

2 1 д T_z ²

z

^д 2 « л д ² A

д ^ 7

д z 2

- i

( д2to    . д2to r + i—^

д ² A

xz

xz 1

Нелинейное параболическое уравнение (8) для амплитуды A огибающей волнового пакета, развивающегося по времени на поверхности неизотермической жидкой пленки, относится к одной из базовых моделей нелинейных сред (типа модели Гинзбурга–Ландау). Коэффициенты уравнения учитывают фазовые переходы (конденсация, испарение) на поверхности трехмерной жидкой пленки и включают такие физико-химические факторы, как поверхностную вязкость, неоднородность поверхностного натяжения, силу тяжести, касательное напряжение на поверхности раздела газ-жидкость.

Вычислительные эксперименты, связанные с неустойчивостью жидкой пленки по отношению к возмущениям, волновой вектор которых к _s направлен под углом а к оси ОХ :

кs = Vкх2 + к2 , tga = Tz, kx проведены для диапазона чисел Рейнольдса Re < 20. Необходимость таких исследований связана с интенсификацией процессов тепло- и массообмена в жидких пленках, повышения эффективности, экологической безопасности и надежности пленочных аппаратов.

Дисперсионное уравнение to(a7кх + a9Tz + i) + aiкх + a2кхк^ + a2к7. -

^{- a} 10 ^к 12 ⁺ a ll ^1Т х ^{+ a} 12 ^{к -}

a ₄ ik _x ³ 1

a ₅ ik _z ³

a 6 k x ²

a ₈ k _x k _z

Re • Pr • Ku

= 0,

где to = tor + ito,, позволяет рассчитать волновые характеристики: tor - частоту, to, - инкремент, фазовую скорость c = —-, а также производные, входящие в уравнение (8).

r k

Коэффициенты дисперсионного уравнения (9) имеют вид:

Re • о      _                 Re2 F_N       Re2 F_N* !

a 1 =-- , a ₂ = 2 a 1 , a 3 = a 1, a 4 =-- x— , a 5 =-- ^z —, a 6 = a 6 + a 6 ,

= _ReiZyL _ ReM + _! Re3f T + F), a 1 = 2 Re • sign AT----- a7 = 35 Re2Fx ,

3        2     40 x ⁽ x x ) 6 3              ( Re • p_r • Ku ) ²

a 8 = Щ ^R e ^{FxFz + R} e ( ^{Fz T x +} F T ) , a 9 = ^ ^R e ^F - , a 10 = a 10 ⁺ a W ,

^a *0 = e-F y- - Re^M ⁺ -3 ^{Re 3} F z (^T z ⁺ F z ) , ^a W = ^{2 Re} • sign ^A T----- ^C ---, a ll =- ^Re • ( F x ^{+ T} x ) ,

Волновые характеристики (инкремент to i и фазовая скорость c _r ) возмущений изображены на рис. 2 и рис. 3 соответственно.

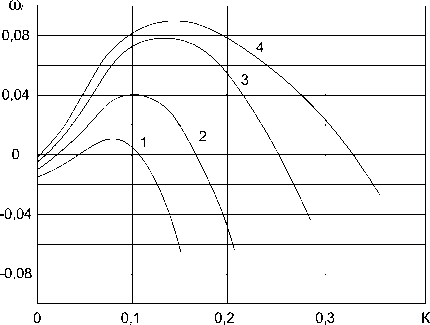
Рис. 2. Зависимость инкремента от волнового числа:

1 – Re = 7; 2 – Re = 10; 3 – Re = 15; 4 – Re = 20

На каждой кривой инкремента (рис. 2) можно отметить наличие характерных точек:

перегиба, которому соответствует значение волнового числа k _п ;

максимального значения инкремента, который обозначим k _{to ;max} ;

соответствующих нейтральной устойчивости ( to , = 0 ) , волновые числа которых обозна-

^чим k to , =0 .

Совокупность точек ktoj =0 для исследуемого диапазона чисел Рейнольдса образует кривую нейтральной устойчивости (рис. 4, кривая to = 0), а точек к - образует кривую максималь-д                            toi max ного роста возмущений (рис. 4, кривая to, max).

Фазовая скорость (рис. 3) в области неустойчивости жидкой пленки для каждого числа Рейнольдса имеет минимальное значение ( c r _min ) , которое соответствует волновому числу к _{й )[} max . Фазовая скорость c _{r min} падает с ростом числа Рейнольдса.

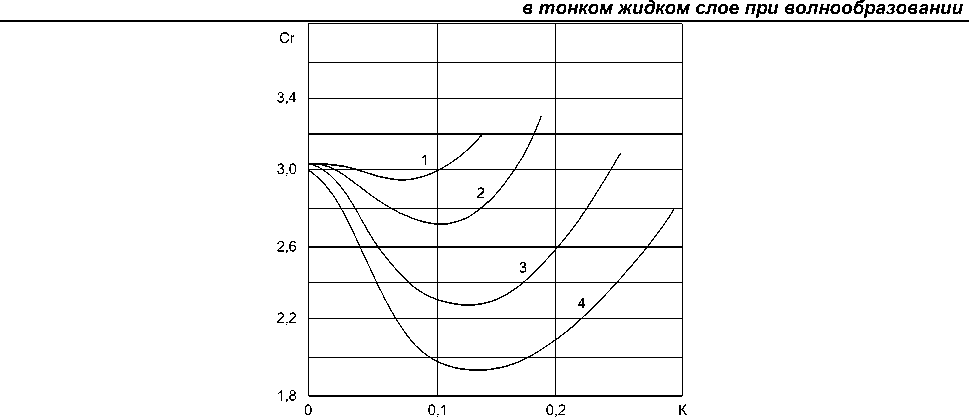
Рис. 3. Зависимость фазовой скорости от волнового числа:

1 – Re = 7; 2 – Re = 10; 3 – Re = 15; 4 – Re = 20

В ходе вычислительных экспериментов найдены области существования волновых режимов жидкой пленки при свободном стекании, конденсации, испарении, а также при воздействии физико-химических факторов модели (1)–(6). На рис. 4 представлена область существования волновых режимов вертикальной жидкой пленки в процессе испарения. Для чисел Рейнольдса Re > 10 вблизи нейтральной кривой существует область, в которой проявляется эффект направленного переноса энергии по спектру волнового пакета и его смещение в направлении гармоники максимального инкремента. В окрестности ω _{i max} существуют стационарные монохроматические режимы волновых течений жидких пленок, что также отмечалось и в экспериментах [1, 2].

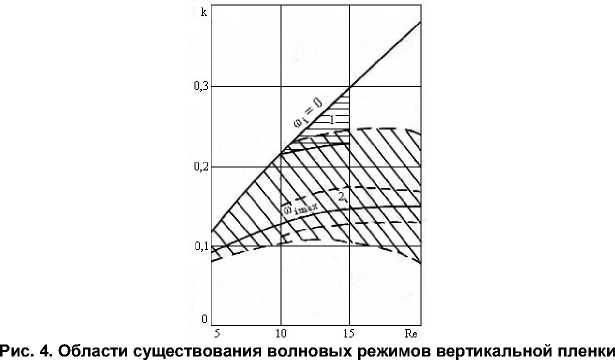
Расчет коэффициентов β ₁ и β ₂ при нелинейном члене уравнения (8), характеризующих нелинейное затухание возмущений ( β ₁ ) и зависимость фазы от амплитуды ( β ₂ ), позволил определить:

• –    нелинейное взаимодействие возмущений в окрестности ω _{i max} (рис. 4, область 2) таково, что наблюдаются незначительные изменения коэффициентов β ₁ , β ₂ , они практически сохраняют свое значение в области 2;

• –    линейную зависимость фазы от амплитуды для чисел Рейнольдса Re <  8 и нелинейную для Re ≥ 8 .

Для волновых пакетов в окрестности гармоники максимального инкремента свойственна самая высокая степень неустойчивости системы. В рассматриваемой окрестности повышена интенсивность формирования структуры течения в приповерхностных слоях, степень ее развитости. Формы волн вертикальной жидкой пленки воды при неоднородности поверхностного натяжения представлены на рис. 5, кривая 1.

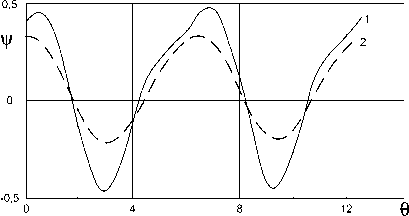
Рис. 5. Форма волны при Re =15:

• 1    – M =1, N =0; 2 – M =1, N =1

Наличие в жидкой пленке нерастворимых поверхностно-активных веществ, таких как масла, жиры (параметр N ), вязкость которых больше вязкости воды и возрастает с увеличением их молекулярной массы, при движении жидкого слоя приводит к возникновению сил поверхностной вязкости, качественно влияющих на волновые характеристики течения трехмерной жидкой пленки, границу устойчивости. Пленки нерастворимых поверхностно-активных веществ, обладая большим внутренним трением, при движении тонкого слоя вязкой жидкости забирают значительную часть его энергии, что ведет к уменьшению скорости возмущенного течения и сглаживанию профиля волн (рис. 5, кривая 2).

Представим комплексную амплитуду A в виде суммы амплитуд мод

^

A = a ₀ exp i O 0 + ^ ( a _n1 exp i O _n1 exp ink 1 x + a n 2 exp i O n 2 exp( - ink 1 x ) ) .             (10)

n = 1

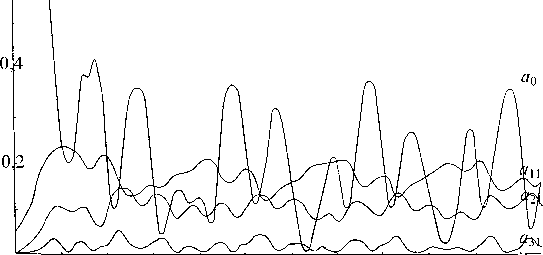
Амплитуды гармоник (10) для исследуемой диспергирующей системы с зависимостью фазы от амплитуды в условиях формирования монохроматической волны изображены на рис. 6.

a

0          2          4          6          8          10 т

Рис. 6. Амплитуды мод (10)

Представленная нелинейная теория волнового течения жидкой пленки позволяет исследовать характер нелинейного взаимодействия возмущений, учитывая различные условия: изменение угла наклона поверхности стекания, неоднородность поверхностного натяжения.