Моделирование параметров молнии и грома мощным электрическим разрядом и излучением

Согласно [1, 2], ежегодно на Земле происходит свыше 30 млрд. грозовых разрядов, которые обычно возникают внутри грозовых облаков, между ними и реже между облаком и землей или ионосферой. В отдельном грозовом облаке электрическая энергия может достигать 1010-1011 Дж, а в каждой молнии длительностью до 0,1 сек, обычно выделяется энергия 1071010 Дж. При ударе молнии в землю разряд происходит в полях около 3 кВ/см, что на порядок меньше пробойного поля для воздуха. Сначала идет лидер с током около 100 А, потом от земли обратный разряд. Эта главная стадия молнии с током до 100 кА, температурой Т = 30 - 25 кК и скоростью 0,1-0,3 от скорости света вызывает ударную волну, действие которой сопровождается громовыми раскатами. С помощью гроз реализуется взаимодействие верхних и нижних геосфер Земли путем обмена запасаемой в них механической и электрической энергии. Поэтому полезны модельные исследования этого процесса, позволяющие получать его количественные оценки. Условия применения электрических разрядов конденсаторных батарей для лабораторного моделирования газодинамических процессов при грозах без ветра рассмотрены в [9]. Критерии моделирования получены из определяющих модельные и натурные процессы МГД уравнений.

Ниже рассмотрены методы экспериментального моделирования молнии и грома разрядом конденсаторных батарей и импульсным лазерным облучением преград в режиме плазмообразования, включая условия бури на основе общих критериев моделирования полученных из МГД уравнений в более широком диапазоне параметров.

Критерии и методы моделирования.Для моделирования молнии электроразрядной и лазерной плазмой применялись полученные из МГД уравнений следующие безразмерные критерии моделирования: п=?т/?0, л RiER) ', с1/?0(Е/?0)1/3, ст/(Е/?0)1/3, L/R. Здесь Pm/P0 - отношение максимального давления ударной волны (УВ к атмосферному, E – энергия плазмы, I, τ – удельный импульс и длительность положительной фазы УВ, с - скорость звука, L, R длина разряда и расстояние до него. Размерный критерий j2/σ определяет равенство удельных мощностей энерговклада в молнии и в разряде батареи. Условие (- div q)=(j2/σ) определяет равенство удельных мощностей энерговклада в лазерной плазме и молнии, где j – плотность тока, σ – проводимость плазмы, q – плотность подводимой энергии излучения. Использованная система МГД уравнений имеет вид [6].

divB=0; rotH =J= σ(E+uB); B=µH; rotE = - ∂B/∂t;

∂ρ/∂t + div(ρu)=0; P= P(ρ,e); ρ[∂u/∂t+(u ∇ )u]=- ∇ P+F n ; ρde/dt – (P/ρ)(dρ/dt)= j²/σ.

Здесь: E и H – напряженности электрического и магнитно поля, u – массовая скорость, e=e (P, ρ) – внутренняя энергия и уравнение состояния, ρ – плотность, F_n=J*B – пондеромоторная сила на единицу объема . Полученные безразмерные критерии моделирования позволяют пересчитать данные наземных экспериментов и расчетов на разные энергии и высоты .

В модельных исследованиях применялась батареи конденсаторов, удовлетворявшие критериям моделирования с разными параметрами с максимальной емкостью С 0 =13000 мкФ, напряжением U 0 =5 кВ, запасаемой энергией С₀U₀²/2=160 кДж. При разряде конденсаторной батареи через плоский проводник из алюминиевой фольги возникал электрический взрыв, который имитировал световую вспышку молнии и возбуждал УВ. Для моделирования влияния бури на параметры УВ проводился обдув разрядного промежутка со скоростями до 100 м/с.

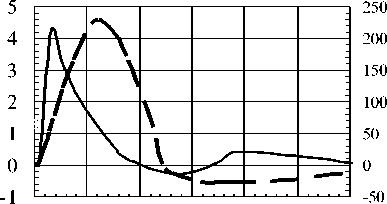
U, кВ                ^а                    I, кА

0     100   200   300   400    500   600

t, мкс

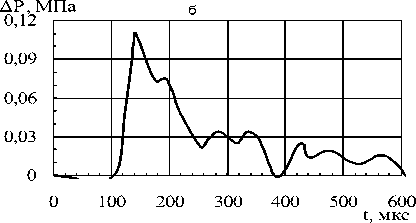
Рис. 1. Экспериментальные зависимости напряжения (линия) и тока (пунктир) разряда – (а). Приращение давления в УВ (б).

Лазерная плазма создавалась облучением преград фотодиссоционными лазерами со взрывной накачкой на длине волны 1.315 мкм в режиме плазмообразова-ния. Применение лазеров позволило более, чем на порядок повысить плотность подводимой энергии q и другие параметры моделирующей плазмы.

Для измерения тока i, напряжения U, длительности t0 и электрической энергии E, выделившейся в разряде применялись пояс Роговского и делитель напряжения. Высокоскоростная фотография, калориметры, фотодиоды, пьезоэлектрические датчики и импульсо-меры применялись при измерении параметров плазмы и УВ [9].

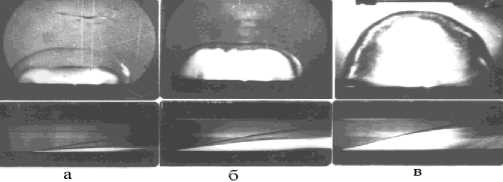
Рис. 2 а, б, в. Фотографии развития разрядного канала и его щелевые развертки у поверхности плоской преграды при плотностях потока q подводимой энергии 0,6; 3; 9 МВт/см ²

Результаты модельных исследований.

На рис. 1 a, b, c показаны характерные временные зависимости напряжения, тока и давления УВ в воздухе при разряде воспроизводящие соответствующие параметры молнии. На рис. 2 а, б, в приведены высокоскоростные фотографии разрядов в режимах лупы времени и щелевой развертки камерой СФР – 2, которые должны воспроизводить параметры молниевой плазмы. С ростом плотности потока подводимой энергии q зона энерговыделения догоняет фронт УВ. При q≈3 МВт/см2 они практически совпадают.

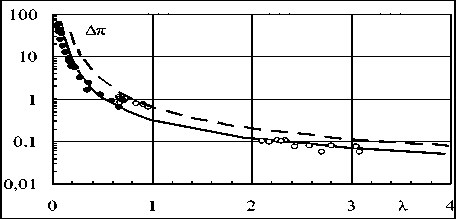
Рис. 3. Зависимости приращения максимального безразмерного давления ∆π в УВ от безразмерного расстояния λ. Пунктир расчеты по формуле Садовского для взрыва тротила, сплошная кривая расчет для взрыва сферы [3], черные и светлые кружки – результаты измерений при лазерном облучении и разрядах .

На рис. 3 в безразмерных переменных принятых для моделирования, черными и светлыми кружками показаны результаты измерений при лазерном облучении и разрядах приращения максимального давления ∆P_m в УВ в виде зависимостей ∆π = ∆P_m/P₀ от безразмерного расстояния λ = R/(E/P₀)^1/3. Сплошными кривыми показаны расчеты [3] для взрыва сферы и пунктиром по формулам Садовского (1) для взрыва сферического заряда тротила [4, 9].

∆Pm= 0,084/(R/G1/3) + 0,27/(R/G1/3)2 + 0,695/(R/G1/3)3, I = 184//(R/G2/3) (1), где давление ∆Pm в МПа, расстояние R в м, G масса тротила в кг, R/G1/3=3,47 λ= 3,47R/(E/P0)1/3. Энергия взрыва тротила принята E=4,2 МДж/кг.

Сравнением результатов измерений с расчетами по формуле Садовского (1) получено среднее значение тротилового эквивалента разряда ТЭ=0,27. Расчеты для взрыва сферы [3] совпадают с опытными данными при электроразряде и облучении, поэтому при определении параметров УВ вызванных импульсом плазмы принималось ТЭ=1.

На рис. 4 а, б точками показаны результаты измерений при разрядах приращения максимального давления ∆P m и удельного импульса I в УВ в зависимости от приведенного расстояния R/G^1/3. Пунктирными и сплошными линиями показаны соответственно расчеты для взрыва горячей сферы [3] и для взрыва сферического заряда тротила [4] по формулам Садовского.

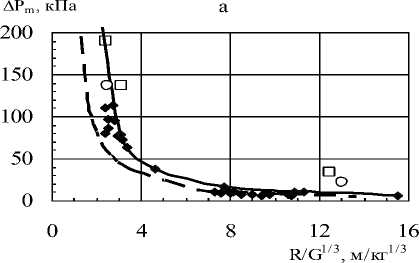
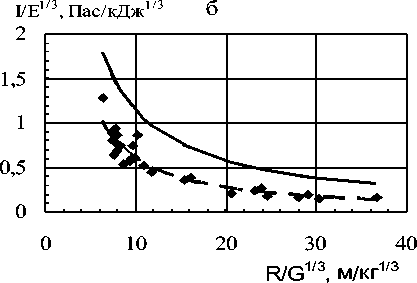
Рис. 4 а, б. Зависимости приращения максимального давления ∆P_m и удельного импульса I/E ^1/3 в УВ при электрическом разряде от приведенного расстояния R/G ^1/3 . Черные точки без продувки, светлые кружки и квадраты скорость продувки 40 и 80% от максимальной. Сплошные и пунктирные кривые – расчеты по формулам Садовского (1) для взрыва тротила и для взрыва горячей сферы .

Сравнением результатов измерений с расчетами по формулам Садовского (1) получены средние значения тротилового эквивалента разряда ТЭ=0,27 и 0,34 для максимального давления и импульса соответственно, а при сравнении с расчетами [4] совпавшими на больших расстояниях с опытными данными ТЭ=1. Измерения параметров УВ при обдуве для моделиро- вания влияния бури на интенсивность грозы показали, что при скоростях обдува выше 100 м/с давление возрастает более, чем вдвое, а ТЭ на порядок.

В табл. 1 приведены измеренные яркостные температуры разряда при разных энерговкладах, характерных для молнии. Определенные по скорости расширения разряда давления ∆P ≈ 5 МПа для УВ и плазмы, на порядок меньшие, чем при взрыве тротила. При лазерном облучении параметры энерго-вклада и плазмы соответствовали приведенным для разряда.

Таблица 1 Зависимость температуры плазмы в разряде от энерговклада

E, кДж	35	27	19	14
T, кK	21	19,5	20	18

Приведенные данные модельных измерений при выполнении условий моделирования соответствуют параметрам молнии и грома [1, 2]. Лидеру с током около 100А при грозе соответствует стадия прогрева проводника до начала электрического взрыва. Токи около 100 кА при электрическом взрыве в разряде соответствуют 2 стадии молнии, когда пробой с высокой скоростью распространяется назад к облаку, выделяется основная энергия и возникает УВ. Температуры разрядной плазмы в таблице 1 и молнии соответствуют при близких значениях удельной мощности энерговклада j2/σ в модели и натуре. Характерные длительность разряда и УВ при моделировании около 1 мс/МДж1/3 близки к длительности грома и молнии.

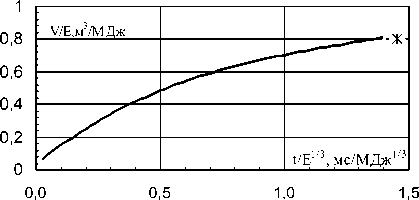
Рис. 5 . Фрагмент фото молнии с экспозицией 13,5 мкс и зависимость приведенного объема изотермы T/T₀ = 10 от приведенного времени для взрыва горячей сферы, крест - приведенный эквивалентный объем молнии V 1 /E = 0,8 м ³ /МДж ³ .

Определение энергии молнии по ее фотографиям. В настоящее время имеется большое количество опубликованных фотографий молний. Обычно, диаметр проводящего канала молнии с температурой около 3 кК достигает до 0,1 м. На рис. 5 приведена фотография с экспозицией 13,5 мкс в конце развития очень большой молнии (когда пробой шел в обратную сторону) из [5] и зависимость приведенного объема V/E от приведенного времени t/E1/3 для изотермы T/T0=10 при взрыве горячей сферы. Крест – приведенный эквивалентный объем молнии V1/E=0,8 м3/МДж, принятый равным максимальному объему изотермы.

На фото рис. 5 указан масштаб, позволивший оценить объем V₁=π R₁²*h=3,8м³ и средний радиус R₁=1,1 м участка молнии высотой h=1 м для цилиндрической симметрии. Для определения энергии молнии сравнивался объем V 1 ее участка высотой 1 м на фотографии и ограниченный изотермой T/T₀ = 10 (T₀=300 К) равный объем продуктов взрыва эквивалентной горячей сферы из расчета [3] с радиусом R₂ = (V 1 /4,18)^1/3=(3,8/4,18)^1/3=0,97 м. Предполагалось, что на фото видна область с температурой свыше 3 кК. Удельная энергия молнии E=V 1 /(V 1 /E) = 3,8/0,8 =4,75 МДж/м. Время от начала разряда t=2,08 мс. Молния с характерной длиной 4 км будет иметь энергию E=4,75*4000=19000 МДж.

Определение параметров УВ при грозах по данным модельных исследований.

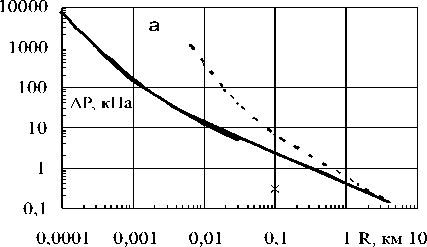
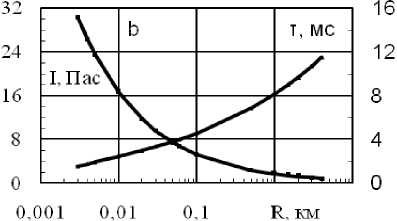
Рис. 6 a,b. Расчетные зависимости приращения максимального давления ∆P, удельного импульса I и длительности τ в УВ от расстояния R по нормали к центру молнии длиной L = 4 км при выделившейся энергии E = 4,2 ГДж.

На рис 6 a,b показаны рассчитанные по разным моделям параметры УВ в воздухе при пробое с энергией E=4,2 ГДж (1000 кг тротила) между 2 облаками при нормальном атмосферном давлении. Пунктир на рис. 6 а – расчет по формуле Садовского (1) для сферического взрыва тротила массой G=270 кг (принималось ТЭ=0,27). Сплошными линиями показаны расчеты для цилиндрического взрыва тротила по эмпириче- ским формулам справедливым в диапазоне 0,035 < ∆Pm < 2,35 МПа [4].

∆P m =1,02(q/R²)+0,2(q^3/8/R^3/4);

I=397(q3/4/R1/2); т=2I/KPm    (2), где R в м, ∆Pm в МПа, I в Пас, q=0,0675 кг/м – удельная масса тротила в кг/м при G=270 кг и длине заряда L = 4 км. Оценки давления УВ при цилиндрической симметрии по данным для взрыва сферы [3] при высоких давлениях в ближней зоне проведены в предположении, что ТЭ=1 и зависимости давления от объема не зависят от симметрии взрыва.

Оценки звуковых и сейсмических сигналов при грозах.

Для о ценки параметров звуковых возмущений на больших расстояниях при ∆ P_m ≤ 10 кПа, где формулы (1, 2) не определены, применялись асимптотические формулы для УВ [Ландау, Лифшиц, 1954]. Коэффициенты в классических формулах получены из формул (1, 2) при ∆ P_m = 10 кПа. Для сферического и цилиндрического взрывов тротила они имеют вид

∆P m =179/(R/G^1/3)(Ln(R/G^1/3))^1/2, I=184(G^2/3)/R, τ=2I/∆P m (3) ∆P m =207(q^0,375/R^0,75), I=397(q^0,75/R ^0,5), t=3,84q^0,375R^0,25    (4)

где ∆P в кПа, I в Пас, R в м, G в кг.

В табл. 2 приведены оценки параметров звуковых возмущений у земли при пробое между двумя облаками на высоте 4 км с энергией E = 4200 МДж по формулам (3) при R=4000 м, G=270 кг для сферического взрыва.

Таблица 2 Параметры звуковых возмущений

∆ P m , Па	I, Па с	τ, мс	∆ P m1 , Па	ит1 , мкм/с
110	1,91	33,5	198	51

При наземных измерениях звуковых и сейсмических сигналов при грозах обычно полоса пропускаемых частот измерительной аппаратуры f ≤ 20 Гц. В табл. 2 временной профиль волны в расчетах считался треугольным, учитывалось удвоение амплитуды давления ∆ P_m при отражении от земли и завал ее фронта измерительным трактом, тогда

∆ P(t) = 2 ∆ P_m (1-t/τ)(1-exp(-2πft)) (5)

При длительности УВ τ=33,5 мс фильтр уменьшал давление на 10%. Максимальное давление в грунте A P_m1 определялась из формул (3, 4). Амплитуды скорости сейсмических колебаний при грозе оценивались по формуле u m1 = 2 ∆ P m1 /cρ при скорости звука c = 2000 м/с и плотности ρ=2000 кг/м³. Значение скорости сейсмических колебаний u m1 = 51 мкм/с значительно больше значения u_m ≈ 5 мкм/с измеренного в [8] при ударе молнии на землю. Рассчитанное значение звукового давления ∆ P_m=110 Па в воздухе также превышает измеренные величины. Выбранная высокая энергия молнии в расчетах 4200 МДж встречается редко. При среднем диаметре молнии около 0,1м [1, 2] и энергии 0,01 МДж/м или 39,2 МДж, что почти в 100 раз меньше принятой в таблице 2 получим ∆P m =20 Па, u_m1=9,5 мкм/с, что можно считать хорошим согласием с опытным значением u m1 =5 мкм/с. Если учесть неоднородность атмосферы, приводящую к снижению параметров УВ то различие с измерениями будет еще меньше.

Выводы. Предложены критерии моделирования молнии и грома мощными электрическими разрядами и импульсами лазерной плазмы на основе общих определяющих модельные и натурные процессы МГД уравнений. По результатам измерений параметров плазмы и УВ определены тротиловые эквиваленты электрических разрядов и импульсов лазерной плазмы, энергия молнии по ее фотографии, параметры УВ с учетом внешнего обдува со скоростями до 100 м/с, моделирующего бурю. Оценены звуковые и сейсмические сигналы на больших расстояниях от грозы.