Моделирование поведения агентов в облаке интернет-обучения

Облачные технологии стали уже общепринятым инструментом работы в Интернет. В основном это относится к организации хранения информации пользователей, и соответственно, доступа к ней, а также простых инструментов по ее обработке. На наш взгляд, наибольший – синергетический – эффект может дать интегрированное использование всех возможностей облачных технологий. Именно такой подход реализуется в интеллектуальной Интернет-платформе ГЕКАДЕМ, которая разрабатывается в Иркутском государственном университете.

1.    Архитектура интернет-платформы

Архитектура интернет-платформы представляет собой интегрированную мультиагентную систему, функционирующую в динамично меняющемся интернет-облаке интеллектуальных ресурсов [1] . Как уже отмечалось, принципиально невозможно обеспечить общее централизованное управление ресурсами облака, поэтому возможным решением может быть самоорганизация как деятельности пользователей, так и функционирования компонентов облака интеллектуальных ресурсов. В основу реализации самоорганизующейся системы интернет-обучения заложен мультиагентный подход. В данной статье будут рассмотрены принципы функционирования двух классов агентов платформы: владельцы ресурсов и пользователи ресурсов. Внутри классов агенты делятся по типам, и соответственно видам [1]. При этом поведение агентов будет определяться логикой, построенной на теории игр, где параметры стратегий игроков (агентов) динамически пересчитываются по сетям доверия в соответствии с байесовским подходом.

Очевидно, что в силу постоянной динамики облака мы не сможем построить сеть доверия «раз и навсегда», нам придется формировать ее всякий раз, когда агенту нужно будет принять решение. Как уже отмечалось [1], в этой ситуации мы будем следовать принципу «локально- сти», т. е. строиться будет фрагмент сети доверия, а точнее, дерево, корнем которого будет объект, для которого ф ормируется оценка. Максимальное количество уровней, по которым будут рассчитываться соответствующие параметры узлов, может быть глобальным параметром платформы, в пределах которого агенты могут выбирать радиус локального окружения.

Рассмотрим подробнее механизм формирования динамический сетей доверия. Для этого сначала следует понять, какова структура облака интеллектуальных ресурсов, т. е. определить множество составляющих и отношений на них. Будем следовать KFS модели представления знаний, в которой базовым элементом является учебный блок

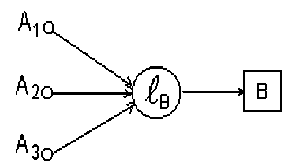
Рис. 1. Учебный блок где

B – результат изучения учебного блока,

A i – входные знания, необходимые при изучении блока.

Блок может состоять из конечного множества других блоков, в этом случае он будет рассматриваться как кластер, в котором единственный выход и четко определены входы, если они есть. В дальнейшем мы будем рассматривать все интеллектуальные ресурсы, как такие кластеры знаний.

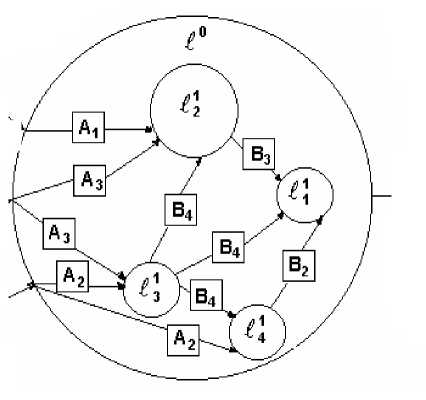
Рис. 2. Кластер знаний

Таким образом, на множестве интеллектуальных ресурсов в соответствии с KFS моделью представления знаний [1] могут быть заданы два базовых отношения строгого частичного порядка:

part(x,y) – объект входит в состав объекта y source(x,y) – знания из объекта x нужны при изучении объекта y.

Очевидно, что эти отношения определяют облако интеллектуальных ресурсов как неоднородную семантическую сеть кластеров, которую можно представить для каждого отношения отдельно в виде ориентированного графа.

Отношение source(x,y) – будет определяющим для агентов – пользователей ресурсов либо при построении траектории учебного процесса, в случае статического планирования, либо при выборе следующего кластера для изучения, в случае планирования с «колес». И в том, и в другом случае алгоритм планирования по заданному графу отношения source (x,y) строит ярусно- параллельную форму (ЯПФ), предложенную Д. А. Поспеловым [2].

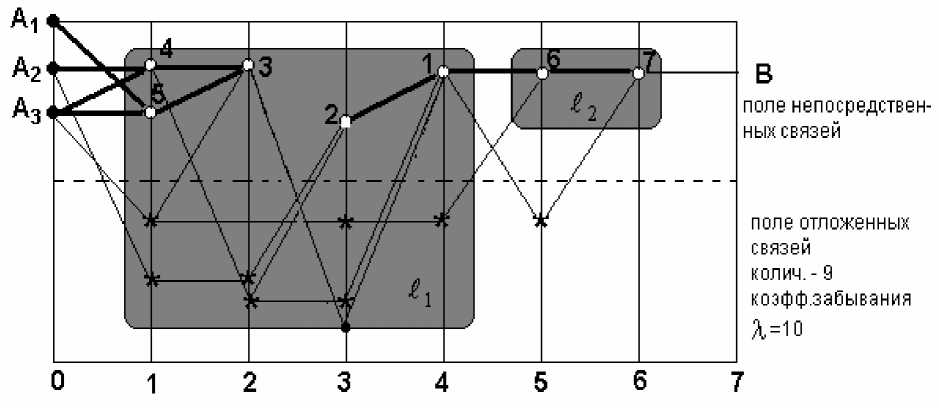
Рис. 3. Ярусно-параллельная форма кластера знаний

В представленном примере видно, что почти в любой точке алгоритма есть альтернативы. Но как обеспечить рациональное поведение агентов? Каким должен быть следующий шаг? Чтобы ответить на этот вопрос, автор использует байесовский подход и теорию игр. Агенты принимают решения на основе анализа текущей ситуации, но при этом работает правило локальности, т.е. для анализа доступен подграф соответствующего графа. При этом отношение part( x,y ) будет служить основой для построения соответствующего фрагмента сети доверия для расчетов вероятностей условных выигрышей.

2.    Моделирование взаимодействия агентов

Рассмотрим взаимодействие представителей двух классов агентов , когда агенту-потребителю нужно получить ресурс. Конечно, реально у каждого игрока может быть много разных стратегий такой сделки, например:

Владелец

• •    продать по фиксированной цене

• •    продать, не дешевле чем min .

• •    продать подороже, но продать

• •    продать по любой цене

• •    при нескольких одновременных запросах и прочих равных условиях продать потребителю определенного типа

• •     …..

Потребитель

• •    купить самый дешевый, если предложений несколько

• •    купить подешевле, но надлежащего качества

• •    купить самое качественное, цена не важна

• •    купить, не дороже чем max

Ситуация, очевидно, весьма неоднозначная и ее можно рассматривать в нескольких аспектах: Для простоты изложения мы не будем вдаваться в детали, хотя, конечно, именно там «кроется дьявол», а рассмотрим последовательно варианты ситуация, в которых агенты могут принимать решения, использую подходящие модели из теории игр [3].

Игра с нулевой суммой

Рассмотрим ситуацию с одним ресурсом и одним претендентом. Для каждого агента определены варианты действий, и известно, что каждый может получить/потерять во всех возможных комбинациях их выбора. Интересы агентов противоположны: выигрыш одного является проигрышем другого. Это классическая антагонистическая игра, или игра с нулевой суммой, которую можно представить в виде платежной матрицы размером m x n , у которой каждая i-я строка ( i=1, 2, .., m ) отождествляется с i-й стратегией первого игрока, а каждый j-й столбец ( j=1, 2, .., n ) отождествляется с j-й стратегией второго игрока. Элементы матрицы носят смысл выигрыша первого игрока (или проигрыша второго).

Пусть платежная матрица игры имеет вид a 11 a 12 "' a 1 n

a 21 a 22 "' a 2 n a , a <••a m1 m2     mn

Понятно, что гарантированный выигрыш игрока при выборе некоторой стратегии равен минимуму соответствующей строки min aij , поэтому в результате он выберет вариант с наи-j большим значением такого минимума

a = max min a,, .

i j ij

Величина α называется нижней ценой игры – это то, что может себе гарантировать первый игрок при максиминной стратегии.

Соответственно, второй игрок может себе гарантировать

в = min max a„ . j                     ij

i

Величина β называется верхней ценой игры. Соответствующая стратегия второго игрока называется минимаксной.

Понятно, что в общем случае α ≤ β , но когда α = β, то мы имеем седловую точку игры, и такое решение является оптимальным для обоих игроков.

Смешанные стратегии

Случаи, когда имеется седловая точка, довольно редки на практике. В этом случае чаще встречаются ситуации, когда седловых точек нет, т. е. нижняя цена игры α строго меньше верхней цены β.

Прежде отметим, что если мы обозначим через V действительную цену игры, то очевидно, что при правильных действиях игроков

α ≤ V≤ β.

К такому компромиссу можно прийти, если такие сделки проводить многократно. И тогда надо менять стратегии агентов таким образом, разделить разность β – α между двумя игроками, чтобы была максимально возможная выгода для каждого.

Процесс чередования стратегий называется смешанной стратегией. Каждый ход в смешанной стратегии – это выбор какой-то определенной стратегии Аi для игрока А и какой-то стратегии Вj для игрока В. Выбор стратегии – это случайный процесс, поэтому каждую выбранную стратегию на каждом шаге мы можем рассматривать как значение случайной величины вероятностью pi для первого агента и, соответственно, qj для второго. Понятно, что p1 + p2 + ..+ pm = 1.

q 1 + q 2 +..+ q n = 1 .

Векторы P ( p1, p2, .., pm), Q (q1, q2, .., qn) представляют смешанную стратегию первого и второго агента, соответственно, а пара (P, Q) называется ситуацией в смешанных стратегиях. В этом случае агенты выбирают стратегии Аi и Вj независимо друг от друга случайным образом. И тогда цена игры первого агента есть математическое ожидание mn

• V XX « j P i q , .

i = 1 j = 1

Ясно, что цель первого агента заключается в максимизации значения V , а цель второго агента заключается в его минимизации Решение можно получить, решая двойственные задачи линейного программирования и доказано, что при отсутствии седловой точки эта задача имеет единственное решение.

Игра с ненулевой суммой

Если величина выигрыша первого игрока не совпадает с величиной проигрыша игрока В, то такой игре соответствуют уже 2 платежные матрицы, а игру называют биматричной. Хотя можно ее представить одной матрицей, где эл ементом является вектор (x,y), где x – выигрыш первого, а y – второго игрока. Каждый агент может выбрать оптимальную с его точки зрения стратегию, используя принцип максимина. В качестве оптимальных стратегий агенты могут также рассматривать те, которые соответствуют равновесию по Нэшу. Но на наш взгляд, как и в случае модели антагонистической игры, лучше перейти к смешанным стратегиям, где векторы вероятностей для каждого игрока можно определить аналогичным способом.

Заключение

Работы агентов по выше представленным моделям поведения опробованы на макетных примерах и дали приемлемые результаты. Понятно, что они далеко не исчерпывают все виды взаимодействий агентов платформы. Например, не рассматривали возможности формирования коалиций со своими интересами. В настоящее время ведутся исследования по привлечению более сложных моделей теории игр для решения таких задач, таких как арбитражная схема Нэша, вектор Шепли для коалиций, построение попарных соответствий (мэтчинга) по Шепли. И это позволяет автору надеяться на полную реализацию платформы облачного интернет-обучения ГЕКАДЕМ, работающей на принципах самообучения и самоорганизации.