Моделирование поверхности строительной конструкции порциями треугольной формы с применением обобщенной линейной интерполяции

При проектировании строительных конструкций со сложной криволинейной формой поверхности часто возникают задачи геометрического моделирования составной поверхности, состоящих из порций треугольной формы. В настоящее время существует достаточно много способов построения поверхностей треугольной формы. При моделировании поверхности, имеющей треугольную область изменения параметров, чаще всего используют барицентрические координаты [1]. Этот способ удобен, как при описании формы поверхности, так и при решении задач строительной механики. В последние годы для усиления несущей способности строительных конструкций стали широко применять полимерные композиционные материалы на основе различных волокон [2]. Использование подобных материалов требует разработки способа, позволяющей описывать, как треугольную ориентацию нитей, волокон, являющихся граничными кривыми треугольной порции поверхности, так и поверхность внутри порции с параметрами граничных кривых. Решению этой задачи посвящена данная статья.

Уравнение треугольной порции поверхности с применением обобщенной линейной интерполяции

Пусть форма поверхности строительной конструкции нам задана. Допустим, что необходимая сетка кривых, определяющих поверхность конструкции, уже построена. Сетка кривых делит поверхность на совокупность треугольных порций, которые ограничены Г (и, 0), Г(0, v) и Г(1, v) кривыми, как показано на рисунке 1. Пусть криволинейные параметры и и v изменяются в пределах от 0 до 1 вдоль соответствующих границ. Задача определения точки внутри треугольной порции поверхности сводится к нахождению функции Г(и, v), которая при u = 0, u = 1, v = 0 представляет нужную граничную кривую, а при v = 1 граничную угловую точку.

Введем кубическую интерполяционную функцию Эрмита на отрезке [0,1] для описания граничных кривых порции поверхности. Сегмент кривой описывается уравнением вида [3].

F (g) = F (0)^( g ) + F (1)« 1 ( g ) + r^ (0)Д( g ) + F'_g (1)Д( g ),                  (1)

где ^(g), tz^ g ), Д( g ), Д( g ) - функции сопряжения;

а о ( g ) = 1"3 g ²+2 g ³;

« 1( g) = 3 g2-2 g3;

Р о⁽ g ^{) =} g ²g g ² + g ³;

Р , ( g ) = -2 g ² + g ³.

' /КОЛ

V      V

HU-O) ■

M 0)'

Рис. 1. Треугольная порция поверхности с параметрами u и v

Используя выражение (1), запишем уравнения для граничных кривых:

r (u ,0) = F (О,О)« о ( u ) + г (1Ж( и ) + ^; (O,O)Z? o ( u ) + F u ' (1,0)Д( u );

r (0, v ) = Г (0,0)« 0 ( v ) + F (0,1)^( v ) + F (0,0)Д,( v ) + F v (0,1)Д( v );

r (1, v ) = F (1,0)^( v ) + F (0,1)^( v ) + r v (1,0)P 0 ( v ) + r v (0,1)Д( v ).

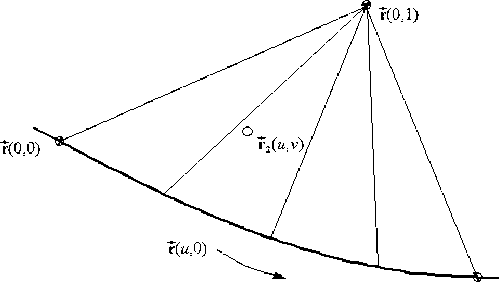
Рассмотрим задачу построения порции поверхности, если заданы только две ее граничные кривые F (0, v ) и F(1, v ). Применяя линейную интерполяцию в и -направлении, получим цилиндрическую поверхность (рис. 2)

^F! ( u , v ) = (1 - u ) ^F (0, v )+ ur (1, v ).                                      (2)

Линейная интерполяция в v -направлении дает коническую поверхность, удовлетворяющую двум другим граничным условиям (рис. 3):

F ( u , v ) = (1 - v ) ^F ( u ,0)+ v ^F (0,1).                                   (3)

Найдем сумму F ( u , v ) и F ( u , v ). С помощью (2) и (3) получим следующее выражение:

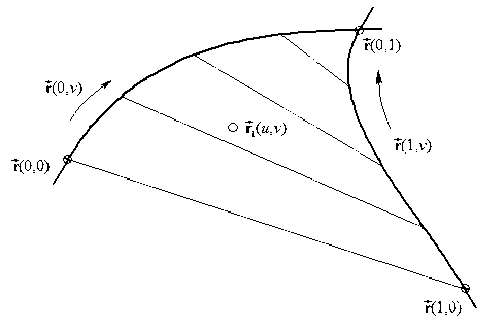
Рис. 2. Порция поверхности, получаемая линейной интерполяцией в u-направлении rx(u, v) = F (u, v) + F (u, v) = (1- u ) F (0, v) + ur (1, v ) + (1- v) r (u ,0) + vr (0,1).            (4)

Последовательно подставляя в выражение (4) u = 0, u = 1, v = 0, v = 1, получим

F 1 (0, v ) = F (0, v ) + (1 - v ) F (0,0) + v F (0,1),

F ¹ (1, v ) = F (1, v ) + (1 - v ) F (1,0) + v F (0,1),                            (5)

F 1 ( u ,0) = (1 - u ) F (0,0) + u F (1,0) + r ( u ,0),

F * ( u ,1) = 2 F (0,1).

Из (5) видно, что сумма выражений F ( u , v ) и f> ( u , v ) не дает требуемой поверхности. Для восстановления первоначальных граничных кривых необходимо из этой суммы вычесть дополнительное слагаемое F ( u , v ). Слагаемое F ( u , v ) можно определить с помощью того же метода интерполяции по двум направлениям при использовании только информации об угловых точках. Для F ( u , v ) имеем следующее выражение:

Fo (u, v) = (1 - v )[(1 - u) F (0,0) + uF (1,0)] + vr (0,1).(6)

Результирующее уравнение имеет вид

F (u, v ) = F1( u, v)-F)( u, v).

После подстановки (4), (6), в выражение (7) и сокращения одинаковых членов полу- чим r (u, v) = (1 - u) r (0, v) + uf (1, v) + (1 - v)[ F (u ,0) - [(1 - u) F (0,0) + uf (1,0)]].(8)

Уравнение (8) удобно представить в матричном виде

^F ( u , v ) = (1 — u

u )

^Л F (0, v )

IF (1, v )

+ (1- v )

^F ( u ,0) — (1 -u

u )

^rF (0,0)\

I F (1,0) J

Поверхность (9) является треугольным аналогом линейной поверхности Кунса [3].

7(1,0)

Рис. 3. Порция поверхности, получаемая линейной интерполяцией в v -направлении

Рассмотрим еще одну треугольную поверхность на трех попарно пересекающих кривых. Во многих случаях для описания положения точки внутри криволинейной треугольной порции удобно, когда каждая граничная кривая имеет свой параметр. На рисунке 4 представлены граничные кривые с криволинейными параметрами u, v и w. Как и в первом случае, параметры u, v и w изменяются в пределах от 0 до 1 вдоль соответствующих границ. Используя рассмотренный выше способ построения треугольной порции поверхности с параметрами u и v, можно получить уравнение для порции с тремя параметрами u, v и w где

F ' ( u , v , w) = (1- u

r ⁰( u , v , w ) = (1 -u

(1 -u

+ (1 - w w )

(1- v

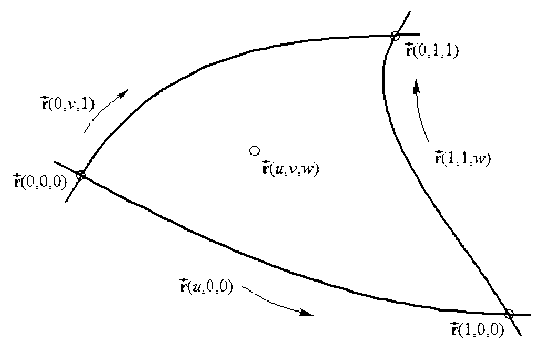
Рис. 4. Треугольная порция поверхности с параметрами u , v и w

r ( u , v , w )

_ F * ( u , v , w)

~    2

r ⁰( u , v , w )

u )

u )

r (0, v ,1) r (1,1, w )

(1- v

(1- w

u )

+ (1- v

( Г (0,0,0)))

w )

r (0,0,0) r (1,0,0) r (0,0,0) r (0,1,1).

r( u ,0,0) r (1,1, w )

+ (1- w

w )

r ( u ,0,0)^

r (0, v ,1) /

Г (0,1,1), ' r (1,0,0) .^r (0,1,1)

•

(1- u

u )

( r (0,0,0)))

+ (1- v

(1- w

w )

r (1,0,0)

' r (1,0,0)

₄ r (0,1,1)

Края поверхности (10) совпадают с кривыми, по которым она построена. При подстановке v = 0 и w = 0 в уравнение (10) получим вектор r (u ,0,0), который описывает участок кривой между точками r (0,0,0) и r (1,0,0). При u =0 и w=1 получим вектор r (0, v,1), который описывает участок кривой между точками r (0,0,0) и r (0,1,1). При u = 1 и v = 1 получим вектор r (1,1, w), который описывает участок кривой между точками r (1,0,0) и r (0,1,1) . На рисунке 5 представлен пример моделирования поверхности порциями треугольной формы, применяемого в строительных конструкциях.

Рис. 5. Поверхность с треугольными порциями

Рассмотренный способ построения поверхности использует треугольную порцию для моделирования поверхностей составной формы строительных конструкций. При описании граничных кривых порции поверхности использовались кубические сплайны в форме Эрмита. Данный способ позволяет описывать поверхность произвольной формы треугольными порциями при задании ее граничных кривых. Его особенностью является определение положения точки внутри порции поверхности при изменении параметров вдоль ее граничных кривых, что позволяет использовать его при решении задач геометрического моделирования строительных конструкций сложных форм с применением полимерных композиционных материалов, имеющих треугольную ячеечную структуру.