Моделирование процесса роста кристаллов сахарозы в сахарсодержащем растворе
Автор: Семенов Е.В., Славянский А.А., Грибкова В.А., Митрошина Д.П., Антипов С.Т.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Процессы и аппараты пищевых производств
Статья в выпуске: 1 (87), 2021 года.
Бесплатный доступ
Кристаллизация сахарозы представляет собой один из наиболее важных этапов в технологическом потоке получения товарного сахара. По своей природе - это развивающийся в достаточно широком температурном диапазоне, условиях изменяющейся концентрации раствора, его пептизации и другого массообменный процесс образования и роста кристаллов сахара в сахарном растворе путем диффузионного переноса в нем молекул сахарозы. К этому нужно добавить еще и такие осложняющие физико-математическую формализацию явления, влияющие на кристаллизацию, как форма кристалла, чистота, вязкостные свойства и поверхностное натяжение раствора, наличие в нем несахаров и т.п. Поэтому среди обусловливающих в целом протекание процесса факторов обычно проводят, сохраняя среди них лишь приоритетные и наиболее важные с позиций исследования. С точки зрения классической диффузионной теории явление кристаллизации трактуется как молекулярный с бесконечной скоростью распространения возмущения от источника диффузионный перенос в растворе молекул сахарозы, вследствие чего концентрация в сахарсодержащей жидкостной системе также полагается изменяющейся мгновенно в каждой точке. Однако, поскольку в реальных условиях этот эффект не наблюдается, то, с целью разрешить это противоречие, вводят понятия возмущенного и невозмущенного, разделенных называемым диффузионным фронтом концентрации областей этих фазовых состояний. Используя кинематические характеристики фронта, определяют время протекания процесса кристаллизации в целом по обеим фазам. Что позволяет с большей, по сравнению с полученными на базе классической теорией результатами, точностью рассчитать период обработки раствора.
Вакуум-аппарат, концентрация раствора, затравка, кинетика кристаллизации, сахароза
Короткий адрес: https://sciup.org/140257366
IDR: 140257366 | УДК: 664.1.054 | DOI: 10.20914/2310-1202-2021-1-62-70
Текст научной статьи Моделирование процесса роста кристаллов сахарозы в сахарсодержащем растворе
This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License
Семенов Е.В. и др.Вестник ВГУИТ, 2021, Т. 83, №. 1, С. 62-70 Введение
Хотя в настоящее время известно четыре научные гипотезы кристаллизации сахарозы, в число которых входит термодинамическая, диффузионная, молекулярно-кинетическая и дислокационная, по нашему мнению, наиболее простой и эффективной для прогнозирования протекания процесса кристаллизации является диффузионная гипотеза П.М. Силина [1–6]. В ней кристаллизация определяется как двухстадийное физическое явление: сначала инициация в чистом сахарсодержащем растворе в виде центров кристаллизации (первая стадия процесса), затем их эволюция – рост кристаллов (вторая стадия). По завершении интродукции в пересыщенный раствор затравочного материала, представляющего собой первую стадию процесса, сам процесс кристаллизации (вторая стадия) осуществляется при температуре Т > 50 °С в условиях градиента концентрации сахарозы в растворе на границе раздела фаз: “жидкость (раствор сахарозы) + твердое (кристалл)”, когда молекулы сахарозы адсорбируются на поверхности кристалла и встраиваются в кристаллическую решетку.
Следует отметить, что современная диффузионная теория процесса кристаллизации не учитывает влияния формы кристаллов на динамику кристаллообразования. Авторы статьи считают наиболее близкой к истине концепцию П.М. Силина [1], полагавшего, что на 1 м2 поверхности кристаллов конденсируется одинаковое количество сахара независимо от их размера.
Стоит обратить внимание на то, что в процессе кристаллизации условия роста кристаллов изменяются беспрерывно. Так, уменьшение объема и толщины слоя межкристального пространства, а также его концентрации наблюдается при росте размеров кристаллов. Помимо этого, вследствие имеющего место возрастания температуры в вакуум-аппарате в результате конденсации, интенсифицируется и собственно диффузионный перенос молекул сахарозы к поверхности кристалла.
Обзор посвященных научно-техническому обоснованию проблемы кристаллообразования сахарозы в вакуум-аппарате зарубежных литературных источников, с одной стороны, показывает, что по-прежнему, усилия специалистов-сахарников в большой степени направлены на изучение традиционной для сахарного производства задачи количественного анализа, в условиях изменения размера кристалла, процесса кристаллообразования в вакуум-аппарате. Так, работы [8, 9] посвящены оценке кинетики кристаллизации сахарозы на основе полученных в кристаллизаторах опытных данных при равномерно-монотонном убывании температуры раствора. Для чего при измерении размера кристалла был применен оптический микроскоп совместно со сканирующим электронным микроскопом типа SEM. При этом рассчитанные результаты сравниваются с полученными в других работах данными.
С другой стороны, особенность литературных источников, с очевидностью, указывает на ускорение перехода научного сообщества в области сахарного производства к использованию в исследованиях углубленного научного анализа, основанного на проведении опытов с использованием новейших образцов в области экспериментального оборудования [10–20]. Это связано с тем, что на практике в растворах, в том числе, и сахарсодержащих, явление кристаллообразования часто протекает в условиях, при которых, увеличивая свой размер, кристалл по габитусу отклоняется от своей классической формы в чистом растворе, т. е. становится дефектообразным. Данный фактор во многих исследованиях служит предметом пристального внимания ученых. Причем, поскольку этот процесс может инициироваться и выступающими в качестве центров кристаллизации имеющими размеры порядка одного нанометра молекулами сахарозы, то в статьях [10, 11] были изучены темпы роста кристаллизации сахарозы в чистых растворах при температуре в кристаллизаторе 313 К и пересыщении 0,094–0,181. При этом полученный кинетический коэффициент (коэффициент диффузии) изменился при начальном перенасыщении с D = 2,79× 10–7 до конечного D = 9,45х10-5 м2/с, соответствующий размер кристалла варьировался от 1,46 ×10–9до7,47× 10–9 м.
С теоретической позиции концепция трактовки явления кристаллизации, в том числе, и сахарозы как молекулярного диффузионного переноса массы (или, аналогично, явления переноса тепловой энергии в классической теории теплопроводности) скорость распространения возмущения от источника массы или энергии принимается бесконечной, вследствие чего концентрация раствора или температура среды изменяются мгновенно в каждой его точке. Чтобы учесть этот фактор вводят понятие «диффузионного фронта» х =р( t ) (рисунок 1). При этом для раствора на фронте осуществляются условия:
-
1) концентрация с равна концентрации невозмущенной области;
-
2) производная дс/дх на фронте полагается равной нулю, что влечет за собой плавное непрерывное распределение концентрации, а также потока концентрации в возмущенной области и во всей исследуемой области.
Принятые допущения означают, что процесс распространения концентрации осуществляется в две фазы.
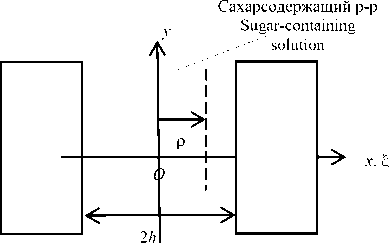
Рисунок 1. Схема к расчету процесса кристаллизации сахарозы в вакуум-аппарате

Кристалл сахарозы | Sucrosecrystal
Ниже, согласно предложенной П.М. Силиным диффузионной модели, с учетом перечисленных особенностей кинетики кристаллообразования в условиях молекулярной конденсации, проводится аналитический и численный анализ процесса кристаллизации сахарозы в вакуум-аппарате.
Постановка задачи
Ставится задача: при заданных геометрических и физико-механических параметрах процесса кристаллообразования получить, с учетом фактора наличия фронта концентрации, количественную оценку по времени эволюции роста размера кристаллов сахарозы, их объемного содержания при обессахаривании межкристального раствора в вакуум-аппарате.
Предварительно, с целью обосновать среднее значение h расстояния между частицами сахарозы исходя из величины объемной концентрации их в растворе принимается, что если V чс и V ут – соответственно, общий объем кристаллов и объем утфеля в вакуум-аппарате, η – объемная концентрация кристаллов в томже объеме, то в соответствии с принятой геометрической моделью жидкостной системы половина расстояния h между двумя соседними частицами составит [6]
h = 5 /(2пт), 0 < П < 1, (1) где η= V чс / V ут , δ – приведенный диаметр частицы сахарозы.
Считают, что массоперенос к частице из жидкой среды осуществляется симметрично и, кроме того, для выбранной расчетной модели с удовлетворительной точностью выполняются все предположения относительно физикомеханических свойств исследуемого объекта.
Поток концентрации q (объем вещества, отводимого с единицы поверхности в единицу времени) целевой субстанции (сахарозы) в направлении оси x в принятой одномерной модели массопереноса рассчитывают по формуле согласно первому закону Фика
∂с q = -D
∂ х
где D – коэффициент диффузии, с – объемная концентрация сахарозы.
При формализации физической модели предполагают, что концентрация сахарозы в исходном растворе одинакова по всему объему, центры кристаллизации распределены равномерно, кристаллы в процессе своего роста имеют форму, близкую прямоугольному параллелепипеду и сохраняют приблизительно схожие размеры. Кроме того, дополнительно считают, что начальный пересыщенный объем раствора включает как центры кристаллизации, достаточно большое количество молекул и частиц этого продукта настолько малым размером, что эти частицы диффундировали к поверхности кристалла и впоследствии встраивались в кристаллическую решетку.
В дальнейшем полагают, что процесс кристаллообразования сахарозы обусловлен ростом кристалла лишь в направлении большей из его граней, то есть, в направлении оси x . Тогда в качестве приближенной геометрической модели кристалла принимается полупространство x > h , ограниченное поверхностью x = h , к которому из области 0 ≤x ≤ h раствора диффундируют молекулы данного вещества (рисунок 1).
Более того, считают, что исследуемый процесс развивается, если концентрация сахарозы превышает растворимость ее или так называемую равновесную концентрацию, т. е. при наличии разницы в концентрации растворенного вещества в пересыщенном растворе.
Тогда с целью количественного анализа задачи о росте кристалла в соответствии с законом сохранения массы приходят к кинетическому уравнению [1]
д с _ д2 c
== г. , д t дx2
uде t – время, D – полагаемый постоянной величиной коэффициент диффузии.
В таком случае, если с п – исходная концентрация сахарозы в пересыщенном растворе, то решение уравнения (3) согласуют с начальным условием
с ( x, 0) = с п =const, 0 < x < h . (4)
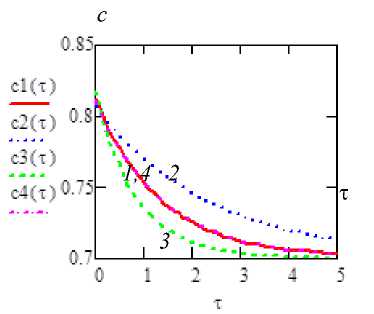
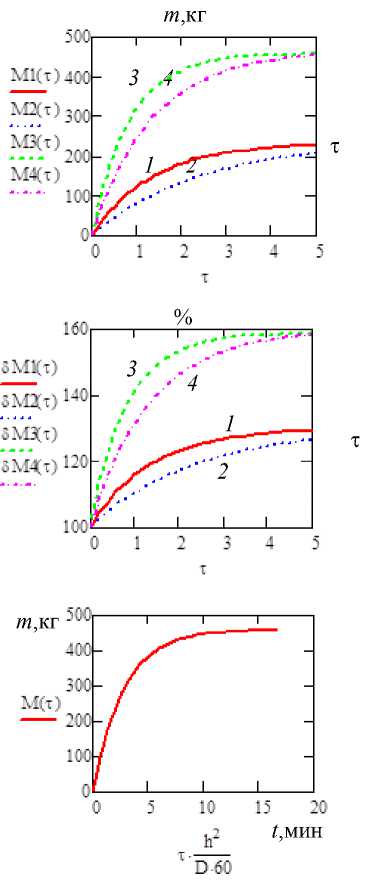
В свою очередь, поскольку посередине расстояния x = 0 между двумя соседними кристаллами концентрация раствора сахарозы достигает максимальное значение, то граничное условие имеет форму дс(0, t) _ „ v , = 0,0 ∂x В соответствии с концепцией Л.П. Хворо-вой и В.А. Коваленко [4, 5] через определенный промежуток времени по мере роста кристалла в растворе в контактирующем с поверхностью кристалла слое раствора скорость осаждения вещества определяется законом (2), что согласуется с представлением о наличии в растворе фронта концентрации. Тогда граничное условие на границе раздела раствор-кристалл x = 0 имеет следующий вид дс(0, t) г .. . —---= Y[c(0,t) - сн] ∂x или(6) дс(0, t) —---= а[c(0,t) - сн] ∂x где a =y/D, Y — так называемый коэффициент кристаллохимической реакции, характеризующий скорость поверхностных процессов, м/с, a - удельный коэффициент диффузии, м-1, сн -концентрация насыщенного раствора сахарозы вблизи кристалла. Решение задачи В дальнейшем, с целью упрощения проводимого исследования вводят безразмерные величины по зависимостям с- с xDt —— = и, 7= 5 , А с hh γh ah = D = Т Аc = сн - сп <10 где т - аналог числа Фурье (диффузионный), о - аналог числа Био(диффузионный). В таком случае задача (3)-(6) примет форму — /и, (8) дт д^^ v ’ и (5,0) = 0, (9) жо = 0>д5 (10) ди (1, t) .. . -------- + сти (1, t) = ст. ∂ξ (11) Прибегая к так называемому методу осреднения, при исследовании задачи с учетом наличия фронта концентрации, решают ее по двум фазам, заменяя левую часть уравнения (8) ее осредненным значением по интервалу (р, 1), а именно, вводят в рассмотрение функцию [7] 1 1 ди 2ф(в)(т)= ----J — d5, 02) 1 - РР дт где в - индекс фазы (в = 1,2);р - безразмерная координата фронта концентрации. Тогда вместо уравнения (8) используют приближенное соотношение д2 и(1) д5 = 2ф(1)(т), удовлетворяющее, согласно (8)-(11) условиям и (1)(р,т) = 0,(14) [диWfeT) дг] р = 0,(15) [ди (1)(^,т) /д£ + о и (1)(^,т)]^ =1 =о,(16) и, кроме того, вытекающему из (12) равенству 2ф(1)(т) = -^j ^Ц- d5.(17) 1 — Рр дт Проводя последовательно интегрирование в (13), имеют ди(1)(^,т) /д^ = 2ф(1)(т)^ +А1,(18) и (1)(^,т) =ф(1)(т^2 +А1^ +В1.(19) Согласуя (15)-(17) с условиями (14)-(16), для определения неизвестных ф(1)(т), А1, В1, с использованием (18), (19), получают систему алгебраических уравнений (о + 2)ф(1) + (о + 1) А1 + оВ1 =о,(20) р2ф(1) + рА1 + В1 = 0,2рф(1) + А1 = 0,(21) решением (20) является ф(1)(т) =о/D1, А1 =-2ор/D1, В1 =ор2/D1, (22) где обозначено D1 =о(1 - р)2 + 2 (1- р).(23) Подставляя (21) в (19), находят и(1)(^,т) =о(^ - р)2/D1. Функция р =р(т) определяется с помощью (17) Поскольку, согласно (23) ^Ц- = - -^2 dp[2D1(5 - Р) + ^51(5 - Р )2], ∂τ D dτ dρ то после подстановки в уравнение (17) значения ф(1)(т) и значения ди(1)/дт, получают D1(1 — P) = = — dP [2 DJ^f—р) df + dD^f—p )2 df], dT p dp)p откуда, после интегрирования 6 D1(1 — p) = —(1 — p )2dP [3 D1 + (1 — p) DA. dT dp Поэтому с учетом (22) имеют dDL = — 2[а(1 — p) + 1], d p Интегрируя, последовательно, по ξ уравнение (28), имеют: 5и^т) /5^ =2ф(2|(т)^+А2(т),(32) и ^т) =ф(2)(т)^2 +А 2^ +В 2.(33) Поскольку из выражений (30), (32) вытекает, что А2(т) = 0, то в таком случае согласно (33) получают и ^т) =ф(2|(т)^2+В 2.(34) 3 D1 + (1 — p) dD = 7(1 — p )2 + 4(1 — p). d р В результаты чего приходят к дифференциальному уравнению относительно р =р(т) 67(1 — Р) + 21 = — (1 — р) ~ 1^(1 — р) + 4], dT или, после разделения переменных к соотношению (1 — р )7(1 — р) + 4] dt =--dp. (24) 67 (1 — р) + 2] 7 Поскольку выполняется начальное условие т = 0 при р = 1, то интегрируя это выражение слева по т от нуля до т, справа - по р от р до единицы, исходя из (24), т. е., выполняя процедуру Удовлетворяя условию (31), имеют 2ф(2)(т) + о[ф(2)(т) + В2] =о, откуда находят В2 = 1 - (о + 2)ф(2)(т)/о. В таком случае (34) принимает вид и^j) = 1 - ф(2)(т) [(о + 2) /о - Й. (35) Функция ф(2)(т) определяется на основе условий (27), (29), с учетом того, что, с одной стороны,5и(2)(1,т) /5т = -5ф(2|(т)/5т•[(о + 2)/о -с2], с другой стороны p (t )=-1 d-Ф2- i< 2 dT 7 + 2 — т 1(1 — p)[7 (1 — p) + 4] J, 6[а(1 — p) + 2] , получают частное решение (1 — p)2 (1 — р) т =--1-- — f2) df = — 1 d^(2)2а + 6 • 3а Ль [1+р1^ 3ст2 I 2 Продолжительность первой фазы находят путем подстановки р =0 в (25) 1 1 Т1 =— + — 12 3о Т2"^ )■ (26) Если (численным путем) разрешить (25) относительно р как неявную функцию, то тем самым определяют Р =р(т). Вторая фаза. по соотношению и фронт концентрации Функцию ф(2)(т) вводят 1 5 (2) 2ф<2|(т) -J u df J от 0 T L Задача ставится таким образом, чтобы по- лучить решение уравнения 52uи , ,,v ' ^Г = W). удовлетворяющее условиям: и(2)(0,Т1) = 0, 5и(2)(0,т) /5^ = 0, 5и(2)(1,т) /5^ + о и(2)(1,т) =о, 6 dT , и поэтому, разделяя далее переменные в этом уравнении и интегрируя полученное в результате соотношение, находят общее решение ф(2)(т) =D2ехр [-3от/(о +3)], где D2 - произвольная постоянная. Тогда в соответствии с (35) и(2)(f, t ) = 1- D2f 7+2 I 7 — f2 Iехр —3s(t-tx) . (s + 3) , (36) где т1определяют по (26). Далее, принимая во внимание (29), находят D2 =о/(о + 2) ехр [3от1 /(о +3)]. После чего, подставляя D2 в (36), окончательно получают и(2) (f, t) = 1- s (s+2) —3 s (t - tx) . (s+ 3) Таким образом, в рамках принятой физикоматематической модели задача об определении поля концентрации сахарозы в области между двумя смежными кристаллами сахарозы в вакуум-аппарате решена полностью. В дальнейшем, возвращаясь согласно (7) к исходному значению с концентрации сахарозы в сахарсодержащем растворе, имеют с (^,т) = сп+ и(2|(^,т)Лс, (38) где и(2)(^,т) определяется по соотношению (37). Для того чтобы рассчитать эффективность процесса кристаллизации сахарозы, предварительно, на базе зависимости (2), (37) определяется поток q концентрации. При этом, поскольку в соответствии с (37), (38) имеют дс дu(2) . 2ос -Ac -3 s (t -t.) — =--Ac = — --ехр — д^ д^ о + 2 [_ (s + 3) или, согласно (7), в размерных переменных — =----, м-1, (40) то в соответствии с (2), (40) дх h 6^ справедлива формула q = D дс/дх. Поэтому поток q концентрации на поверхности x =h(ξ = 1), в явной форме выражается в виде 2оАcD -3s (t -t1) q =------ехр — (o + 2) h (s + 3) В свою очередь, так как за время dт на той же поверхности осаждается объем сахарозы qh2 dt 2оА ch dQ = = ехр D (о + 2) -3о (г - г1) (о + 3) dt то количество А Vсахарозы, оседающей за период времени т получают, интегрируя выражение (41) в пределах от 0 до т. В результате имеют Q (t, A, h) = А V 2оАch г = ехр (о + 2) J р -3о (г - г1) (о + 3) dr = 2(о + 3) h А c = —--------ехр 3 3(о + 2) Р^ или по массе о (г1 - г) (о + 3) _ ог - exp 3 , . L (о + 3) Q(т, D, h) = Q(т, D, h)xpi, кг/м2, где pi - плотность сахарозы. , м3/м2 Пусть в одном кубометре утфеля содержится, в равных объемных долях п, кристаллы сахарозы размером 8 =10-4 м и межкристального раствора коэффициентами, соответственно, пересыщения сп = 0,8 и насыщения сн = 0,7. И пусть, по соглашению, коэффициент кристаллохимической реакции у = 10-6 м2/с [4, 5], коэффициент диффузии раствора De [10-10,5x10-11], м2/с [2]. Требуется на базе выбранных геометрических и физических параметров процесса определить по массе отнесенный к 1 м3утфеля полный молекулярный расход межкристального раствора в зависимости от времени проведения процесса кристаллизации. Предварительно, поскольку, согласно формуле (1) при п = 0,5 половина расстояния между частицами сахарозы составляет h = 6,3 х10-5 м, то в расчетах принимали he[5x10-5; 10-4], м. В свою очередь, так как количество частиц сахарозы равно пх6/(п83), то их общая поверхность S составляет S = 3/8 = 3х104 1/м3. С учетом (38) на рисунок 2 представлены графики зависимости концентрации сахарозы на середине расстояния между двумя смежными частицами (т. е. при x = 0) Как следует из анализа поведения кривых (рисунок 2), к моменту т = 5 концентрация сахарозы посередине между двумя кристаллами в результате конденсации молекул сахарозы на кристаллах примерно выравнивается, приближаясь к значению сн = 1,1 насыщения. Рисунок 2. Зависимости концентрации сахарозы между двумя смежными частицами от безразмерного времени т процесса обработки центров кристаллизации в сахарсодержащем растворе при различных значениях коэффициента D диффузии и половины расстояния h между кристаллами (h = 5х10-5 м: 1 - D = 5х10-11, 2 - D =10-10 м2/с; h = 10-4 м: 3 - D = 5х10-11, 4 – D = 10-10 м2/с) Figure 2. Dependences of the concentration of saccharose between two adjacent particles on the dimensionless time treatments of the processing of crystallization centers in a sugar-containing solution at different values of the diffusion coefficient D and half the distance h between crystals (h = 5х10-5 m: 1 - D = 5х10-11,2 -D = 5х10-10 m2/s; h =10-4 m: 3 - D = 5х10-11,4 - D = 5х10-10 m2/s) Рисунок 3. Зависимости от временит массы m конденсированной на поверхности кристалла сахарозы при различных значениях коэффициента D диффузиии половины расстояния h между кристаллами (h = 5x10-5 м: 1 - D = 5х10-11, 2 - D = 10-10 м2/с; h = 10-4 м: 3 - D = 5х10-11, 4 - D = 10-10 м2/с) Figure 3. Time т dependences of the mass m of sucrose condensed on the surface of the crystal at different values of the coefficient D diffusion and half distance h between crystals (h = 5х10-5 m: 1 - D = 5х10-11 m2/s, 2 - D = 10-10 /с; h = 10-4 м: 3 - D = 5x 10-11,4 - D = 10-10 m2/s) Рисунок 4. Зависимости от времени т относительной массы 5m/mо, % конденсированной на поверхности кристалла сахарозы при различных значениях коэффициента D диффузии и половины расстояния h между кристаллами (h = 5х10-5 м: 1 - D = 5х10-11, 2 - D = 10-10 м2/с; h = 10-4 м: 3 - D = 5х10-11, 4 - D = 10-10 м2/с) Figure 4. Time т dependences of the relative mass 5m/m0, % of sucrose condensed on the surface of the crystal for different values of the diffusion coefficient D and half the distance h between the crystals (h = 5х10-5 m: 1 - D = 5х10-11, 2 - D = 10-10 m2/с; h = 10-4 м: 3 - D = 5х10-11, 4 – D = 10-10 m2/s) Рисунок 5. Зависимость от времени массы осадившейся на поверхности взвеси из кристаллов сахарозы Figure 5. Time dependence of the mass of a suspension of sucrose crystals deposited on the surface Отраженные графиками рисунок 3, 4 результаты вычислений на базе (42) обнаруживают согласованность полученных результатов количественного моделирования исследуемого процесса с физическим смыслом задачи. А именно, с одной стороны, обессахарива-ние раствора по массе в связи с кристаллизацией сахарозы, как по абсолютному (рисунок 3), так и относительному к исходному (рисунок 4) значениям, по прошествии времени экспоненциально возрастает, и тем больше, чем выше значение коэффициента диффузии (например, на рисунок 3, кривая 2 расположена выше кривой 1). С другой стороны, аналогичным образом, графически, например, рисунком 4 отражена зависимость прироста массы от времени: при коэффициенте диффузии D = 5х 10-11 м2/с, с увеличением расстояния h (и, следовательно, с уменьшением счетной концентрация частиц в растворе), интенсивность процесса кристаллизации снижается – кривая 3 ниже кривой 1. Если, при тех же исходных данных по параметрам процесса расчет проводится в реальном временном режиме, то в таком случае, например, при значениях параметров h = 10-4 м и D = 5х10-11 м2/с графическая зависимость от времени t массы m осадившейся на поверхности взвеси из кристаллов сахарозы в вакуум-аппарате имеет показанный на рисунок 5 вид. Как видно по рисунок 5, процесс кристаллизации завершается практически к пятнадцатой минуте и для возобновления его необходимо раствор “раскачивать”, обогащая его пресыщенной сахарсодержащей субстанцией. Однако следует отметить, что отраженные рисунками 2–5 результаты расчетов, из-за того в них не учитывается эффект истощения раствора сахарозой (в частности, коэффициент А = сн - сп полагается постоянной величиной), приводят к завышенным, по сравнению с наблюдаемыми на практике, данными. Семенов Е.В. и др.Вестник ВГУИТ, 2021, Т. 83, №. 1, С. 62-70 Заключение На основе модели диффузионного массо-переноса целевого продукта, такого как сахароза, из пересыщенного межкристального раствора к кристаллу сахарозы, основанного на уравнении нестационарной диффузии (второго закона Фика), обосновывается физико-математическая модель по прогнозированию протекания процесса кристаллизации сахарозы в данном растворе при учете кинетики фронта концентрации. Предлагается аналитический аппарат для расчета зависимости массы целевого продукта от времени в результате процесса кристаллизации. На основе разработанного аналитического аппарата проводится количественное моделирование эффективности данного процесса.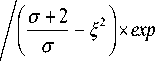
Список литературы Моделирование процесса роста кристаллов сахарозы в сахарсодержащем растворе
- Силин П. М. Технология сахара. Рипол Классик, 2013.
- Магомедов М. Г. Технология получения пасты из сахарной свеклы //Вестник ВГУИТ. 2015. № 3. С. 138-141. doi: 10.20914/2310-1202-2014-3-138-141
- Славянский А.А., Семенов Е., Лебедева Н., Неделькин В. и др. Математическое моделирование кинетики кристаллизации гидратной глюкозы // Сахар. 2014. № 5. С. 45-49.
- Хворова JI.C. Трехпродуктовая технологическая схема получения глюкозы с кристаллизацией двух продуктов в ангидридной форме // Пищевая промышленность. 2017. № 9.
- Хворова JI.C., Баранова JI.B., ГоменюкВ.А. Способ получения кристаллической ангидридной глюкозы. 2018.
- Семенов Е.В., Славянский А.А. Моделирование процесса кристаллизации и центрифугирования. М.: Спутник+, 2015. 217 с.
- Кулинченко В.Р., Мирончук В.Г. Промышленная кристаллизация сахаристых веществ. 2012.
- Berzi К., Suryanarayanan R. Compression-induced crystallization in sucrose-polyvinylpyrrolidone amorphous solid dispersions//Crystal Growth & Design. 2018. V. 18. №2. P. 839-848. doi: 10.1021/acs.cgd.7b01305
- Hubbes S.S., Braun A., Foerst P. Sugar particles and their role in crystallization kinetics and structural properties in fats used for nougat creme production // Journal of Food Engineering. 2020. V. 287. P. 110130. doi: 10.1016/j.jfoodeng.2020.110130
- Velazquez-Camilo O., Bolanos-Reynoso E., Rodriguez E., Alvarez-Ramirez J. Characterization of cane sugar crystallization using image fractal analysis // Journal of Food Engineering. 2010. P. 77-84. doi: 10.1016/j.jfoodeng.2010.03.030
- Khaddour I., Bento L., Ferreira A., Rocha F. Kinetics and thermodynamics of sucrose crystallization from pure solution at different initial supersaturations // Surface Science. 2010. P. 1208-1214. doi: 10.1016/j.susc"2010.04.005
- Frenzel S. Crystallization Schemes in the Sugar Industry// ChemBioEng Rev. 2020. №5. P. 1-9. doi: 10.1002/cben.202000010
- Thakral S., Sonje J., SuryanarayananR. Anomalous behavior of mannitol hemihydrate: Implications on sucrose crystallization in colyophilized systems // International journal of pharmaceutics.2020. V. 587. P. 119629. doi: 10.1016/j.ijpharm.2020.119629
- de Castro B. J. C. et al. Sucrose crystallization: modeling and evaluation of production responses to typical process fluctuations //Brazilian Journal of Chemical Engineering" 2019. V. 36. № 3. P. 1237-1253. doi: 10.1590/0104-6632.20190363s20180240
- SinghK, Gupta S.P., Kumar A., Kumar A. The effect of high intensity ultrasound (HIU) on the kinetics of ciystallizationof sucrose: Elimination of latent period//Ultrasonics sonochemistiy. 2019. V. 52. P. 19-24. doi: 10.1016/j.ultsonch.2018.05.030
- Chakir A., Romane A., Marcazzan G.L., Ferrazzi P. Physicochemical properties of some honeys produced from different plants in Morocco // Arabian Journal of Chemistry. 2016. V. 9. P. S946-S954. doi: 10.1016/j.arabjc.2011.10.013
- Nayik G.A., Dar B.N., Nanda V. Physico-chemical, rheological and sugar profile of different unifloial honeys from Kashmir valley of India// Arabian Journal of Chemistry. 2019. V. 12. № 8. P. 3151-3162. doi: 10.1016/j.arabjc.2015.08.017
- Batal H., Hasib A., Ouatmane A., Dehbi F. et al. Sugar composition and yield of syrup production from the pulp of Moroccan carob pods (Ceratonia siliqua L.) // Arabian Journal of Chemistry. 2016. V. 9. P. S955-S959. doi: 10.1016/j.arabjc.2011.10.012
- Boussaid A., Chouaibi M., Rezig L., Hellal R. et al. Physicochemical and bioactive properties of six honey samples from various floral origins from Tunisia // Arabian journal of chemistry. 2018. V. 11. № 2. P. 265-274. doi: 10.1016/j.arabjc.2014.08.011
- Torr6nen R., Hellstrom J., Mattila P., Kilpi K. Postprandial glycaemic response to berry nectars containing inverted sucrose // Journal of nutritional science. 2017. V. 6. doi: 10.1017/jns.2016.44


